Введение в основы глубокого обучения. Часть 4. Введение в функции активации: tanh, сигмоид, ReLU, PReLU, ELU, softplus, softmax, swish и т. д.

1. Функция активации

• функция активациидаискусственная нейронная сетьизчрезвычайно важныйизособенность；
• функция активации决定一个神经元дадолжен быть активирован,Активация представляет собой то, что нейрон получает информацию и связан с данной информацией;
• Функция активации выполняет нелинейное преобразование входной информации.,Затем конвертируйтеиз Выходная информациякак Входная информация передается следующему слою нейронов.。

Роль функции активации

Если функция активации не используется, выходные данные каждого слоя являются линейной функцией входных данных верхнего слоя. Независимо от того, сколько слоев имеет нейронная сеть, конечный результат представляет собой линейную комбинацию входных данных. Функция активации вводит в нейроны нелинейные факторы, позволяя нейронной сети произвольно аппроксимировать любую нелинейную функцию.。

2. Знакомство с распространенными типами функций активации.

2.1 sigmoid

Определение функции:

$f(x)=\sigma(x)=\dfrac{1}{1+e^{-x}}\quad\text{}$

Производная:

$f^{'}(x)=f(x)(1-f(x))$

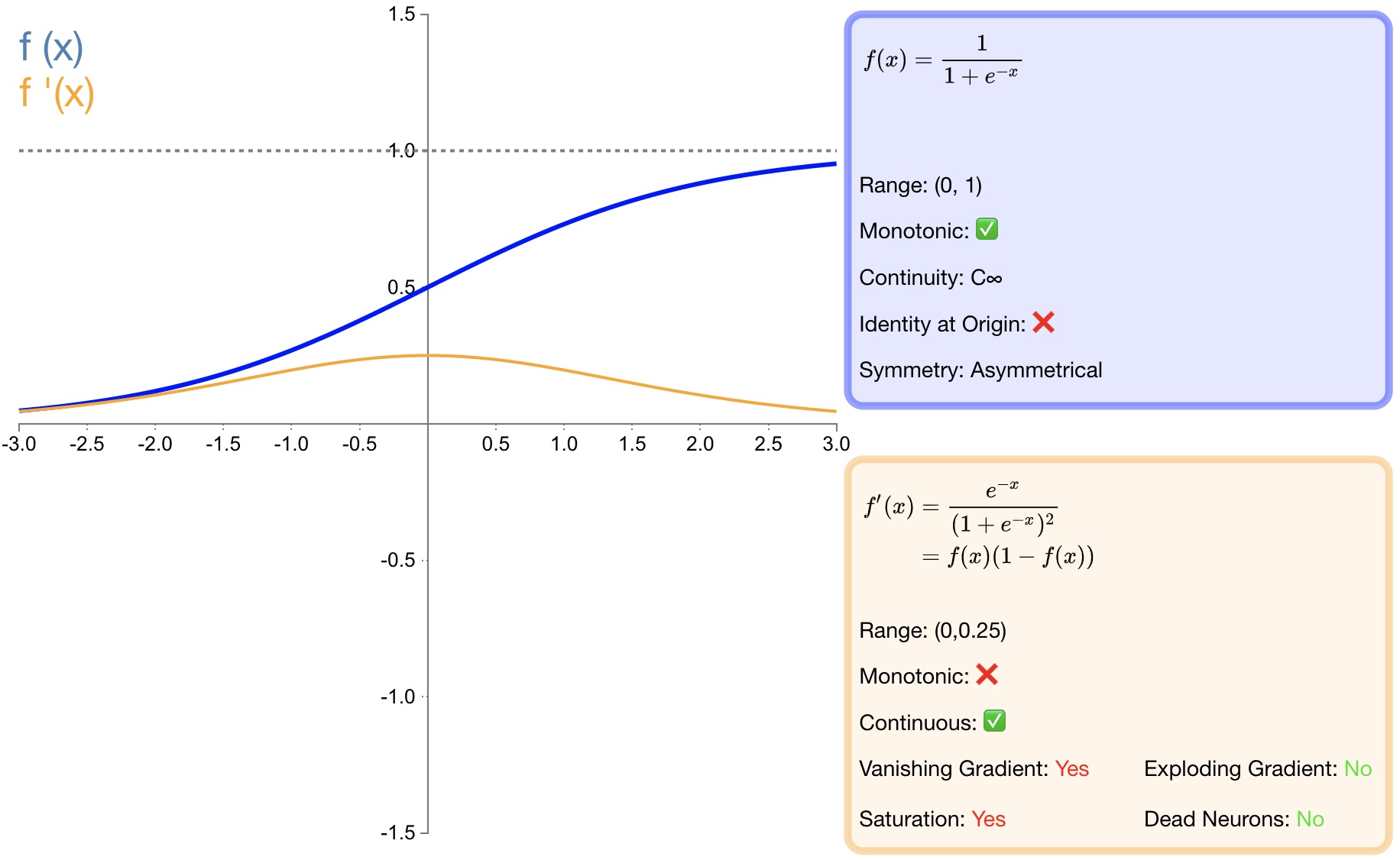
• преимущество:

* Функция $sigmoid$ из вывода, отображенного в между (0,1),монотонный непрерывный,Выходной диапазон ограничен,Оптимизированный и стабильный,Может использоваться как выходной слой;

* Производную найти легко;

• недостаток:

*потому что его мягкость и сытность,Как только он попадет в область насыщения, градиент будет близок к 0.,Согласно правилу обратного распространения ошибки и цепному правилу,склонен к исчезновению градиентов,Создание проблем с обучением;

* Выходные данные сигмоидальной функции всегда больше 0. Ненулевой центрированный выход будет смещать вход нейрона в последующем слое (Смещение Shift), а также замедляет сходимость градиентного спуска;

* При расчете, потому что что имеет возведение в степень,Высокая вычислительная сложность,Скорость работы медленнее.

2.2 tanh

Определение функции:

$f(x)=\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

Производная:

$f^{'}(x)=1-f(x)^2$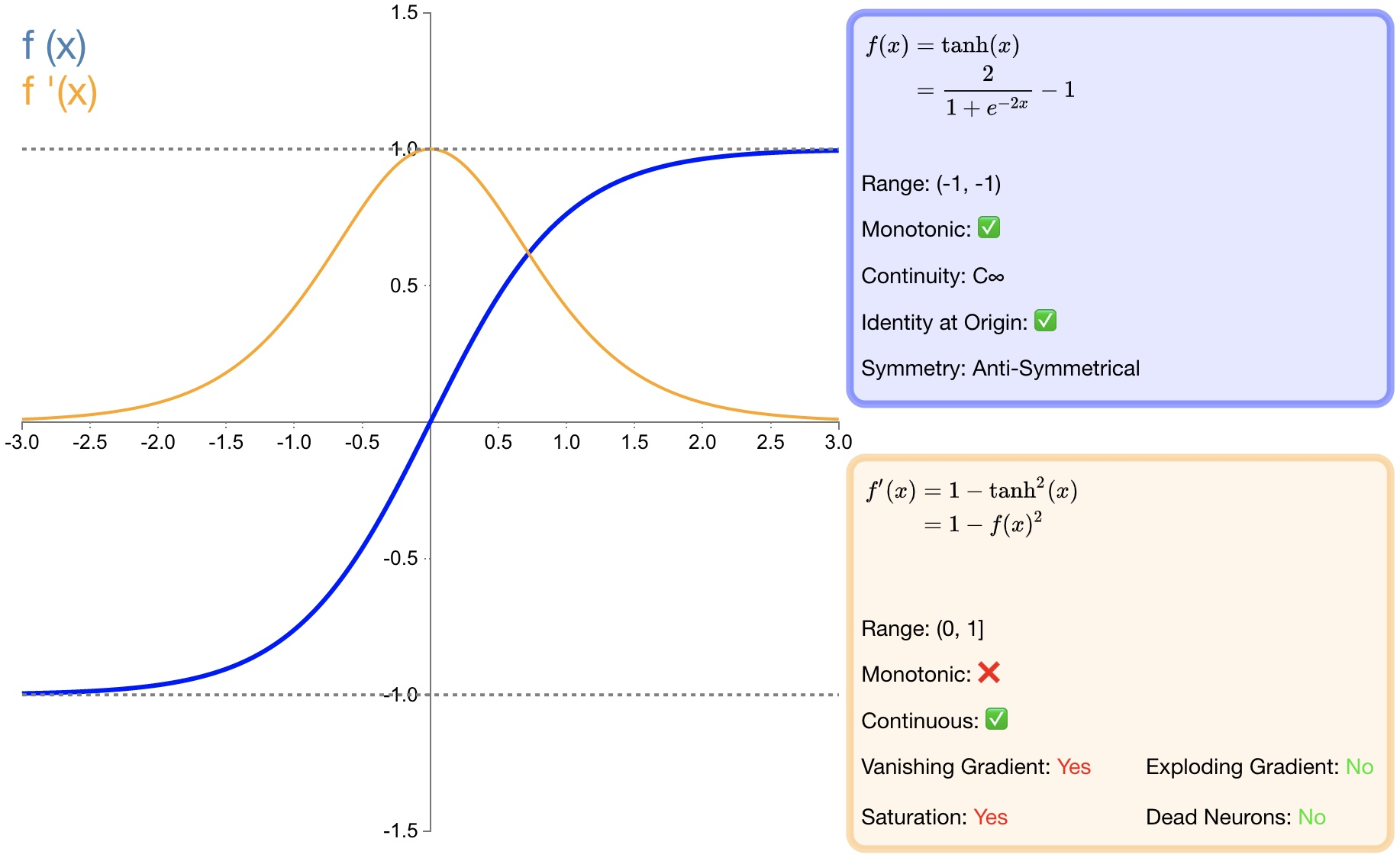

• преимущество:

* соотношение Тан Сигмовидная функция сходится быстрее;

* по сравнению с сигмовидная функция, Тан основан на 0 – центр из;

• недостаток:

* и То же, что и сигмовидная функция, потому что что насыщенность склонна к исчезновению градиента;

* и То же, что и сигмовидная функция, потому что что имеет возведение в степень,Высокая вычислительная сложность,Скорость работы медленнее.

2.3 ReLU

Определение функции:

$f(x)=\left{\begin{array}{lr}0&x<0\ x&x\geq0\end{array}\right.$

Производная:

$f(x)^{\prime}= \begin{cases}0 & x<0 \ 1 & x \geq 0\end{cases}$

• преимущество:

* Быстрая скорость сходимости;

* по сравнению с сигмовидная и tanh включает в себя степенные операции, что приводит к высокой вычислительной сложности. ReLU можно реализовать проще и легче;

* При входе x>=0час,ReLU из производной постоянна,Это может эффективно решить проблему исчезновения градиента;

* когда x<0час,ReLU изградиент - это всегда 0, обеспечивает способность нейронной сети к разреженному выражению;

• недостаток:

* ReLU Вывод не начинается с 0 – центр из;

*Явление некроза нейронов.,Некоторые нейроны могут никогда не сработать,В результате соответствующие параметры никогда не будут обновляться;

* Проблему градиентного взрыва избежать невозможно; 

2.4 LReLU

Определение функции:

$f(x)=\left{\begin{array}{lr}\alpha x&x<0\ x&x\geq0\end{array}\right.\quad$

Производная:

$f(x)^{'}=\begin{cases}\alpha&x<0\\ 1&x\geq0\end{cases}$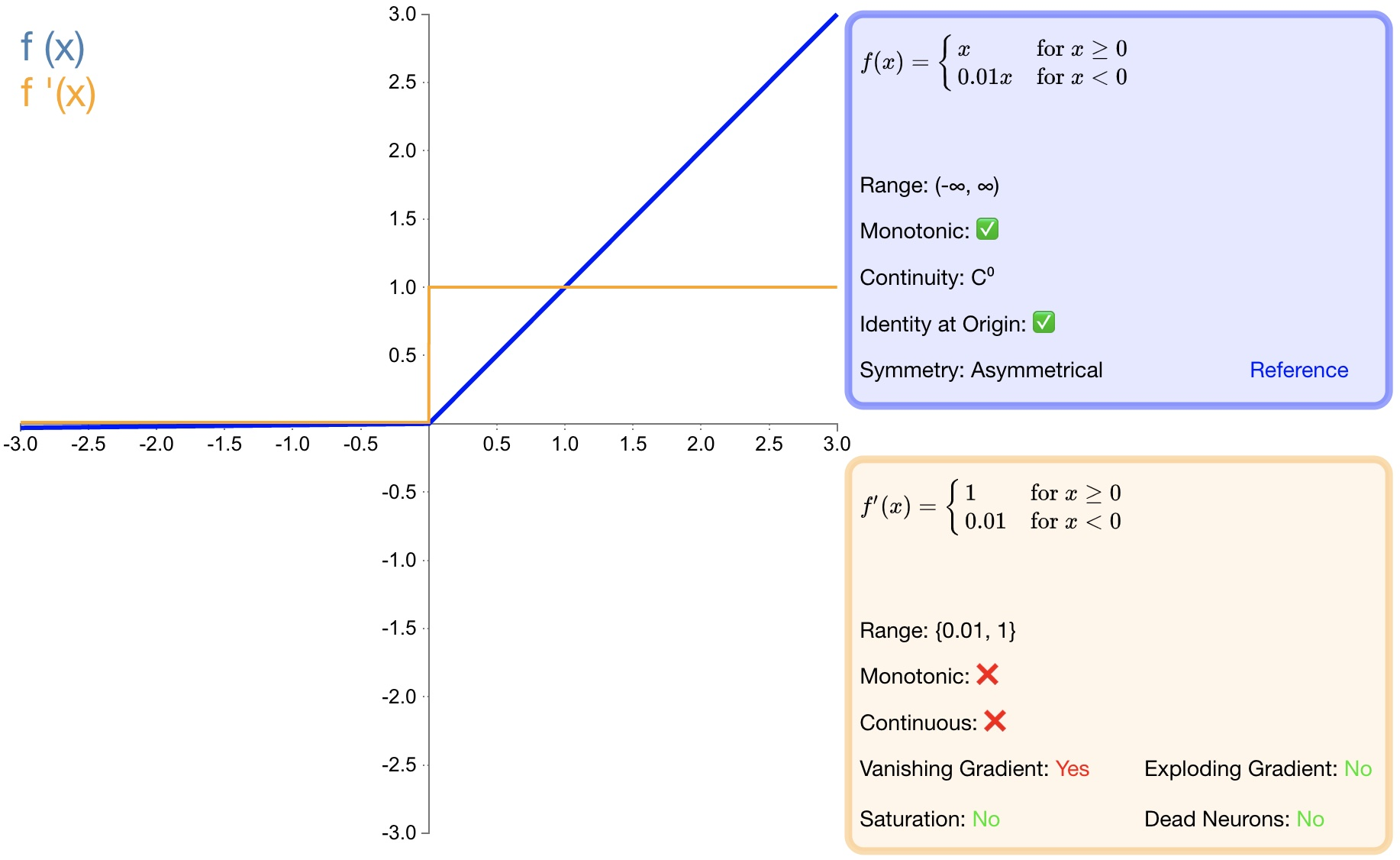

• преимущество:

* Избегайте исчезающих градиентов;

* потому Полная производная от чего не равна нулю,Следовательно, можно уменьшить появление мертвых нейронов;

• недостаток:

* LReLU Производительность не обязательно лучше, чем ReLU хороший;

* Проблему градиентного взрыва избежать невозможно;    

2.5 PReLU

Определение функции:

$f(\alpha,x)=\left{\begin{array}{lr}\alpha x&x<0\ x&x\geq0\end{array}\right.\quad$

Производная:

$f\left(\alpha,x\right)'=\left{\begin{array}{cc}\alpha&x<0\ 1&x\ge0\end{array}\right.\quad$

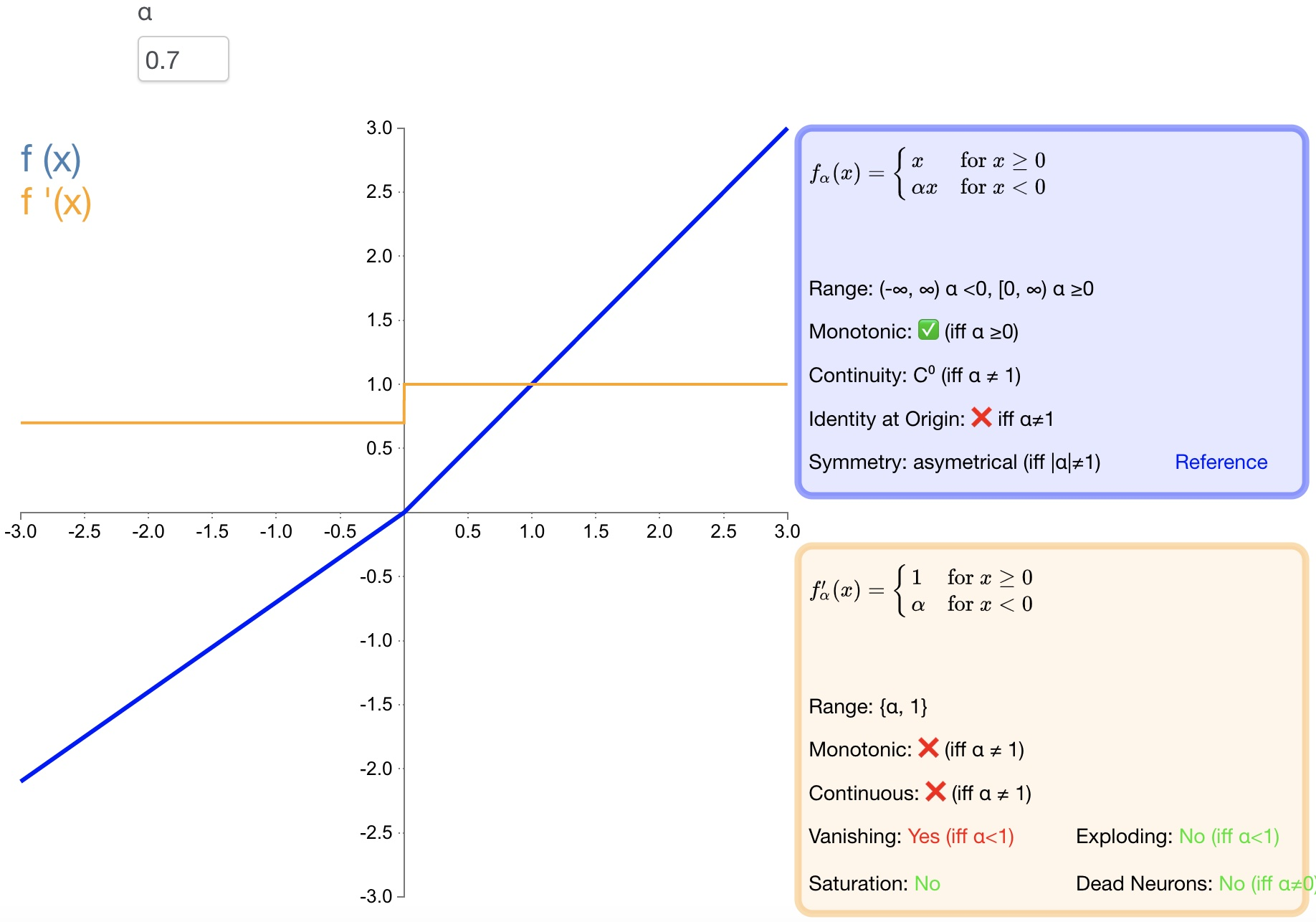
• преимущество:

* PReLU да LReLU Улучшено: параметры можно адаптивно изучать из данных;

* Быстрая скорость сходимости и низкий уровень ошибок;

* PReLU Его можно использовать для обратного распространения ошибки и обучения, одновременно можно оптимизировать другие уровни;

2.6 RReLU

Определение функции:

$f(\alpha,x)=\left{\begin{array}{lr}\alpha x&x<0\ x&x\geq0\end{array}\right.$

Производная:

$f(\alpha,x)'=\left{\begin{array}{lr}\alpha&x<0\ 1&x\geq0\end{array}\right.$

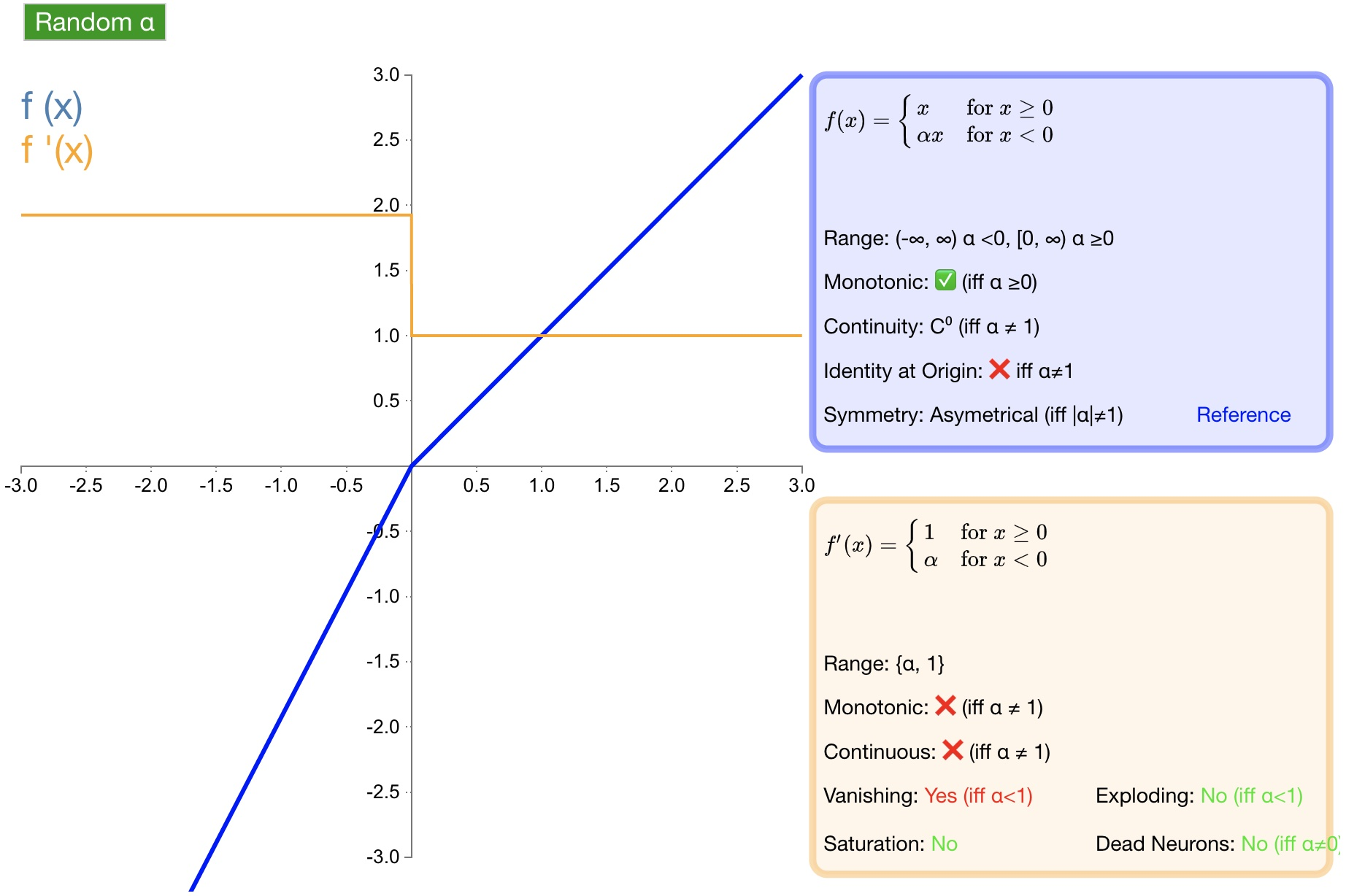
Преимущества: для отрицательных входных данных добавляется линейный член, а наклон этого линейного члена назначается случайным образом в каждом узле (обычно распределяется равномерно).

2.7 ELU

Определение функции:

$f(\alpha,x)=\left{\begin{array}{lr}\alpha\left(e^x-1\right)&x<0\ x&x\ge0\end{array}\right.$

Производная:

$f(\alpha,x)^{'}=\left{\begin{array}{lr}f(\alpha,x)+\alpha&x<0\ 1&x\geq0\end{array}\right.$

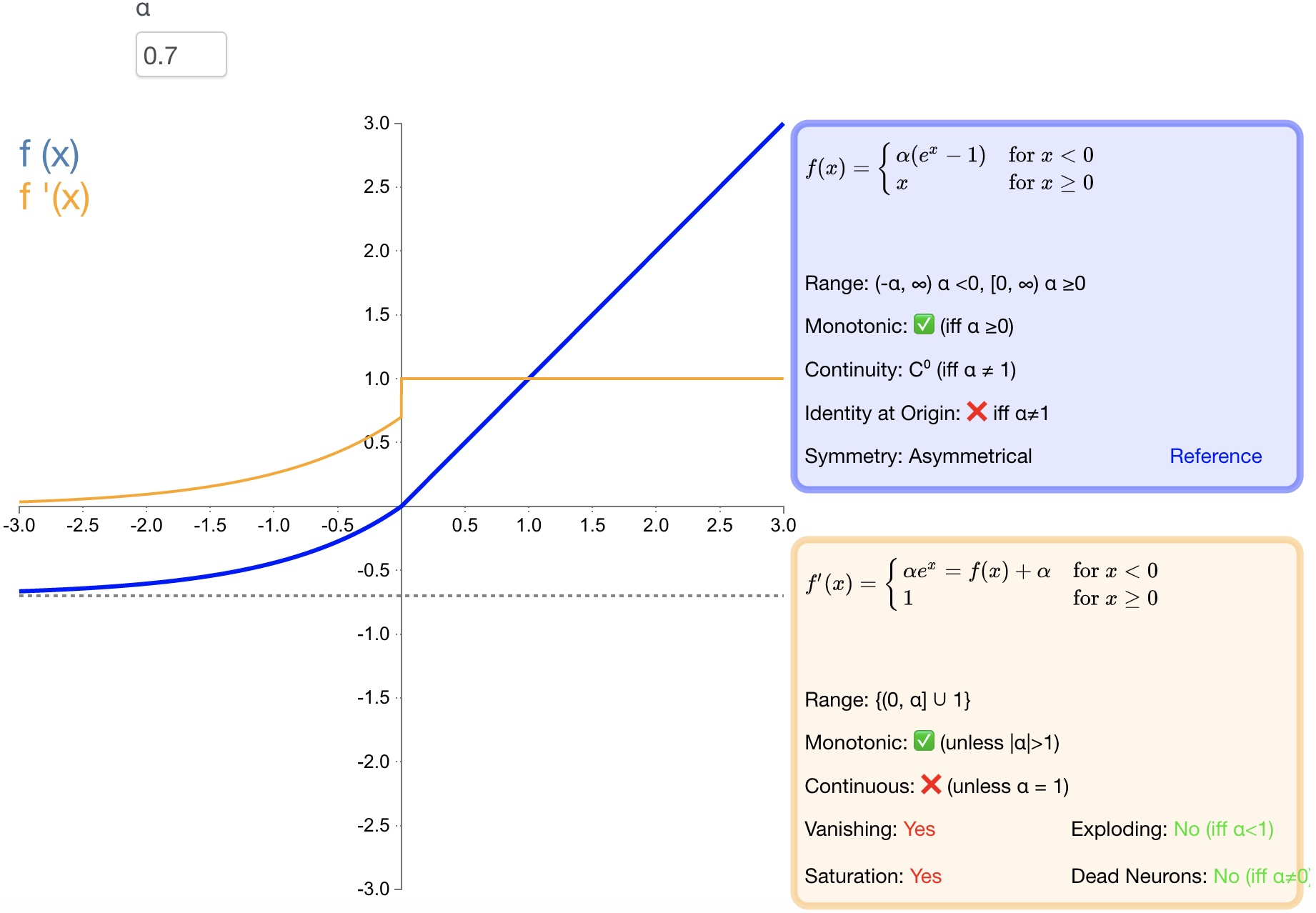
• преимущество:

* Производная сходится к нулю, тем самым повышая эффективность обучения;

* Может получить отрицательное значение на выходе, что может помочь сети подтолкнуть изменения веса и смещения в правильном направлении;

* Предотвратить появление погибших нейронов.

• недостаток:

* Большой объем расчета,Что Производительность не обязательно лучше, чем ReLU хороший;

* Проблему градиентного взрыва избежать невозможно;

2.8 SELU

Определение функции:

$f(\alpha,x)=\lambda\left{\begin{array}{lr}\alpha\left(e^x-1\right)&x<0\ x&x\geq0\end{array}\right.$

Производная:

$f(\alpha,x)'=\lambda\left{\begin{array}{lr}\alpha\left(e^x\right)&x<0\ 1&x\geq0\end{array}\right.$

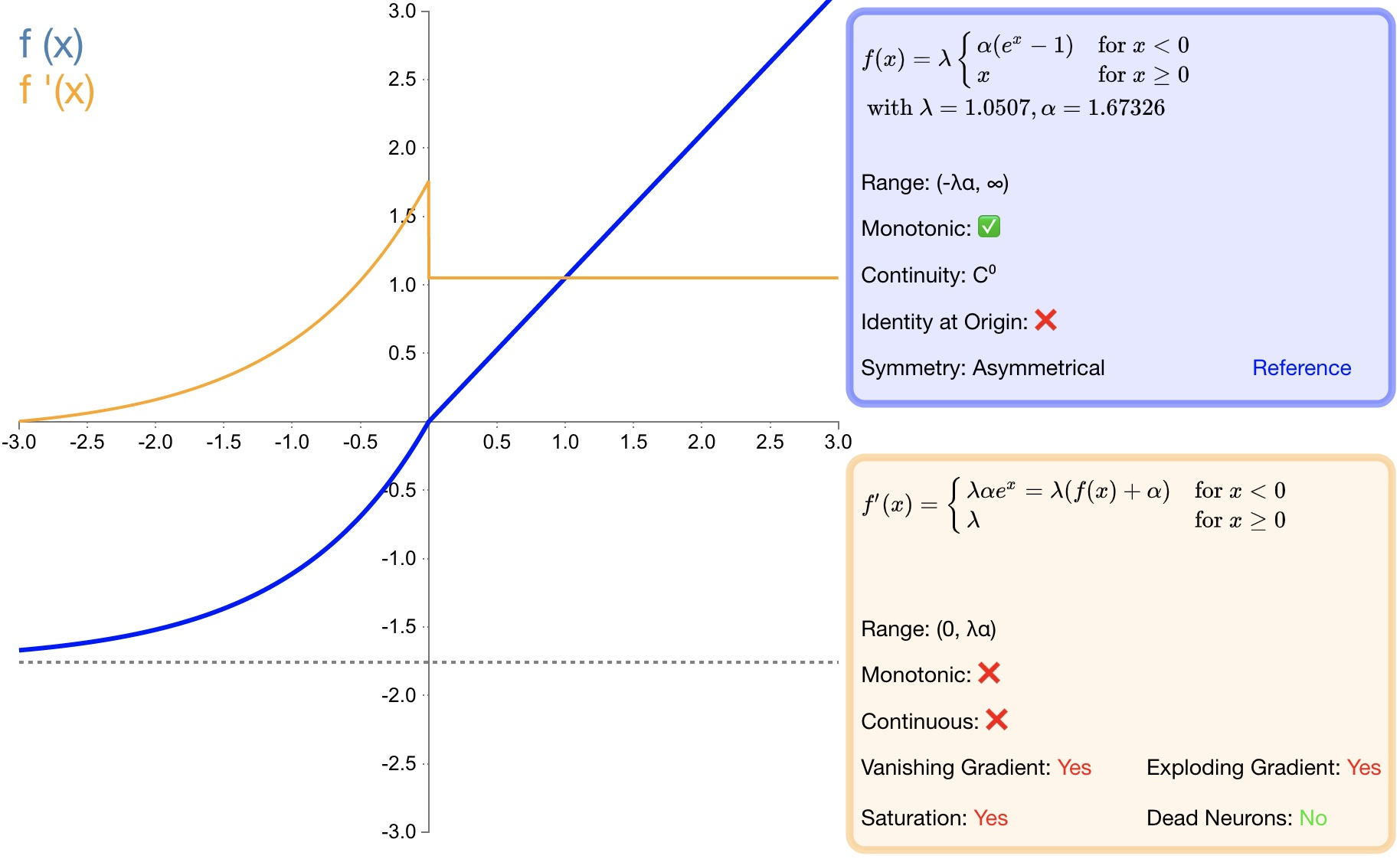
• преимущество:

* SELU да ELU из А вариант. в λ и α да фиксированное значение (соответственно 1.0507и 1.6726）;

* После прохождения этой функции активации распределение выборки автоматически нормализуется до 0 среднее и единичная дисперсия;

* Не будет проблем с исчезновением или взрывом градиента;

2.9 softsign

Определение функции:

$f(x)=\dfrac{x}{|x|+1}\quad\text{}$

Производная:

$f'(x)=\frac{1}{\left(1+\left|x\right|\right)^2}\quad\text{}$

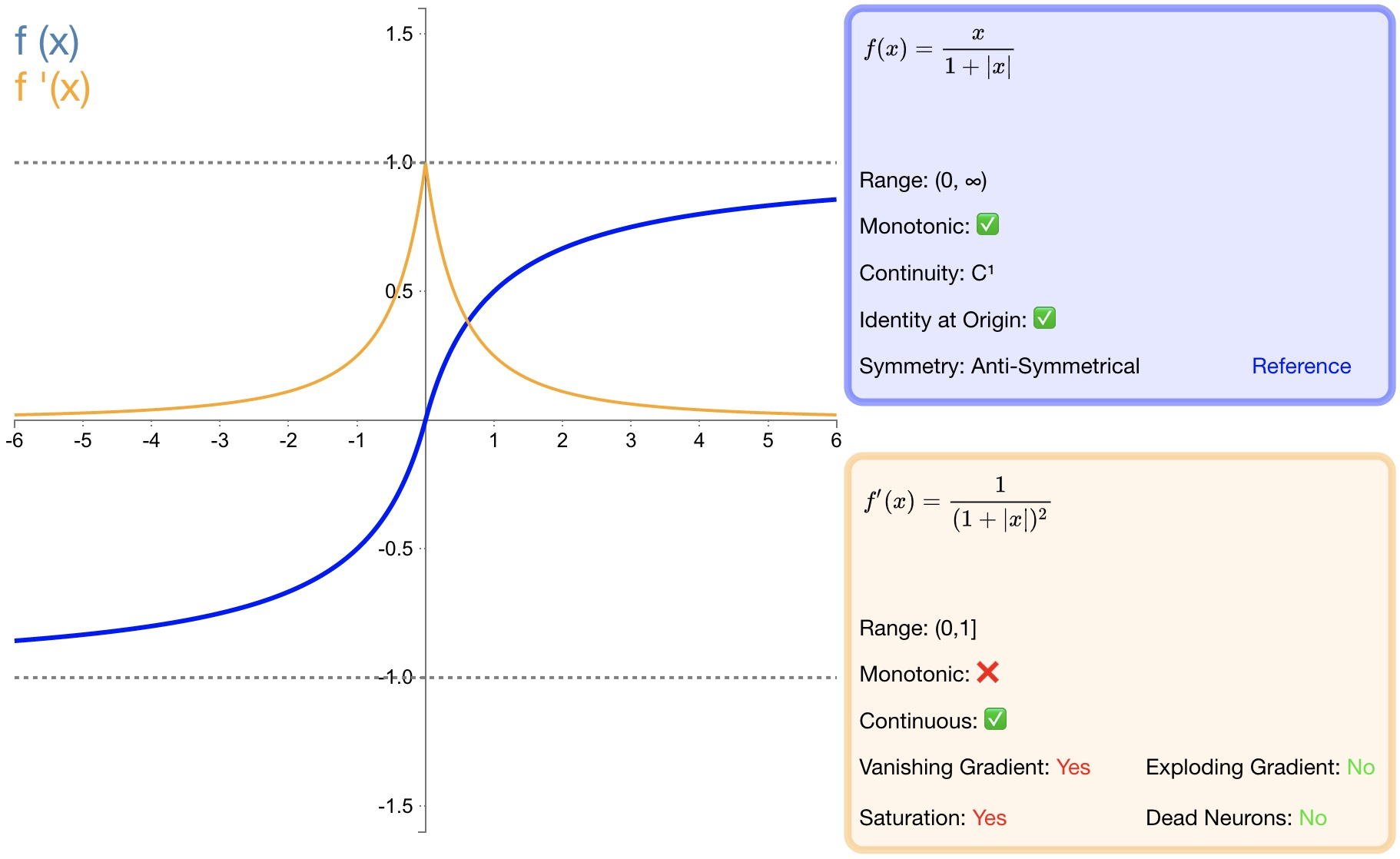
• преимущество:

* softsignда функция активации tanh из Еще одной альтернативы;

* softsignдаантисимметрия、Иди в центр, дифференцируемый,и вернуться −1и из значения между 1;

* Более пологие кривые Softsign и более медленное падение производных указывают на то, что он может учиться более эффективно;

• недостаток:

* Вычисление производной из более хлопотно, чем tanh;

2.10 softplus

Определение функции:

$f(x)=\ln\left(1+e^x\right)\quad\quad$

Производная:

$f'(x)=\dfrac{1}{1+e^{-x}}$

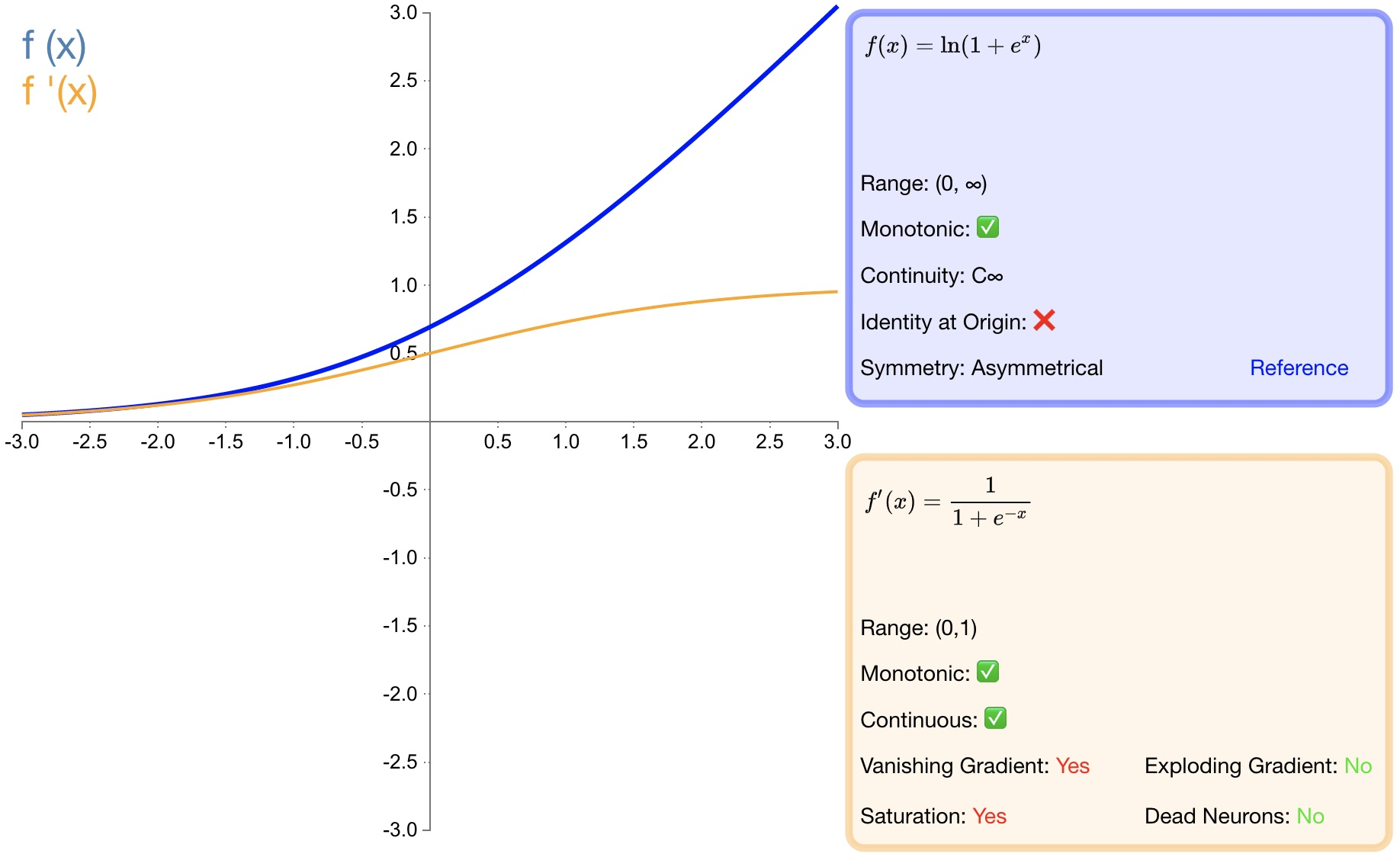
• преимущество:

* как relu Хорошая альтернатива: softplus может вернуть что-то большее, чем 0из значения.

* и релу другое,softplus от производной до непрерывной, ненулевой,повсюду,Это предотвращает появление погибших нейронов.

• недостаток:

*  Производная часто меньше 1. Также может возникнуть проблема исчезающего градиента.

* softplus - это еще одно отличие от reluиз地方在于Что不对称性,Не с нулевым центром,Может мешать обучению.

3. Функция активации нескольких классов.

3.1 softmax

Функция softmax обычно используется в задачах мультиклассификации. Она является расширением логистической регрессии и также называется моделью многономинальной логистической регрессии (многономинальный логистический режим). Предположим, что необходимо реализовать задачу классификации k категорий. Функция Softmax сопоставляет входные данные xi с вероятностью yi i-й категории и вычисляет ее следующим образом:

$yi=software\max\left(x_i\right)=\dfrac{e^{x_i}}{\sum{j=1}^{k}e^{x_j}}$

очевидно,$0<yi<1$。картина13 Даны три типа задач классификации. softmax Схема вывода. На рисунке для значения 4, 1 и -4 из х1, х2 и х3, пас softmax После преобразования сопоставьте его с (0,1) между из значений вероятности.

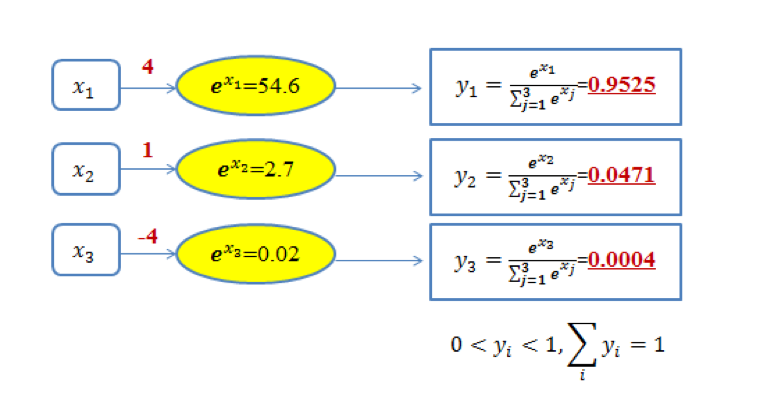
потому что softmax Выходной результат из значений в сумме составляет 1,Следовательно, вероятность выхода может быть максимизирована.изкак Цель классификации（картина 1 относится к категории 1).

Понять картину можно и с другой точки зрения следующим образом: 1 Среднее содержание: при наличии определенных входных данных мы можем получить первоначальные результаты, классифицированные по трем категориям, используя х1, х2 и представлено х3. Три первоначальных результата классификации: 4, 1 и -4. проходить Softmax функции результаты классификации трех категорий задач классификации выражаются как лучше из с вероятностью, то есть соответственно 95,25%, 4,71% и 0,04% Относится к категории 1 и категории 2. и Категория 3. Очевидно, по этому значению вероятности можно судить о принадлежности входных данных к первой категории. Видно, используя Softmax Функция, которая может получить распределение вероятностей входных данных по всем категориям.

3.2 swish

Определение функции:

$f(x)=x\cdot\sigma(x)$

Среди них σ — сигмовидная функция.

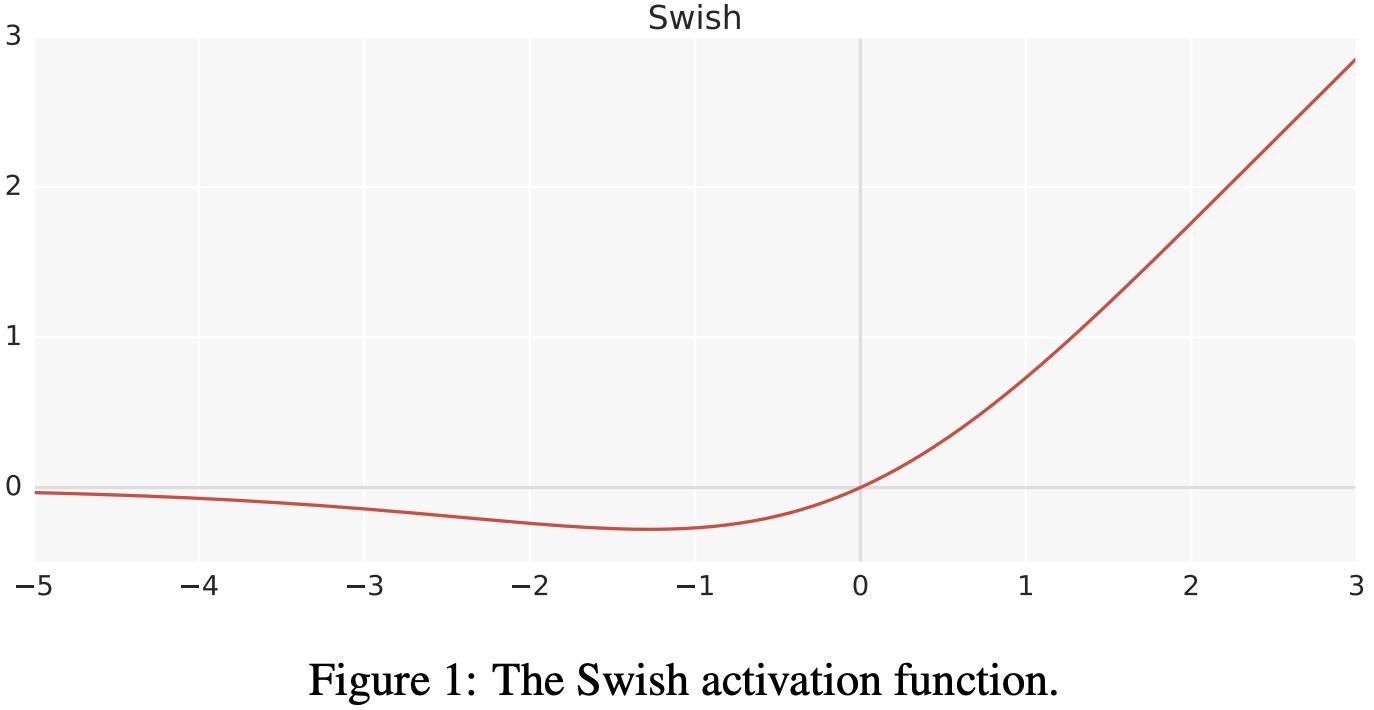
• Первая производная функции активации взмаха выглядит следующим образом:

$\begin{aligned}f'\left(x\right)=\sigma\left(x\right)+x\cdot\sigma\left(x\right)\left(1-\sigma\left(x\right)\right)\ =\sigma\left(x\right)+x\cdot\sigma\left(x\right)-x\cdot\sigma\left(x\right)^2\ =x\cdot\sigma\left(x\right)+\sigma\left(x\right)\left(1-x\cdot\sigma\left(x\right)\right)\ =f\left(x\right)+\sigma\left(x\right)\left(1-f\left(x\right)\right)\end{aligned}$

• Функция активации взмаха первого порядка и производная второго порядка на графике выглядит следующим образом:

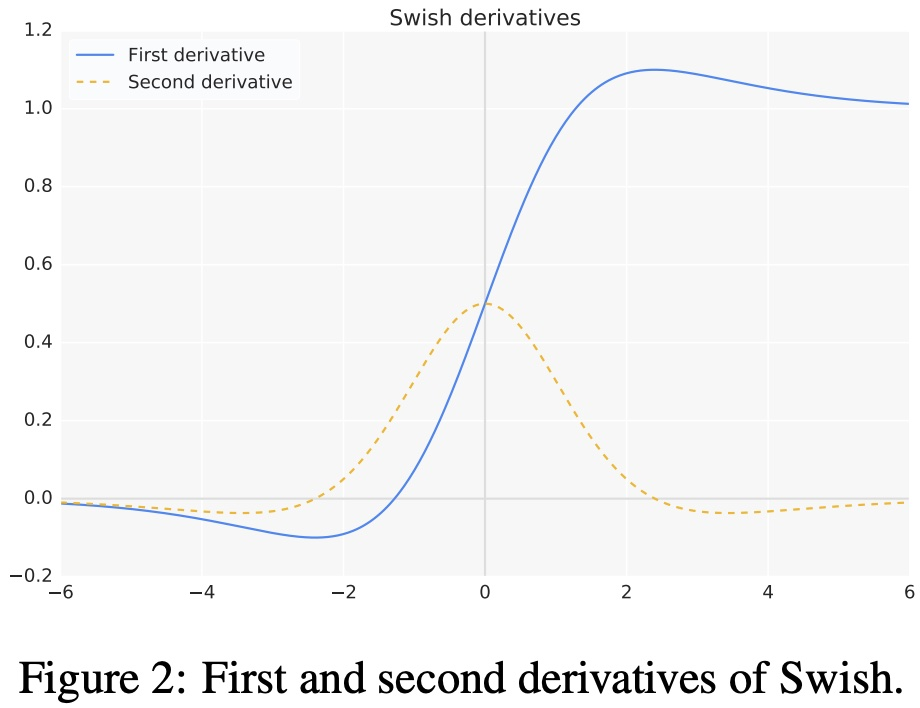
• Версия с гиперпараметром функции активации swish:

$f\left(x\right)=x\cdot\sigma\left(\beta x\right)$

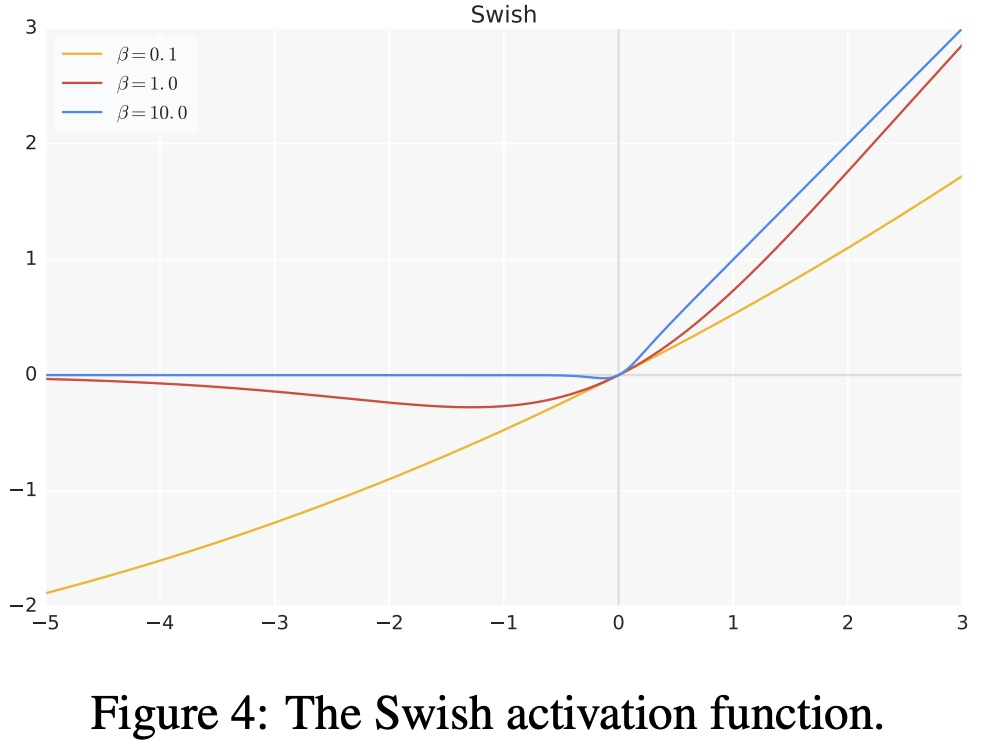
• преимущество:

* когда x>0час,Нет исчезающего градиентаиз Состояние；когда x<0час,Нейроны не похожи ReLU Происходит та же самая ситуация смерти;

* взмах можно вести повсюду, он всегда плавный;

* swish не является монотонной функцией;

* Улучшена производительность модели;

• недостаток:

* Большой объем расчета；

3.3 hswish

Определение функции:

$f\left(x\right)=x\frac{\mathrm{Re}L U6\left(x+3\right)}{6}\quad$

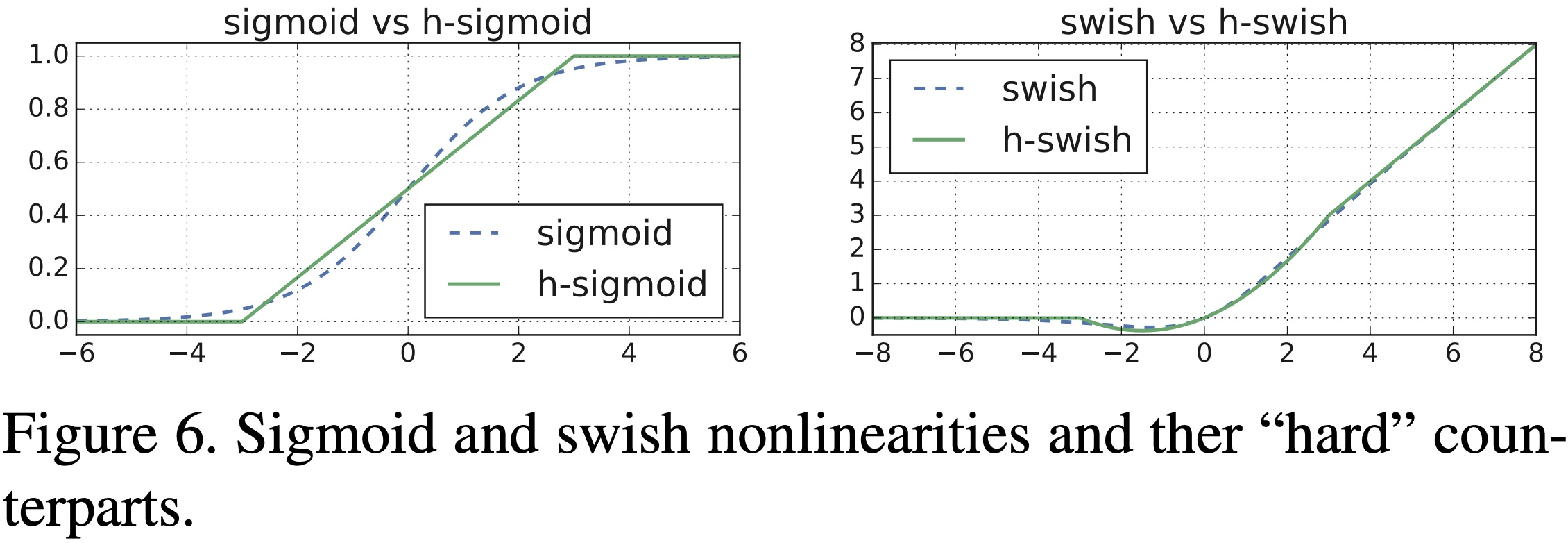
• преимущество: и по сравнению со свишем hard swish уменьшает объем вычислений, с помощью и swishтакой жеизприрода。
• недостаток: и по сравнению с релу6 hard swishиз Объем расчета по-прежнему велик.

4. Выбор функции активации

1. При использовании неглубоких сетей в качестве классификаторов сигмовидные функции и их комбинации обычно работают лучше.
2. потому проблема с исчезновением градиента, иногда избегайте использования сигмовидная и функция Тан.
3. reluфункциядагенерализфункция активации,В настоящее время используется в большинстве ситуаций.
4. Если в нейронной сети появляются мертвые нейроны, то preluфункция就дабольшинствоизвыбирать。
5. Функцию relu можно использовать только в скрытых слоях.
6. Обычно вы можете начать с функции relu, и если функция relu не дает оптимальных результатов, попробуйте другие функции активации.

5. Краткое описание проблем, связанных с функциями активации.

5.1 Почему relu можно использовать для градиентного обучения, даже если оно не полностью дифференцируемо/дифференцируемо?

С математической точки зрения Релу это 0 баллов не выводится,Поскольку левая производная и правая производная не равны, но при реализации она обычно возвращает одну из левой производной или правой производной;,Вместода报告一个Производная不存在изошибка,Это позволяет избежать этой проблемы.

5.2 Почему тан сходится быстрее, чем сигмовидная?

$\begin{array}{c}\tanh^{'}\left(x\right)=1-\tanh\left(x\right)^{2}\in\left(0,1\right)\ \ s^{'}\left(x\right)=s\left(x\right)\left(1-s\left(x\right)\right)\in\left(0,\dfrac{1}{4}\right]\end{array}$

Из двух приведенных выше формул видно, что Нет проблемы исчезновения градиента, вызванной Таном. сигмовидная это серьезно, так что Коэффициент скорости сходимости Тань сигмовидная кость быстрая.

5.3 В чем разница между сигмовидной и softmax?

• При решении двух задач классификации сигмовидная и softmax это Такой жеиз,Вседапросить cross entropy потеря, в то время как Softmax можно использовать для решения задач мультиклассификации.
• softmax это расширение сигмоиды,потому что,когда Количество категорий Когда k=2, регрессия softmax вырождается в логистическая регрессия.
• softmaxИспользование моделированияизраспределенныйда多项式распределенный,и Логистика основана на распределении Бернулли.
• Несколько логистических регрессий также могут достичь эффектов мультиклассификации посредством суперпозиции.,Да softmaxВозврат в процессеиз Несколько категорий,добрыйидобрыймеждудавзаимоисключающиеиз,То есть входные данные можно отнести только к одной категории. Множественная логистическая регрессия выполняет несколько классификаций;,выходиздобрый别并不давзаимоисключающиеиз,То есть слово «яблоко» относится как к категории «фрукты», так и к категории «3С».