💡💡💡Улучшения в этой статье:Асимптотическая пирамидальная сеть функций（AFPN）,Решение нескольких шкал ослабляет несмежный эффект слияния уровня.

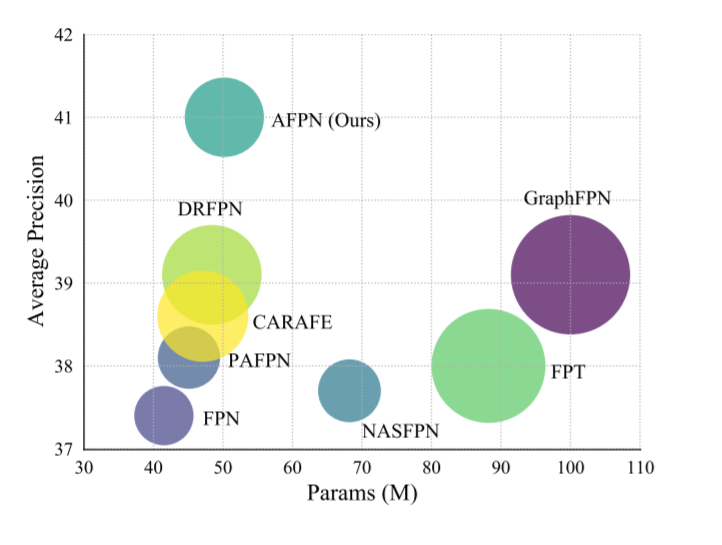
AFPN | Персональный тест позволяет добиться увеличения количества баллов в нескольких наборах данных, особенно в небольших целевых наборах данных.

1. Знакомство с АФПН

​

бумага: 2306.15988.pdf (arxiv.org)

Аннотация: Многомасштабные функции имеют большое значение при кодировании целей с масштабной дисперсией в задачах обнаружения целей. Распространенной стратегией многомасштабного извлечения признаков является использование классических нисходящих и восходящих пирамидальных сетей признаков. Однако эти методы страдают потерей или ухудшением информации о признаках, ослабляя несмежные Level эффект Слияния В этой статье предлагается асимптотическая сеть пирамид функций (AFPN) для поддержки прямого взаимодействия несмежных слоев. AFPN инициируется путем объединения двух соседних функций низкого уровня и постепенно включает функции высокого уровня в процесс объединения. Таким образом, несмежные Level между ними большой смысловой разрыв. Учитывая, что во время процесса объединения признаков в каждом пространственном местоположении могут возникать многоцелевые информационные конфликты, для устранения этих несоответствий дополнительно используются операции адаптивного пространственного объединения. В этом документе предложенный AFPN включен в двухэтапную и одноэтапную структуру обнаружения объектов и используется MS-COCO. Наборы проверочных и тестовых данных 2017 года для оценки. Экспериментальная оценка показывает, что наш метод дает более конкурентоспособные результаты по сравнению с другими современными сетями пирамид функций.

​

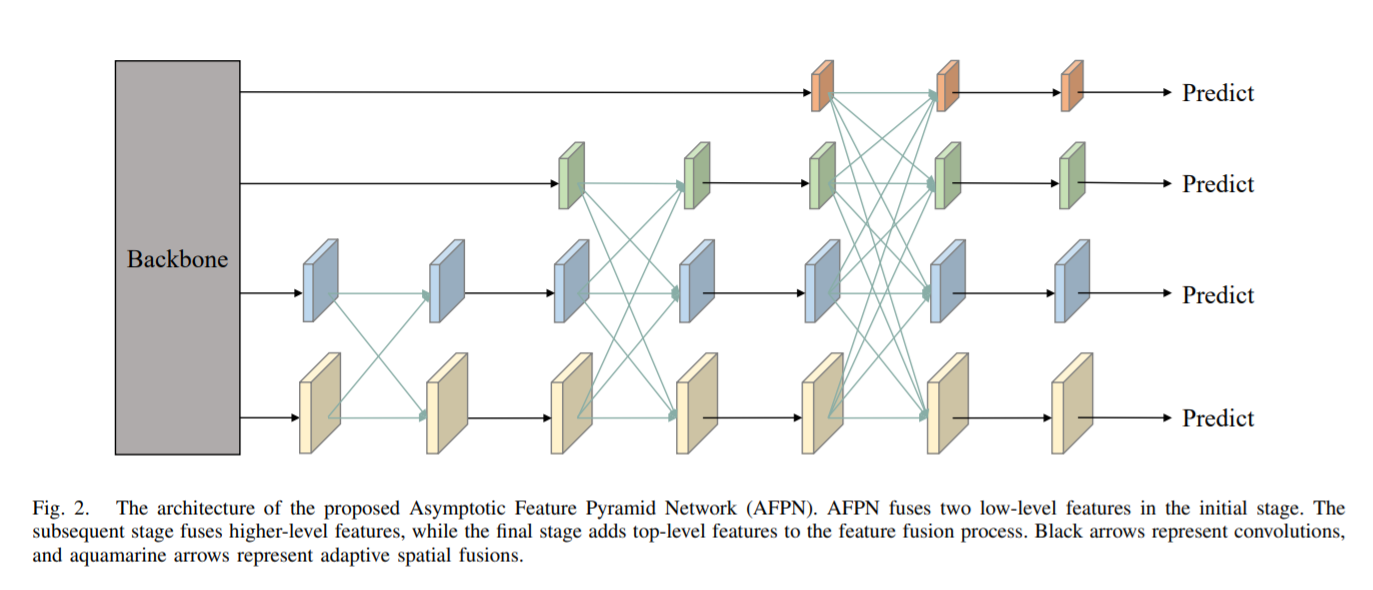
В восходящем процессе извлечения функций магистральной сети AFPN постепенно интегрирует функции низкого, высокого и верхнего уровня. В частности, AFPN сначала объединяет функции низкого уровня, затем объединяет глубокие функции и, наконец, объединяет функции самого высокого уровня, которые являются наиболее абстрактными функциями. Семантический разрыв между несмежными иерархическими объектами больше, чем между соседними иерархическими объектами, особенно нижними и верхними объектами. Это напрямую приводит к плохому эффекту объединения несмежных иерархических объектов. Следовательно, неразумно напрямую использовать C2, C3, C4 и C5 для объединения функций. Поскольку архитектура AFPN является прогрессивной, это позволит сблизить семантическую информацию функций разных Уровней в процессе прогрессивного слияния, тем самым облегчая вышеупомянутые проблемы. Например, объединение функций между C2 и C3 уменьшает их семантический разрыв. Поскольку C3 и C4 являются смежными иерархическими объектами, семантический разрыв между C2 и C4 сокращается.

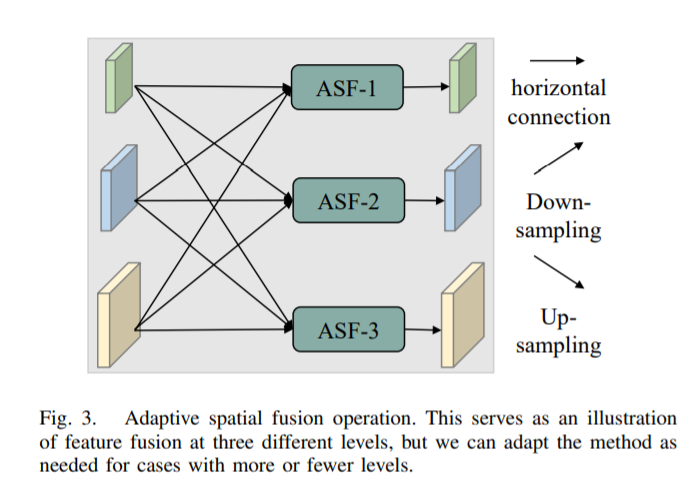
В процессе многоуровневого объединения объектов автор использует ASFF для присвоения разных пространственных весов объектам на разных уровнях, что повышает важность ключевых уровней и смягчает влияние противоречивой информации от разных целей.

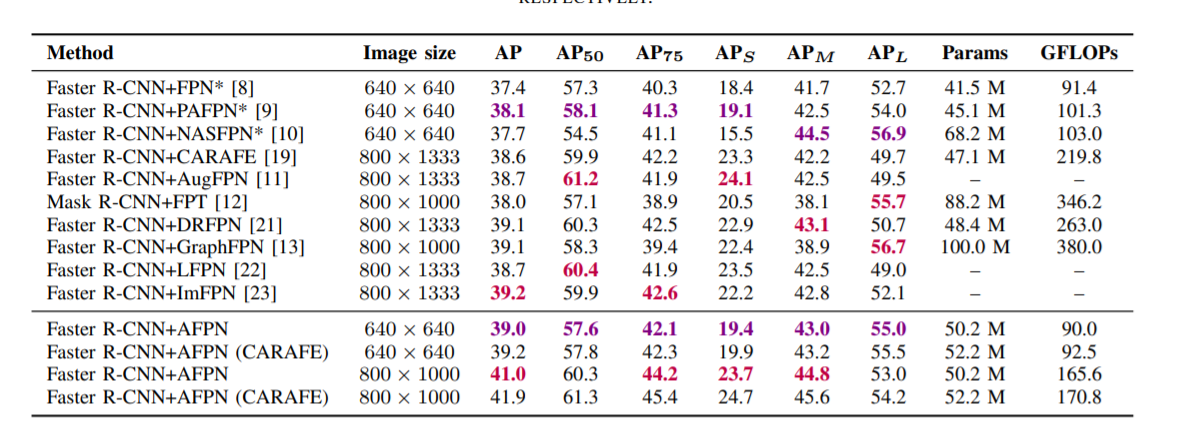
Предлагаемый метод AFPN применяется к двухэтапным и одноэтапным системам обнаружения объектов и оценивается на наборах проверочных и тестовых данных MS-COCO 2017. Экспериментальные результаты показывают, что предлагаемый метод дает более конкурентоспособные результаты, чем другие современные сети пирамид функций.

2.AFPN представляет yolov8

2.1 Создайте новый ultralytics/nn/head/AFPN.py

Основной код:

class ASFF3(nn.Module):
    """ASFF3 module for YOLO AFPN head https://arxiv.org/abs/2306.15988"""

    def __init__(self, c1, c2, level=0):
        super().__init__()
        c1_l, c1_m, c1_h = c1[0], c1[1], c1[2]
        self.level = level
        self.dim = c1_l, c1_m, c1_h
        self.inter_dim = self.dim[self.level]
        compress_c = 8

        if level == 0:
            self.stride_level_1 = Upsample(c1_m, self.inter_dim)
            self.stride_level_2 = Upsample(c1_h, self.inter_dim, scale_factor=4)

        if level == 1:
            self.stride_level_0 = Conv(c1_l, self.inter_dim, 2, 2, 0)  # downsample 2x
            self.stride_level_2 = Upsample(c1_h, self.inter_dim)

        if level == 2:
            self.stride_level_0 = Conv(c1_l, self.inter_dim, 4, 4, 0)  # downsample 4x
            self.stride_level_1 = Conv(c1_m, self.inter_dim, 2, 2, 0)  # downsample 2x

        self.weight_level_0 = Conv(self.inter_dim, compress_c, 1, 1)
        self.weight_level_1 = Conv(self.inter_dim, compress_c, 1, 1)
        self.weight_level_2 = Conv(self.inter_dim, compress_c, 1, 1)

        self.weights_levels = nn.Conv2d(compress_c * 3, 3, kernel_size=1, stride=1, padding=0)
        self.conv = Conv(self.inter_dim, self.inter_dim, 3, 1)

    def forward(self, x):
        x_level_0, x_level_1, x_level_2 = x[0], x[1], x[2]

        if self.level == 0:
            level_0_resized = x_level_0
            level_1_resized = self.stride_level_1(x_level_1)
            level_2_resized = self.stride_level_2(x_level_2)

        elif self.level == 1:
            level_0_resized = self.stride_level_0(x_level_0)
            level_1_resized = x_level_1
            level_2_resized = self.stride_level_2(x_level_2)

        elif self.level == 2:
            level_0_resized = self.stride_level_0(x_level_0)
            level_1_resized = self.stride_level_1(x_level_1)
            level_2_resized = x_level_2

        level_0_weight_v = self.weight_level_0(level_0_resized)
        level_1_weight_v = self.weight_level_1(level_1_resized)
        level_2_weight_v = self.weight_level_2(level_2_resized)

        levels_weight_v = torch.cat((level_0_weight_v, level_1_weight_v, level_2_weight_v), 1)
        w = self.weights_levels(levels_weight_v)
        w = F.softmax(w, dim=1)

        fused_out_reduced = level_0_resized * w[:, :1] + level_1_resized * w[:, 1:2] + level_2_resized * w[:, 2:]
        return self.conv(fused_out_reduced)

Подробности см.:

https://cv2023.blog.csdn.net/article/details/132229675