Поскольку я скопировал это здесь, если есть какие-либо проблемы с форматированием, я рекомендую вам перейти прямо на мой исходный веб-сайт и проверить это: Модель камеры и преобразование координат - Теория большого взрыва

Оглавление

• Система координат долготы и широты относительно прямоугольной системы координат Земли.
• Геодезическая декартова система координат в систему координат долготы и широты
• географическая система координат изменять Геодезические координаты
• От системы координат тела к географической системе координат
• Система координат камеры относительно системы координат тела
• От системы координат изображения к системе координат пикселя
• От системы координат камеры к системе координат изображения
• От мировой системы координат к системе координат камеры
• Мировая система координат в пиксельную систему координат
• Преобразование координат при преобразовании перспективы
• система координат
  • Универсальный поперечный Меркатор UTM
• Формула преобразования координат
  • WGS84 <–> UTM
• Программное обеспечение для преобразования координат
• Программное обеспечение для 3D-рисования
• тестовый код
• Информационная рекомендация
• отступление

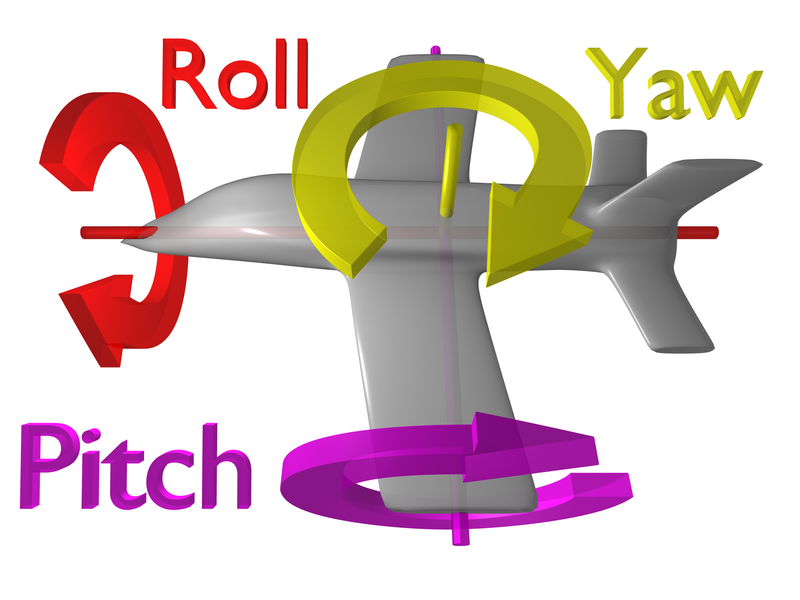
7 систем координат:

• Система координат тела：единицаm,Это прямоугольная система координат, в которой в качестве начала координат используется положение самолета.,Ось X указывает направление головки машины.,Ось Z направлена ​​вертикально вниз от самолета-носителя. То есть с отношением.
• географическая система координат：единицаm,Северо-восточная система координат NED установлена ​​с использованием положения самолета-носителя в качестве исходной точки.
• Геодезическая декартова система координат：единицаm,Декартова прямоугольная система координат, установленная на основе опорного эллипсоида.,Начало координат — это центральная точка опорного эллипсоида.,ZОсь указывает от начала координат до Северного полюса Земли.; Ось X указывает от начала координат до точки пересечения окружности нулевого меридиана и экваториальной окружности на эллипсоиде;
• Система координат WGS84：иГеодезическая декартова система координатТакой же,просто принятьШирота (М)、Долгота (L)иВысота земли (H)Представляет любую позицию точки в пространстве。
• Пиксельная система координат：единицаpixel,плоскость изображения камеры,Начало координат находится в изображенииверхний левый,ось U вправо,ось v вниз,Пиксельная система координат的единица是Пиксель(pixel),То естьразрешение。
• Система координат изображения：единицаmm,и Пиксельная система координата находится в одной плоскости. Начало координат — это пересечение оптической оси камеры и плоскости изображения. Обычно это середина плоскости изображения или главная точка. точка. Единицы измерения – это физические единицы.
• система координат камеры：единицаm,Начало координат – оптический центр,xиy轴и Пиксельная система Ось координат параллельна оси v, а ось z является оптической осью камеры. Расстояние от оптического центра до плоскости Пикселя — фокусное расстояние f. система координат камеры上的点и成像平面坐标系上的点存在перспективная проекциясвязь。

От системы координат широты и долготы БПЛА к геодезической прямоугольной системе координат:

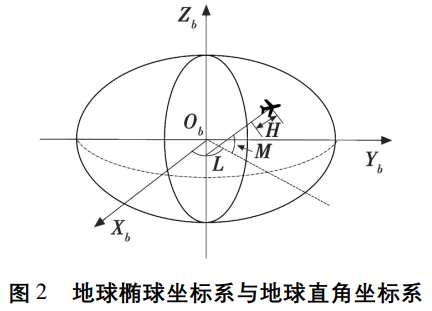
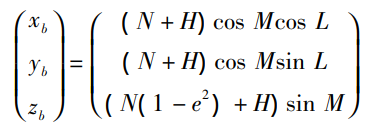
e представляет собой первый эксцентриситет земного эллипсоида; N представляет собой местоположение дрона; Радиус кривизны круга Маою в данной позиции. Соответственно выражается как:

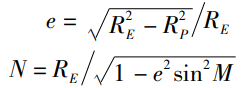
большая полуось RE = 6378137 м, малая полуось RP = 6356752 м

Геодезическая декартова система координат в систему координат долготы и широты

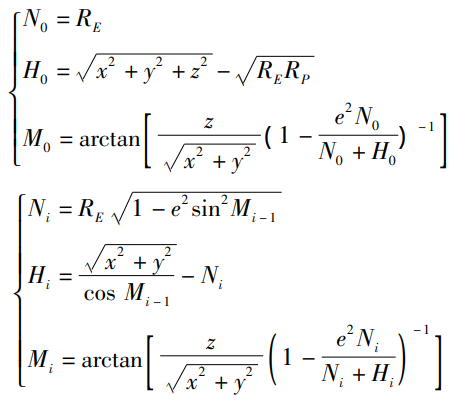
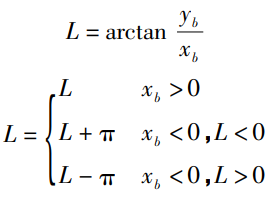
Уточнено, что широта северного полушария положительна, а широта южного полушария отрицательна; Восточная долгота положительна, а западная долгота отрицательна. Итерировать 4 ～ 5 Это может гарантировать, что точность расчета высоты целевой площадки достигнет 0.001 м, точность расчета широты цели достигает 0.00001°。

Географическая система координат в геодезическую систему координат

Матрица перевода вращения:

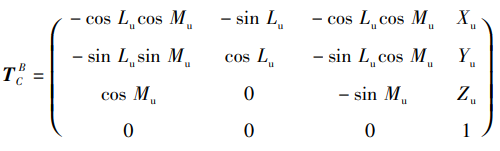
От системы координат тела к географической системе координат

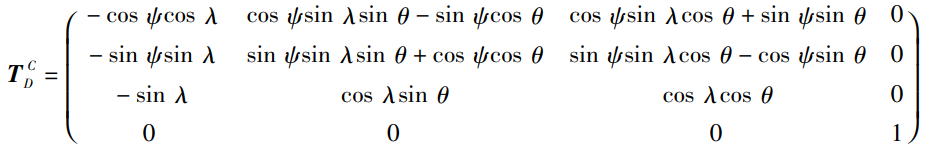
Я вышел из приведенной выше формулы и обнаружил, что, похоже, возникла проблема. Вы можете подтвердить еще раз:

-cos(yaw)*cos(pitch) должно быть cos(yaw)*cos(pitch) sin(yaw)*sin(pitch) должно быть sin(yaw)*cos(pitch)

Курс ψ: с севера на восток положительный. Шаг λ: направление вверх положительное. Крен θ: Наклон вправо положителен.

Последовательность эталонного преобразования:

Дальнейшее объяснение:

Выбор матрицы:

Для правосторонней системы определенное вращение вперед — это направление против часовой стрелки вокруг оси вращения, поэтому, когда объект действия (или объект вращения) является точкой или вектором в системе координат, следует использовать формулу (2), но когда Если объектом вращения является сама система координат (системой координат должна быть опорная система координат), то следует использовать формулу (1), наоборот, в левой системе определяется положительное направление по часовой стрелке, тогда; следует использовать противоположную формулу. 【Мы здесь => Правая система координат + сама вращающаяся система координат]

• Вращатьсяизменятьзаказ：внешнее вращение(z->y->x)、пронация(x->y->z)
• В соответствии с каждым изменением вращения изменяется вращение оси после изменения вращения.,Или фиксированная ось вращения,Разложим углы Эйлера напронация（intrisic roatation）ивнешнее вращение(extrinsic rotation)
• Rснаружи=R(Z)R(Y)R(X)
• В пределах R=R(a)R(b)R(c)

• Трансформация позы относительно тела Модели.,это пронация,Это вне всякого сомнения,То есть рыскание-Подача-роллизменить.
• На что нам нужно обратить внимание, так это,Умножение матриц — это внешнее вращение. Когда мы меняем отношение Модели через матрицу,Правильная операция — сначала накатить изменения.,Снова Подача,Наконец-то рысканье.
• Но почему правильно выйти первым?,Насколько я понимаю, это,Вращение изменения должно, прежде всего, вращением вокруг оси головки машины, чтобы иметь практическое значение.,Если мы сначала отклонимся на 45 градусов вокруг y,Тогда обходите z или xПодача,Наконец я обнаружил, что последняя ось была неправильной.
• (Исходное сообщение выше было 404... больше не буду его публиковать)
• 绕大地坐标系Вращатьсяизменять(оно не движется)это матрица в последовательностиЕхать направо,Это Зикс.
• 绕载体坐标系Вращатьсяизменять(оно не движется)это матрица в последовательностиПоверните налево,Это XYZ.
• Отношения обмена между модифицируемым внутренним спином и изменяемым внешним спином: поменяйте местами позиции первого и третьего модифицируемых спинов, и результаты будут одинаковыми.
• Правосторонняя система работает против часовой стрелки, а левая система — по часовой стрелке.

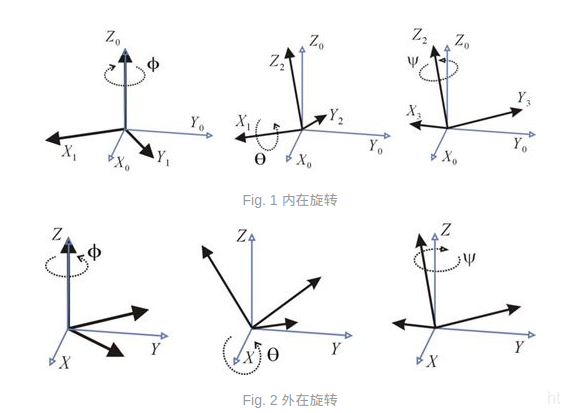
Система координат камеры относительно системы координат тела

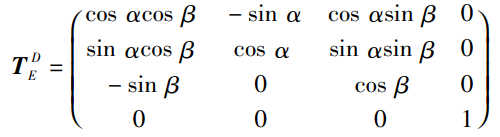
α и β — соответственно угол азимута и угол возвышения, когда фотоэлектрическая платформа собирает изображения; Обратите внимание, что приведенная выше формула представляет собой вращение по умолчанию (-α, -β), поэтому обратите внимание на знак. . .

От системы координат изображения к системе координат пикселя

Пиксель и изображения

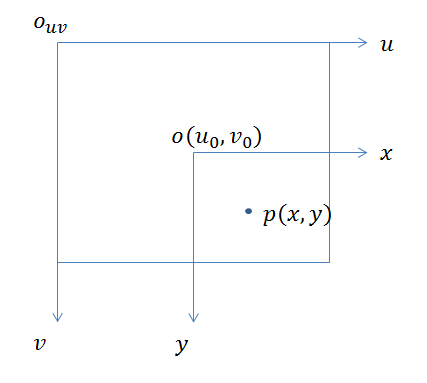
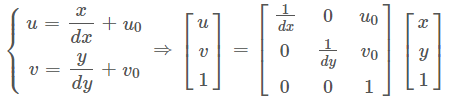
Координаты плоскости изображения, соответствующие p, представляют собой (x, y), а dx и dy представляют физический размер каждого пикселя изображения в плоскости изображения. Координаты начала плоскости изображения в системе координат пикселя: (u0, v0).

От системы координат камеры к системе координат изображения

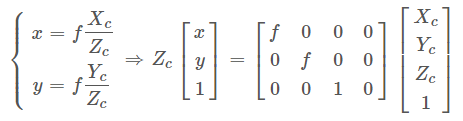
См. расчет Zc: Zc — проекция цели на ось Z системы координат камеры.

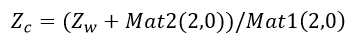
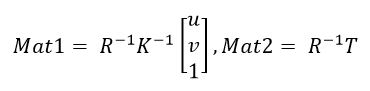
От мировой системы координат к системе координат камеры

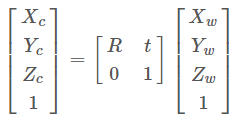
Мировая система координат в пиксельную систему координат

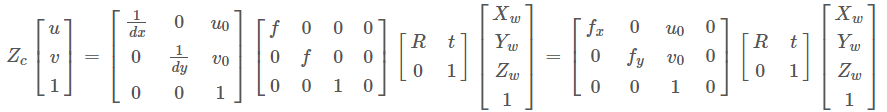
Внутренняя матрица параметров K представляет собой фиксированное значение и определяется после калибровки камеры, матрица внешних параметров T различна для каждого изображения и ее необходимо предоставить. Из соотношения преобразования между мировой системой координат и системой координат пикселей можно узнать, что координаты пикселей могут быть получены, если известны координаты трехмерной точки в мировой системе координат и матрицы внутренних и внешних параметров известно. И если известны координаты пикселей, даже если известны внутренние и внешние матрицы параметров, трехмерная точка по мировым координатам определяется не однозначно, а прямая линия в пространстве. То есть монокулярная камера может измерять только информацию о плоскости, но не может получать информацию о глубине.

Преобразование координат при преобразовании перспективы

Все вышеперечисленноеТрансформация твердого тела,Но когда настоящая камера наклонена,будет существоватьперспективная трансформация。

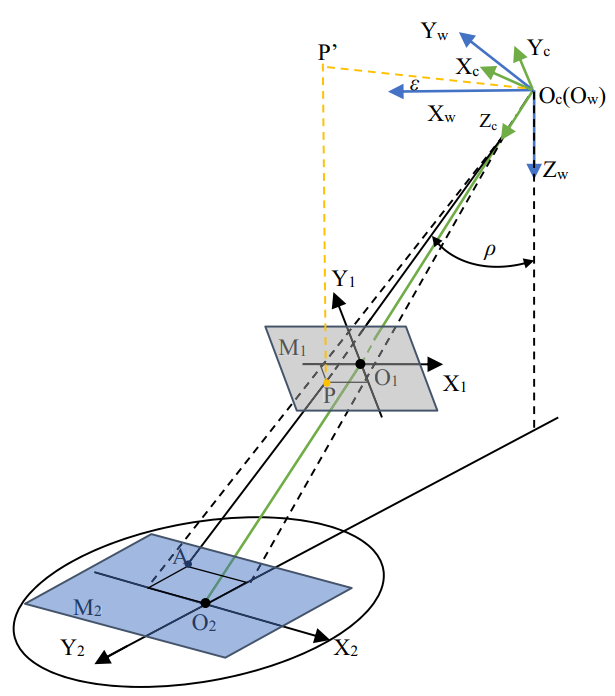
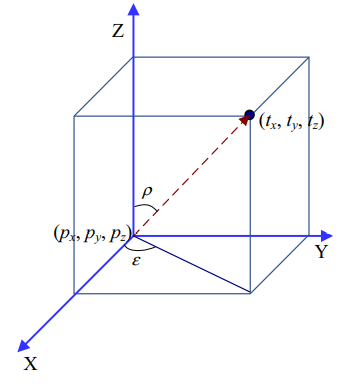
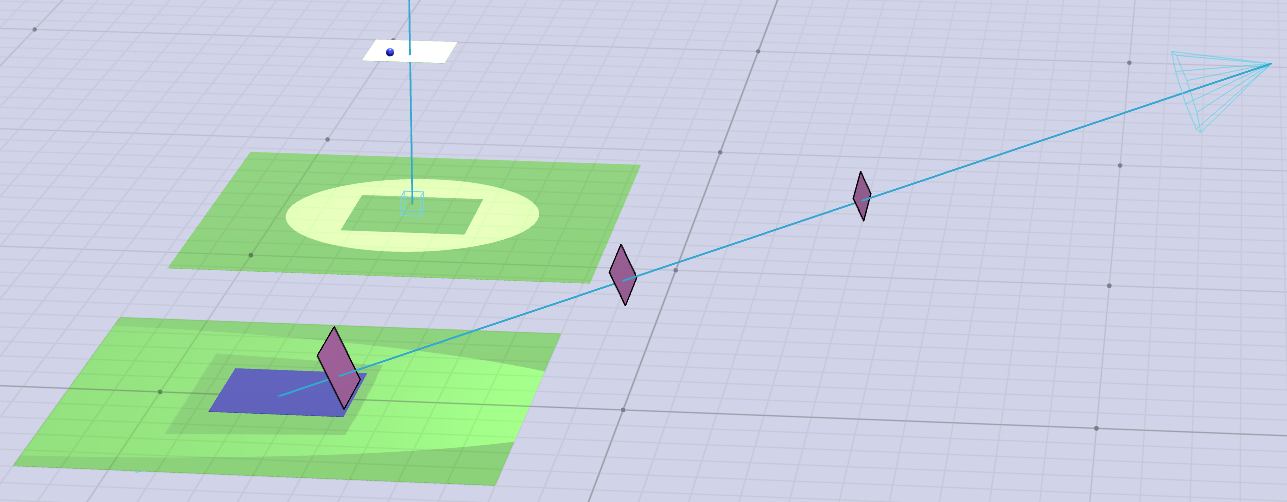
Следующий контент взят из " Ссылка 1”：   В процессе позиционирования цели БПЛА модуль слежения EOSTP регулирует углы азимута и возвышения камеры с помощью сервопривода, чтобы гарантировать, что целевая точка попадает в поле зрения камеры. недалеко от центра。 Таким образом, визуальное расстояние камеры может эффективно отражать позиционное соотношение между целевой точкой и дроном.   Угол ЛОС ($\rho,\epsilon$) определяется, как показано на рисунке 4. $\rho$ — угол между вектором ЛОС и осью z мировой системы координат, $\epsilon$ — угол между вектором LOS на плоскости $X_wO_wY_w$ Угол между проекцией и осью x мировой системы координат. $q$ и $\epsilon$ определяются положением дрона, углом азимута и углом возвышения камеры.   На рисунке 4 $M_1$ и $M_2$ представляют плоскость изображения и плоскость объекта соответственно. В M1 O — точка пересечения плоскости изображения и оптической оси камеры, а $O_1X_1$ и $O_1Y_1$ — две оси в горизонтальном и вертикальном направлениях плоскости изображения. P — точка проекции целевой точки A на плоскость изображения, а ее физические координаты изображения — $(x_p, y_p)$。$P ^ { \prime }$ — проекция P на плоскость $O_w-X_wY_w$. В M2 $O_2$ — это точка пересечения оптической оси камеры и плоскости объекта. $O_2X_2$ и $O_2Y_2$ — проекции $O_1X_1$ и $O_1Y_1$ соответственно на плоскость $M_2$. $O_c$ — центр объектива камеры, $O_cO$ — фокусное расстояние f. $O_c-X_cY_cZ_c$ — система координат камеры, $O_w-X_wY_wZ_w$ — мировая система координат.   Вектор $O_cP$ можно выразить как $v в системе координат $O_c-X_cY_cZ_c$. _ { c } = ( x _ { p } , y _ { p } , f ) ^ { T }$。   Пусть $O_cP$ выражается как $v в системе координат $O_w-X_wY_wZ_w$. _ { c w }$, затем $v _ { c w } = R o t _ { B } ^ { W } ( \phi , \gamma , \theta ) \cdot R o t _C^ { B } ( \phi , \gamma , \theta ) \cdot { v_c }$, где $ R o t _C^ { B } ( \phi , \gamma , \theta )$ — матрица вращения из системы координат камеры в систему координат дрона, $R o t _ { B } ^ { W } ( \phi , \gamma , \theta ) $ — матрица вращения из системы координат дрона в мировую систему координат. Угол рыскания $\phi$, угол тангажа $\gamma$ и угол крена $\theta$ БПЛА могут быть измерены с помощью IMU.   Пусть $t _ { z w } = ( 0 , 0 , 1 ) ^ { T }$ — единичный вектор на оси координат $O_wZ_w$, тогда $\cos ( < v _ { c w } , t _ { z w } > ) = \frac { v _ { c w } \cdot t _ {z w } } { | v _ { c w } | |t_{ zw }| }$   Если угол между $O_cA$ и $O_wZ_w$ равен $\rho$, то: $\rho = \arccos ( < v _ { cw } , t _ { w } >)\ \ \ \rho \ \ in\ [ 0 , \pi / 2 )$   Проекция вектора $O_cP$ на плоскость $O_cX_cY_c$ равна $O_cP. ^ { \prime }$, $O_cP ^ { \prime }$ можно выразить как $v в системе координат $O_cX_cY_cZ_c$. _ { b } = ( x _ { p } , y _ { p } , 0 ) ^ { T }$。   Пусть $O_cP^ { \prime }$ выражается как $v в системе координат $O_wX_wY_wZ_w$. _ { b w }$, тогда: $v _ { b w } = R o t _ { B } ^ { W } ( \phi , \gamma , \theta ) \cdot R o t _ { C } ^ { B } ( \phi , \gamma , \theta ) \cdot { v _b }$   Пусть $t _ { x w } = ( 1 , 0 , 0 ) ^ { T }$ — единичный вектор на оси координат $O_wX_w$. но: $\cos ( < v _ { b w } , t _ { x w } > ) = \frac { v _ { b w } \cdot t _ { x w } } { | v _ { b w } | | t _ {x w}| }$   Если $O_cP^ { \prime Угол между }$ и $O_wX_w$ равен $\epsilon$, тогда $e = \arccos ( < { v }_ { b w } , t _ { x w } > )\ \ \ \epsilon\ \ in ( 0 , 2 \pi ]$   (Он пропал??? А как насчет самолета О2???)

ссылка: 1. Метод совместной реализации обнаружения и позиционирования цели с одной полезной нагрузкой БПЛА_Ван Нин 2. Целевое положение беспилотного летательного аппарата на основе платформы оптико-электронной стабилизации и сопровождения. 3、модель камеры-обскуры | Легенда об Исуогэ 4、https://python.iitter.com/other/197329.html

система координат

Часто используемые параметры эллипсоида системы координат

Единая ставка:

Первое эксцентриситет:

Второй эксцентриситет:

Универсальный поперечный Меркатор UTM

• Унифицированная поперечная проекционная система Меркатора (Универсальная Transverse Mercator,UTM）
• 60 зон точности, 58 из которых охватывают угол 6° с востока на запад.
• Существует 20 широтных зон, каждая из которых простирается на 8° с севера на юг.
• Формат координат: пояс долготы пояс широты Эдомк северу от,вЭдомПредставляет зону долготы отцентральный меридианрасстояние проекции,ик северу отПредставляет расстояниеэкваториальныйрасстояние проекции。единица为рис。
• Положения координатной оси:
  • X: Увеличение с запада на восток, называемое «движением на восток».
  • Y: увеличивается с юга на север, называется «Север».
  • Z: увеличивается снизу вверх, называется «возвышением».
  • B: Увеличение по часовой стрелке от положительной оси X вокруг оси Z.

NED

• Северо-восточная система координат (навигационная система координат)
  • Н – северная ось указывает на север земли;
  • Е – восточная ось указывает на восток Земли;
  • D – Ось Земли перпендикулярна поверхности Земли и направлена ​​вниз.

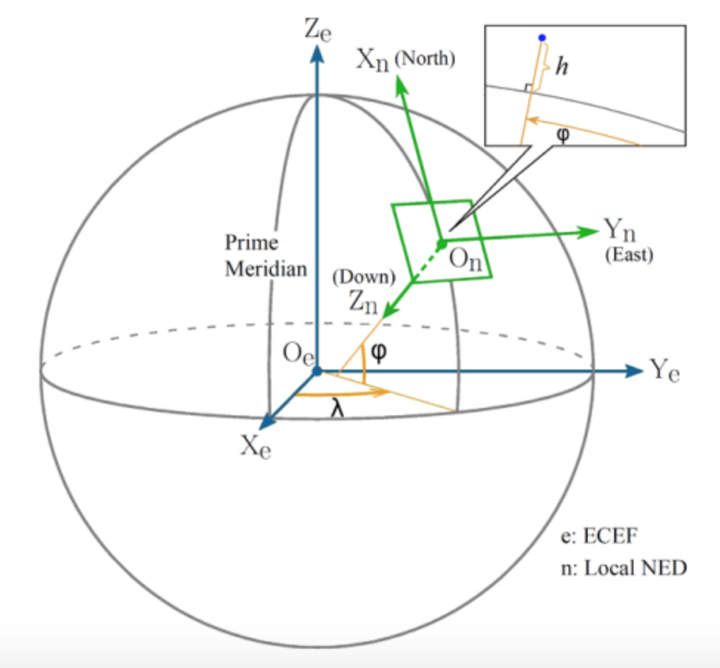
Формула преобразования координат

WGS84 <–> UTM

https://en.wikipedia.org/wiki/Universal_Transverse_Mercator_coordinate_system

Программное обеспечение для преобразования координат

COORD GM2.0 (может конвертировать 2000 координат) окончательная версия.zip - Lan Zuoyun

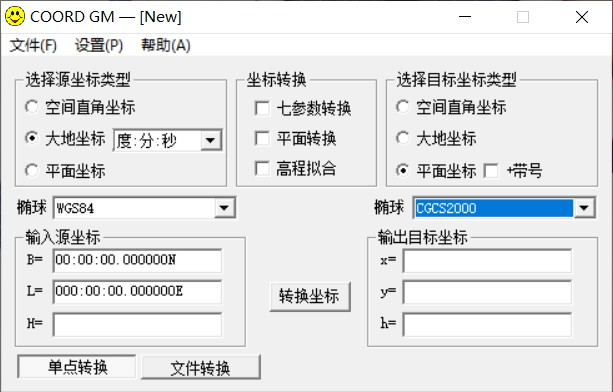
Программное обеспечение для 3D-рисования

Vectary - Build interactive 3D and AR solutions online

тестовый код

TODO

Информационная рекомендация

1、этотPPTочень хорошо：Camera Calibration

отступление

1. Обратите внимание на порядок x, y и w, h изображения в OpenCV.

# Последовательность координат точки изображения: x, y, z; и:
# row = height = Point.y
# col = width  = Point.x

# Порядок ширины и высоты изображения: высота, width, channel; и:
h = img.shape[0] - 1  # высокий
w = img.shape[1] - 1  # ширина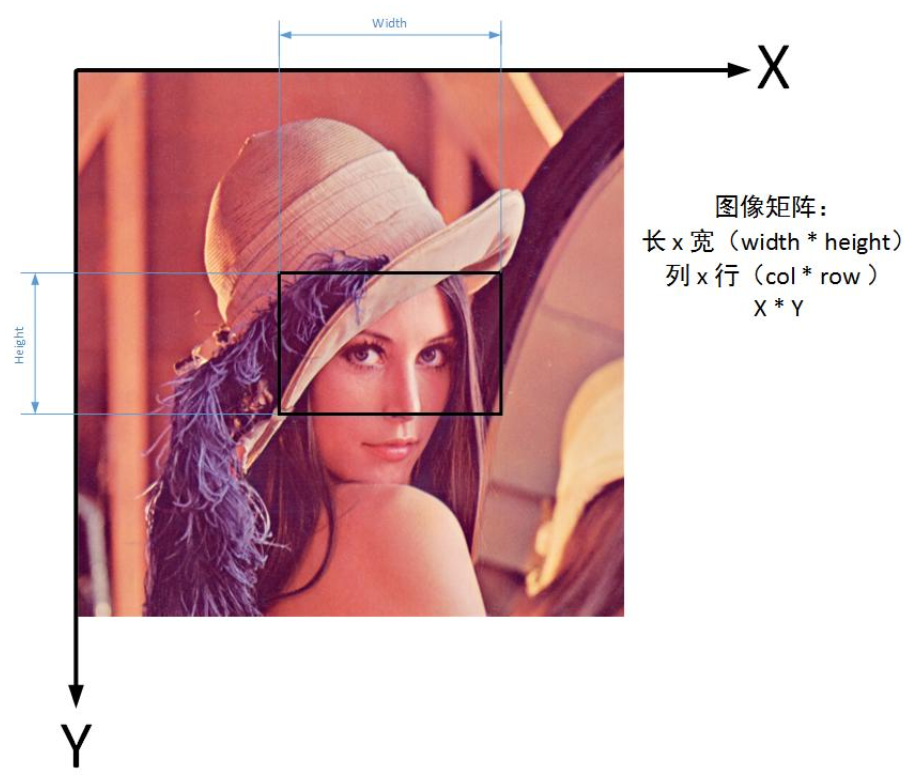

0