Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Предисловие
Приступая к глубокому обучению, выбор правильной структуры является решающим шагом. PyTorch, один из трех основных фреймворков, стал первым выбором для новичков благодаря своей простоте и удобству использования. По сравнению с другими фреймворками, PyTorch больше похож на простой в освоении язык программирования, позволяющий нам сосредоточиться на реализации функций проекта, не увязая в деталях основных принципов.
Точно так же, как когда мы пользуемся автомобилем, важнее уметь им управлять, чем тратить слишком много времени на изучение того, как устроены колеса. Я буду постепенно углублять теоретические знания и практические операции в серии статей, специально посвященных платформам глубокого обучения. Но для этого требуется определенное понимание глубокого обучения, прежде чем продолжить. На этом этапе мы сосредоточены на том, чтобы научиться гибко использовать инструмент PyTorch. Глубокое обучение включает в себя множество математических теорий и вычислительных принципов, что может быть немного обременительным для новичков. Однако, только сделав это на самом деле, мы сможем по-настоящему понять роль кода, который мы пишем в нейронной сети. Я буду усердно работать над тем, чтобы упростить знания и превратить их в знакомый контент, чтобы каждый мог понять и умело использовать структуру нейронной сети.
Если вы обнаружите, что глубокое обучение кажется трудным для понимания, я постараюсь упростить знания и преобразовать их во что-то, что нам будет легче понять. Я позабочусь о том, чтобы вы поняли полученные знания и успешно их применили. На более позднем этапе я опубликую серию статей, специально анализирующих структуру глубокого обучения, но прежде чем начать учиться, нам необходимо иметь определенную степень знакомства с теоретическими знаниями и практическими операциями глубокого обучения.
Как профессионал, занимающийся моделированием данных в течение пяти лет, я участвовал во многих проектах по математическому моделированию и понимаю принципы, процессы моделирования и методы анализа проблем различных моделей. Я надеюсь, что с помощью этой статьи вы сможете быстро освоить различные математические модели, знания машинного и глубокого обучения, а также освоить соответствующую реализацию кода. Каждая статья содержит актуальные проекты и рабочий код. Блогеры следят за различными соревнованиями по цифровому моделированию и делятся новейшими идеями и кодами, чтобы обеспечить эффективное усвоение этих знаний.
Блоггер с нетерпением ждет возможности вместе с вами изучить эту тщательно составленную колонку, полную практических проектов и работоспособного кода. Надеюсь, вы ее не пропустите.
1. Обзор VGGNet
VGGNet (Сеть группы визуальной геометрии) — это архитектура глубокой сверточной нейронной сети, предложенная Группой визуальной геометрии Оксфордского университета. Она достигла отличных результатов в задаче классификации изображений ImageNet в 2014 году. VGGNet известен, с одной стороны, своей простой и эффективной сетевой структурой, а с другой стороны, тем, что демонстрирует мощные возможности глубоких сверточных нейронных сетей посредством глубокого стека.
VGGNet исследовал взаимосвязь между глубиной сверточной нейронной сети и ее производительностью и успешно построил сверточную нейронную сеть с глубиной от 16 до 19 слоев, доказав, что увеличение глубины сети может существенно повлиять на конечную производительность сети. в определенной степени совершают ошибки. Скорость значительно снизилась, в то время как масштабируемость очень сильна, а способность к обобщению при переходе на другие данные изображения также очень хороша. До сих пор VGG все еще используется для извлечения признаков изображения.
VGGNet содержит две структуры: 16 и 19 слоев соответственно. В структуре VGGNet ядра всех сверточных слоев имеют размер всего 3*3. Причина, по которой в VGGNet постоянно используются три группы ядер 3*3, заключается в том, что это дает тот же эффект, что и использование одного ядра 7*7. Однако более глубокая структура сети также изучает более сложные нелинейные отношения, что делает модель более эффективной. Еще одним преимуществом этой операции является уменьшение количества параметров, поскольку для сверточного слоя, содержащего ядра C, исходное количество параметров равно 7*7*C, а новое количество параметров равно 3* (3*3* С).
На следующем рисунке показана конкретная структурная схема VGG16:
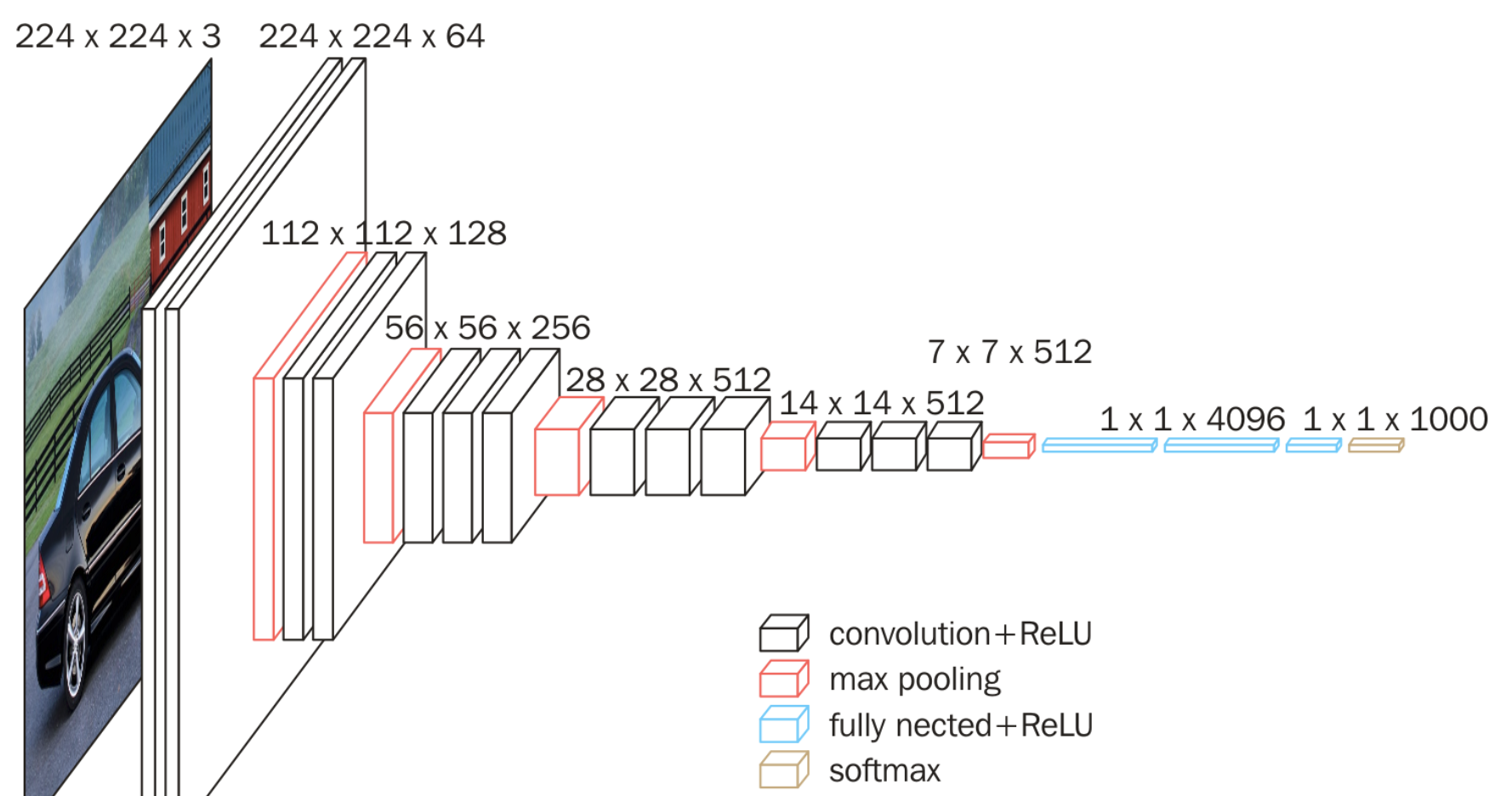
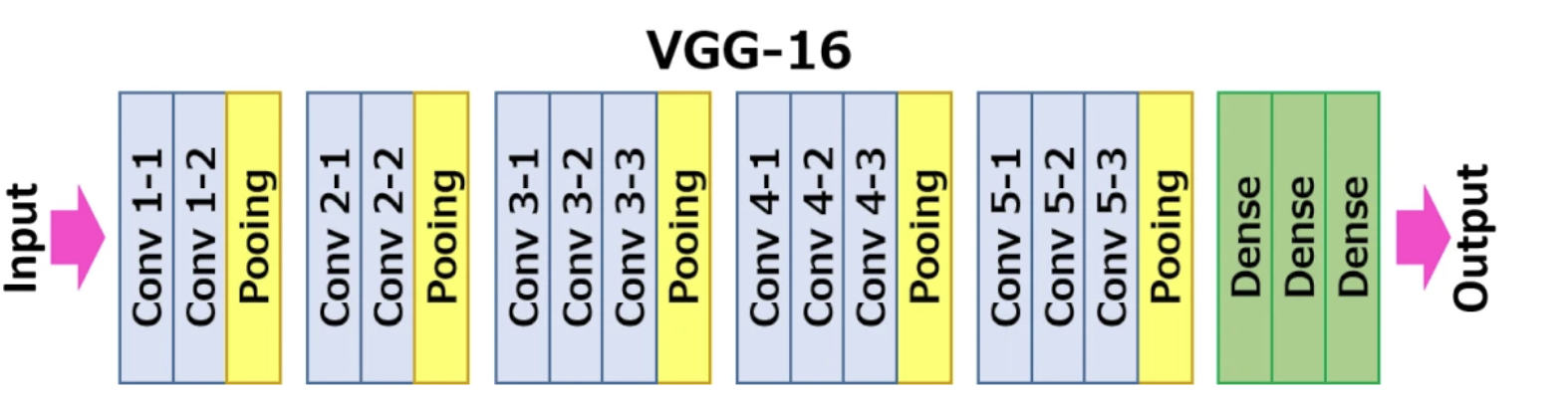
Специфический анализ на основе VGG16, включая:
- 13 сверточных слоев (Convolutional Layer)
- 3 полностью связанных слоя (Полностью связанный слой)
- 5 слоев пула (слой пула)
Среди них сверточный слой и полносвязный слой имеют весовые коэффициенты, поэтому их также называют весовыми слоями. Общее число составляет 13+3=16, что является источником 16 в VGG16.
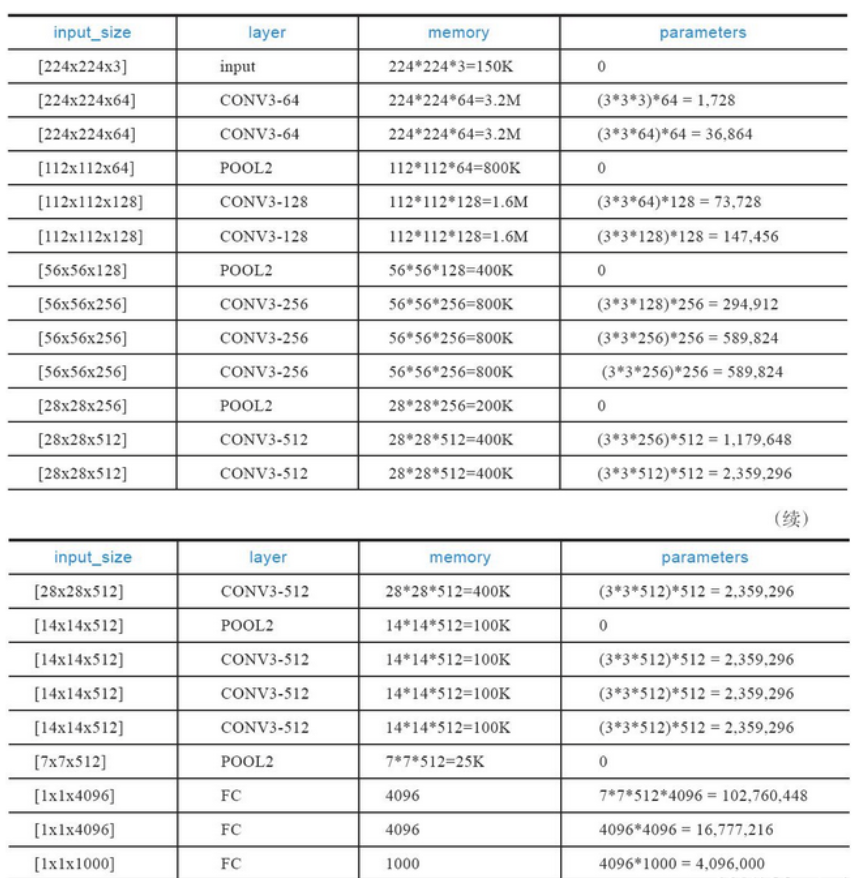
Потребление памяти в основном происходит из-за ранних сверток, тогда как увеличение размера параметра происходит на более поздних полносвязных уровнях. Из-за большого количества используемых сверточных слоев VGGNet имеет большое количество параметров, а процессы обучения и вывода требуют больше вычислительных ресурсов. Более того, количество параметров велико, и необходимо больше данных, чтобы избежать проблем переобучения.
2. Построение сети PyTorch
Мы обращаемся к приведенной выше структуре сети и используем Pytorch для построения сети. Во-первых, мы можем сначала построить выходной слой и построить его в соответствии с конкретными параметрами каждого слоя, которые я указал выше:
def __init__(self, num_classes=1000):
super(VGG,self).__init()__
self.features = self._make_layers()
self.classifier = nn.Sequential(
nn.Linear(512*7*7,4096),
nn.ReLU(True),
nn.Dropout(),
nn,Linear(4096,4096),
nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096,num_classes)
)Далее мы построим сверточные и полностью связанные слои. Мы можем использовать циклы, чтобы избежать утомительного написания слоев на каждом этапе:
def _make_layers(self):
layers = []
in_clannels = 3
cfg =[64,64,'M',128,128,'M',256,256,256,'M',512,512,512,'M']
for v in cfg:
if v =='M':
layers +=[nn.MaxPool2d(kernel_size=2,stride=2)]
else:
conv2d = nn.Conv2d(in_channels,v,kernel_size)
layers +=[conv2d,nn.ReLU(inplace=True)]
in_channels = v
return nn.Sequential(*layers)Затем напишите необходимое распространение для каждой нейронной сети:
def forward(self, x):
x = self.features(x)
x = x.view(x.size(0), -1)
x = self.classifier(x)
return xОбщая структура сети такова:
VGGNet(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace=True)
(2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace=True)
(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(6): ReLU(inplace=True)
(7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): ReLU(inplace=True)
(9): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(13): ReLU(inplace=True)
(14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): ReLU(inplace=True)
(16): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(17): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): ReLU(inplace=True)
(19): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(20): ReLU(inplace=True)
(21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(22): ReLU(inplace=True)
(23): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(classifier): Sequential(
(0): Linear(in_features=25088, out_features=4096, bias=True)
(1): ReLU(inplace=True)
(2): Dropout(p=0.5, inplace=False)
(3): Linear(in_features=4096, out_features=4096, bias=True)
(4): ReLU(inplace=True)
(5): Dropout(p=0.5, inplace=False)
(6): Linear(in_features=4096, out_features=1000, bias=True)
)
)Определим функцию потерь и метод оптимизации:
#Определить функцию потерь и метод оптимизации
criterion = nn.CrossEntropyLoss() #Определим функцию потерь: перекрестную энтропию
optimizer = torch.optim.SGD(net.parameters(),lr=0.001,импульс=0.9)#Определить метод оптимизации,стохастический градиентный спускДля обучения сверточной сети вам необходимо точно настроить исходную модель vgg. Набор данных Cifar10 имеет 10 категорий, а в матрицу преобразования изображений необходимо добавить слой адаптивного пула, что требует некоторых улучшений:
import torch.nn as nn
# Установите случайные начальные числа, чтобы обеспечить воспроизводимость экспериментов.
torch.manual_seed(0)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
class VGGNet(nn.Module):
def __init__(self, num_classes=10):
super(VGGNet, self).__init__()
self.features = self._make_layers()
self.avgpool = nn.AdaptiveAvgPool2d((7, 7))
self.classifier = nn.Sequential(
nn.Linear(512*7*7,4096),
nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096,4096),
nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096,num_classes)
)
def _make_layers(self):
layers = []
in_channels = 3
cfg =[64,64,'M',128,128,'M',256,256,256,'M',512,512,512,'M',512, 512, 512, 'M']
for v in cfg:
if v =='M':
layers +=[nn.MaxPool2d(kernel_size=2,stride=2)]
else:
conv2d = nn.Conv2d(in_channels,v,kernel_size=3, padding=1)
layers +=[conv2d,nn.ReLU(inplace=True)]
in_channels = v
return nn.Sequential(*layers)
def forward(self, x):
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.classifier(x)
return xСледует отметить, что нам необходимо инициализировать веса сети. Если веса не обновляются, вероятность 10 000 изображений и фактической картинки, угаданной без помощи алгоритма, будут согласованы. сеть:
for epoch in range(1):
train_loss=0.0
for batch_idx,data in enumerate(train_loader,0):
#инициализация
inputs,labels = data #Получить данные
inputs = inputs.to(device)
labels = labels.to(device)
optimizer.zero_grad() #Градиент установлен на 0
#Процесс оптимизации
outputs = net(inputs) #Введите данные в сеть и получите результаты прогнозирования первого раунда прямого распространения сети
loss = criterion(outputs,labels) #Результаты прогнозирования и метки рассчитывают потери с помощью ранее определенной перекрестной энтропии.
loss.backward() #Обратное распространение ошибки
optimizer.step() #Весовые коэффициенты оптимизации стохастического градиентного спуска
#Просмотр состояния обучения сети
train_loss += loss.item()
if batch_idx % 2000 == 1 :
print(batch_idx)
print('[%d,%5d] loss: %.3f' % (epoch + 1,batch_idx + 1,train_loss / 2000))
train_loss = 0.0
print('Saving epoch %d model ...'%(epoch + 1))
state = {
'net':net.state_dict(),
'epoch':epoch+1,
}
if not os.path.isdir('checkpoint'):
os.mkdir('checkpoint')
#torch.save(state,'./checkpoint/cifar10_epoch_%d.ckpt'%(epoch+1))
print('Finished Training')Затем мы вычисляем эффект прогнозирования всего тестового набора:
#Пакетный расчет эффекта прогнозирования всего набора тестов
correct= 0
total = 0
with torch.no_grad():
for data in test_loader:
images,labels = data
images = images.to(device)
labels = labels.to(device)
outputs = net(images)
_,predicted = torch.max(outputs.data,1)
total += labels.size(0)
correct += (predicted == labels ).sum().item() #Если тип помеченной метки соответствует прогнозируемому типу, он считается правильным и засчитывается.
print('Accurary of the network on the 10000 test images : %d %%'%(100*correct/total))Очевидно, что вероятность точно такая же, как и фактическое предположение. Всего десять категорий 1/10 являются нормальными:
Accurary of the network on the 10000 test images : 10 %Перед обучением нам необходимо инициализировать веса сети:
def initialize_weights(module):
if isinstance(module, nn.Conv2d):
nn.init.kaiming_normal_(module.weight, mode='fan_out', nonlinearity='relu')
if module.bias is not None:
nn.init.constant_(module.bias, 0)
elif isinstance(module, nn.Linear):
nn.init.normal_(module.weight, 0, 0.01)
nn.init.constant_(module.bias, 0)Тогда в версии прогнозирования обучения:
Accurary of the network on the 10000 test images : 47 %Эффект очень очевиден.
Если есть какие-либо ошибки, пожалуйста, оставьте сообщение для консультации. Большое спасибо.
Это все по этому вопросу. Меня зовут фанат. Если у вас есть вопросы, оставьте сообщение для обсуждения. Увидимся в следующем выпуске.

Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.

Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).

Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)

Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.

Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
Идеальная интеграция Cursor и DeepSeek API

DeepSeek V3 снижает затраты на обучение больших моделей

Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).

DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».

Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.

Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле

Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.

9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать

Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.

Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)

50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.

Cloud Native|Практика: установка Dashbaord для K8s, графика неплохая

Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности

MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.

Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.

Центр конфигурации————Накос

Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще

[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64

Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике

Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах

Feiniu fnos использует Docker для развертывания личного блокнота Notepad

Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов

[Зона легкого облачного игрового сервера] Управление игровыми архивами


