Старший архитектор программного обеспечения: Маккейб, цикломатическая сложность
1. Объяснение концепции
Метод Мак Кейба — это способ расчета сложности программного обеспечения. Он в основном измеряет сложность кода путем подсчета количества циклов в графе потока управления программы (CFG). Его основным индикатором является цикломатическая сложность, которая используется для оценки сложности программы, ее тестируемости и ремонтопригодности. Конкретная формула расчета выглядит следующим образом:

в:
- (E) представляет количество ребер (Edges) в графе.
- (N) представляет количество узлов (Узлов) в графе.
- ( P ) количество, которое представляет диаграмму подключенных количество компонентов (обычно 1 для одной программы).
Вот конкретные шаги:
- Нарисуйте граф потока управления: Используйте каждый базовый блок программы (часть кода, выполняемую последовательно) в качестве узла, а передачу потока управления (например, условный переход, переход из цикла) в качестве ребра для построения графа потока управления.
- Подсчитайте количество узлов ( N ): статистика Общее количество узлов в графе потока управления.
- Вычислите количество ребер ( E ): статистика контролирует общее количество ребер в потоковом графе.
- Определим количество связных компонентов ( P ): Обычно это 1 для одной программы или количество подграфов статистики, если имеется несколько связанных подграфов.
- Примените формулу для расчета цикломатической сложности: Использовать формулу ( CC = E - N + 2P ) Вычислите цикломатическую сложность.
Пример
Предположим следующий псевдокод:
if (condition1) {
// block A
} else {
// block B
}
// block C
while (condition2) {
// block D
}Схема управления выглядит следующим образом:
- Количество узлов ( N = 4 ) (A, B, C, D)
- Количество сторон ( E = 5 )(condition1 -> A, condition1 -> B, A -> C, B -> C, C -> D, D -> C)
- Количество связанных компонентов ( P = 1 )
Расчет цикломатической сложности:
[ CC = E - N + 2P = 6 - 4 + 2 = 4 ]
Это указывает на то, что цикломатическая сложность этого кода равна 4.
Чем выше цикломатическая сложность, тем выше сложность кода и потенциальная сложность обслуживания. В общем, цикломатическую сложность лучше всего поддерживать на низком уровне, чтобы улучшить читаемость и удобство сопровождения кода.
2. Название
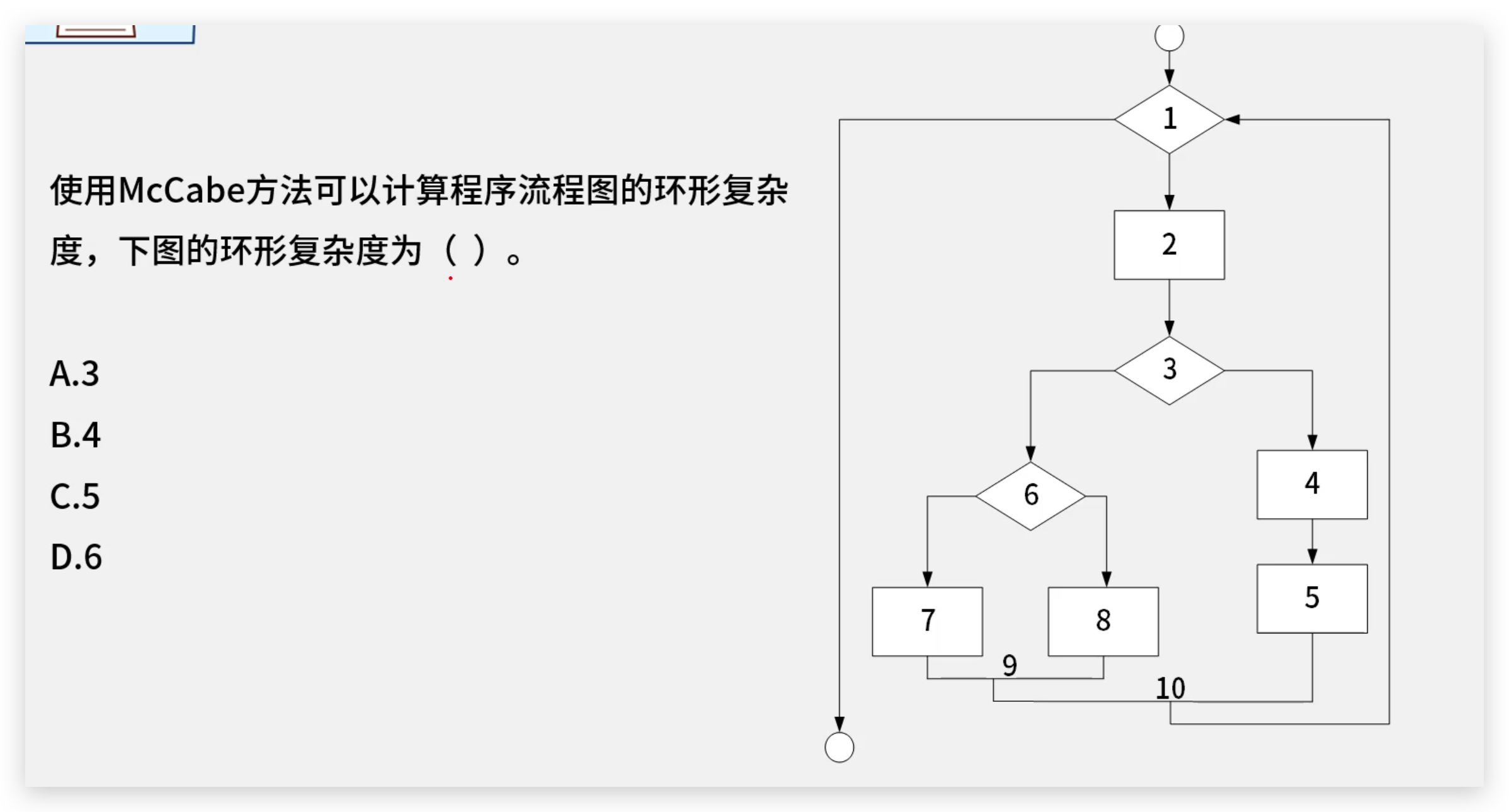
Объединенное место должно дополнять узлы, поэтому 9 и 10 должны дополнять два узла. Обратите внимание, что начало и конец также являются узлами.
Следовательно, всего 14 ребер — 12 узлов +2 = 4, выбор Б.

Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.

Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).

Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)

Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.

Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
Идеальная интеграция Cursor и DeepSeek API

DeepSeek V3 снижает затраты на обучение больших моделей

Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).

DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».

Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.

Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле

Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.

9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать

Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.

Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)

50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.

Cloud Native|Практика: установка Dashbaord для K8s, графика неплохая

Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности

MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.

Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.

Центр конфигурации————Накос

Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще

[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64

Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике

Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах

Feiniu fnos использует Docker для развертывания личного блокнота Notepad

Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов

[Зона легкого облачного игрового сервера] Управление игровыми архивами


