NHWC и NCHW — широко используемые форматы данных в сверточных нейронных сетях (CNN). Они определяют, как многомерные данные, такие как изображения, облака точек или карты объектов, хранятся в памяти.

• NHWC (количество образцов,высокий,ширина,канал): Этот формат хранилища данных канала в конце,Это формат TensorFlow по умолчанию.
• NCHW (количество выборок, каналов, высота, ширина): каналы предшествуют размерам высоты и ширины, часто используются с PyTorch.

Повлияет ли выбор между NHWC и NCHW на доступ к памяти и эффективность вычислений? В этой статье мы попытаемся проиллюстрировать эту проблему на примере производительности модели и использования оборудования.

Свертка как GEMM

GENeral Matrix to Matrix Multiplication (матричное умножение общих матриц)

Свертку можно реализовать с помощью метода, основанного на преобразовании, такого как быстрое преобразование Фурье, которое преобразует свертку в поэлементное умножение в частотной области, или с использованием метода без преобразования, такого как матричное умножение, где входные данные и фильтр (ядро свертки) планаризуются и объединяются с использованием матричных операций для вычисления выходной карты объектов.

Но: fft требуют большого объема памяти, поскольку для хранения преобразованной матрицы требуется дополнительная память. А БПФ требует больших вычислительных затрат, особенно при преобразовании данных туда и обратно между временной и частотной областью, что связано с операционными издержками.

Общее матричное умножение операции свертки выглядит следующим образом. Каждое восприимчивое поле складывается по столбцам для получения матрицы преобразования сопоставления признаков. При этом матрица фильтра сглаживается и накладывается построчно, образуя матрицу преобразования фильтра. Матрицы преобразования фильтрации и преобразования объектов подвергаются умножению матриц для формирования сплющенной выходной матрицы. Матрица преобразования здесь представляет собой промежуточную матрицу, которая представляет собой просто числовую перестановку и не имеет ничего общего с преобразованием в частотной области.

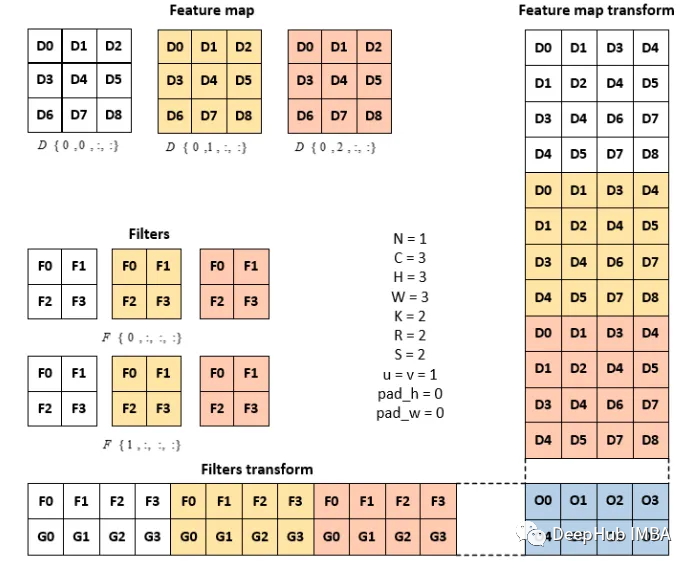
N - размер пакета карт объектов, C - входные каналы, h - высота ввода, W - ширина ввода,

k - выходной канал, r - высота фильтра, s - ширина фильтра, p - высота выхода, q - ширина выхода

Матрица преобразования карты признаков и матрица преобразования фильтра рассматриваются как промежуточные матрицы, размеры которых больше, чем сама карта признаков. Размер карты объектов = C × H × W, (3x3x3). Размер преобразования карты объектов = CRS × NPQ (12x4).

Реализация GEMM на графическом процессоре:

Графический процессор использует неявный GEMM, чтобы избежать нехватки памяти. В неявном GEMM вместо формирования матрицы преобразования каждый столбец и строка индексируются динамически. Конечный результат сохраняется непосредственно в соответствующем индексе выходного тензора.

Графические процессоры, состоящие из SM (потоковых мультипроцессоров), в основном используются для выполнения параллельных вычислений. В приведенном выше неявном GEMM каждое матричное умножение можно разделить на более мелкие матричные умножения или блоки. Затем каждый блок обрабатывается SM одновременно, чтобы ускорить процесс.

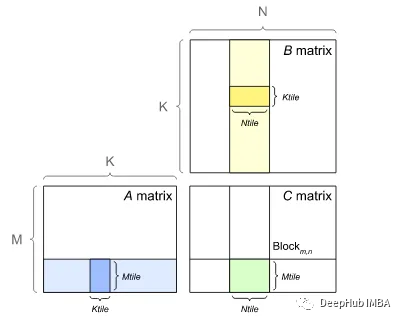
В рамках описанного выше процесса вычислений также необходимо сохранить тензоры. Давайте посмотрим, как тензоры хранятся в графическом процессоре.

Тензоры обычно хранятся на графическом процессоре в разнесенном формате, где элементы хранятся несмежно в макете памяти. Этот метод хранения перекрестных строк обеспечивает гибкость организации тензоров в различных режимах (например, в формате NCHW или NHWC), оптимизируя доступ к памяти и эффективность вычислений.

Учитывая тензоры, как показано на рисунке ниже, мы можем представить их в формате NCHW и NHWC, где элементы тензора упорядочиваются в памяти, сохраняя каждую строку последовательно.

NCHW

Здесь W — наиболее динамичное измерение. Элементы одного и того же канала сохраняются вместе, за ними следуют элементы следующего канала.

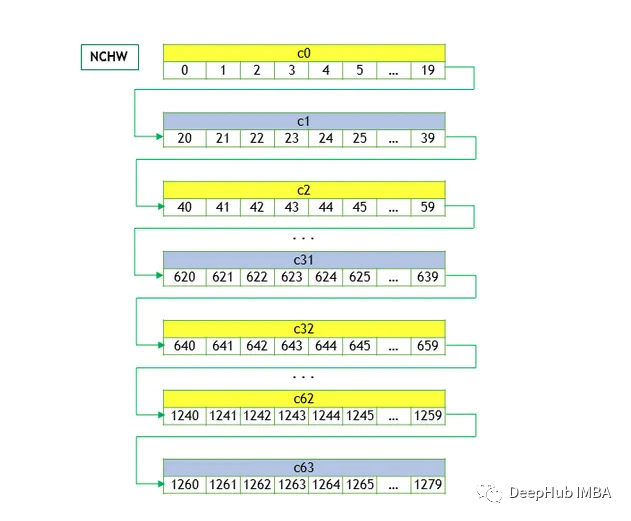
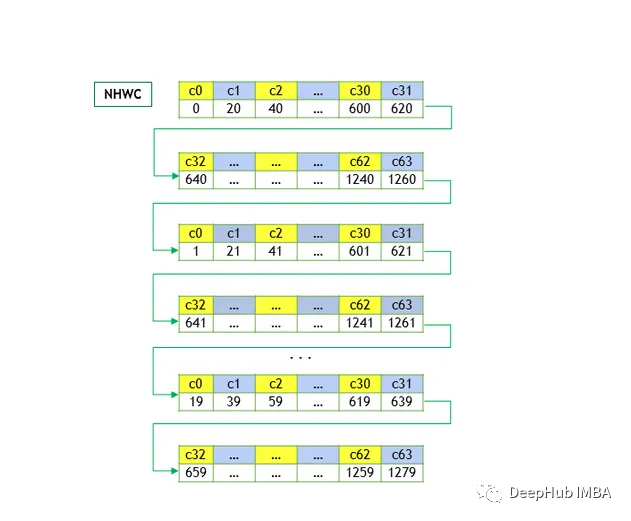
NHWC

Здесь C — динамический размер. Элементы из одного и того же пространственного местоположения во всех каналах сохраняются последовательно, за ними следуют элементы из следующего пространственного местоположения, что оптимизирует доступ к пространственным данным в каждом канале.

Пропускная способность памяти на графическом процессоре

Графические процессоры — это высокопараллельные процессоры, которые лучше всего работают, когда доступ к данным осуществляется объединенным способом, то есть им нравится считывать данные последовательным и организованным образом. Когда каждый поток ищет данные в кэше L2, если это попадание в кэш (содержимое запрошенной памяти доступно в кэше), доступ к памяти происходит быстро. В случае промаха в кэше (отрицания попадания в кэш) графический процессор обращается к DRAM для получения содержимого запрошенного адреса памяти, что является трудоемкой операцией.

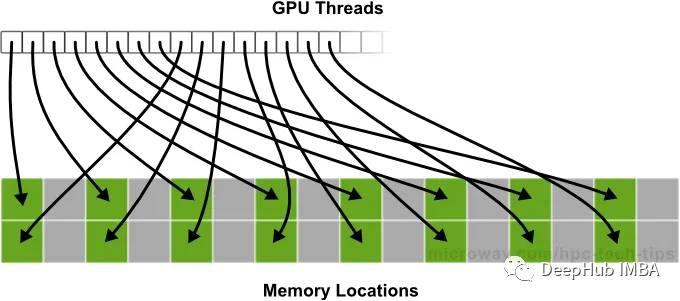
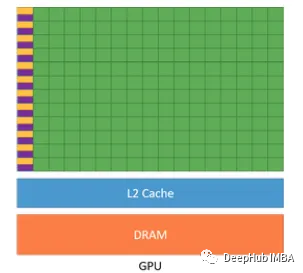
Когда графическому процессору необходимо получить доступ к данным, хранящимся в памяти, он делает это в рамках «транзакции». В зависимости от конфигурации графического процессора каждая транзакция обращается к 32/128 байтам информации. Доступная информация остается в кэше. Когда другой поток графического процессора запрашивает доступ к памяти, он сначала проверяет кеш. Если данные недоступны в кэше, запрос будет перенаправлен в DRAM.

Принцип работы графического процессора очень сложен. Мы не хотим и не имеем времени подробно объяснять его здесь, поэтому кратко резюмируем его так:

Транзакции объединенной памяти происходят, когда графический процессор обращается к памяти в смежных блоках. Если графическому процессору необходимо прочитать 32 байта данных, хранящихся в памяти последовательно, он выполнит одну объединенную транзакцию памяти, чтобы получить все 32 байта одновременно. Необъединенные транзакции с памятью происходят, когда графическому процессору требуется доступ к данным, которые не хранятся в памяти последовательно. В этом случае графическому процессору потребуется выполнить несколько транзакций для получения всех необходимых данных.

В случае GEMM, независимо от высоты и ширины фильтра, мы можем гарантировать, что будет считана вся информация о канале для данного пространственного местоположения. Например, если наши входные объекты имеют размер 128 x 128 x 32. Независимо от того, используем ли ядра 1x1 или 3x3, мы можем читать все каналы в позиции (1,1).

При использовании NCHW, который хранит все элементы, принадлежащие одному каналу, вместе, нам пришлось бы выполнить свертку 1x1 между позициями a[0], a[16384], a[32,768]... до позиции a[16384x31]. Эти местоположения не являются смежными и определенно вызовут промахи в кэше, что приведет к дополнительным накладным расходам при чтении памяти. Остальные данные, считанные во время каждой транзакции, также не используются, что также известно как транзакция с несвязанной памятью.

При использовании формата NHWC для представления тензоров местоположениями доступа являются a[0], a[1]..., a[127], которые являются последовательными и определенно являются попаданиями в кэш. Первый доступ к a[0] приводит к промаху в кэше и транзакции по выборке 32/128 байтов данных из DRAM. При обращении к [1] ​​это будет попадание в кэш, сохраняющее транзакцию. Даже если промах в кэше приводит к транзакции из DRAM после определенного количества ячеек, сама транзакция будет содержать непрерывные данные для смежных ячеек памяти, которые могут быть кэшированы при доступе к дальнейшим ячейкам, что называется транзакцией объединенной памяти.

NHWC уменьшает узкое место доступа к памяти графических процессоров с ядром Zhang, тем самым оптимизируя производительность. По сравнению с NCHW он кажется лучшим выбором.。

Ниже приведены показатели производительности TFLOPS для NCHW и NHCW под NVIDIA A100-SXM4-80GB, CUDA 11.2, cuDNN 8.1. Мы видим, что NHWC работает лучше с точки зрения TFLOPS в обеих настройках. Для простоты мы не будем здесь рассматривать схему NC/xHWx, которая представляет собой вариант NHWC, подготовленный для операций с тензорным ядром NVIDIA.

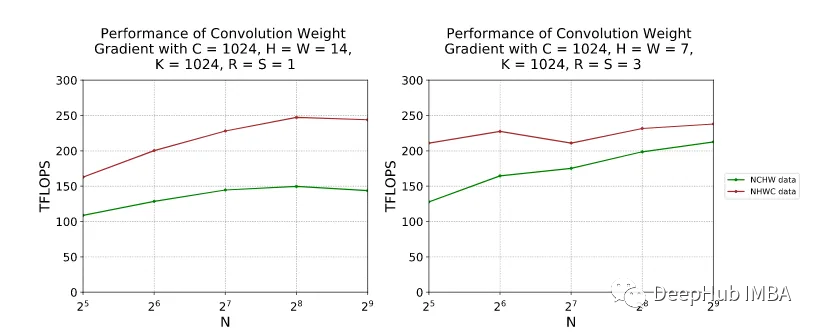
Так почему же Pytorch до сих пор использует NCHW?

В качестве ссылки можно использовать сообщение на официальном форуме:

https://discuss.pytorch.org/t/why-does-pytorch-prefer-using-nchw/83637

Кроме того, об этом также говорится на официальном сайте TensorFlow, который также можно использовать в качестве справочного материала.

Most TensorFlow operations used by a CNN support both NHWC and NCHW data format. On GPU, NCHW is faster. But on CPU, NHWC is sometimes faster.

Ссылки

1. https://docs.nvidia.com/deeplearning/performance/dl-performance-convolutional/index.html#imp-gemm-dim
2. https://docs.nvidia.com/deeplearning/cudnn/developer-guide/index.html
3. https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html
4. https://leimao.github.io/blog/CUDA-Convolution-Tensor-Layouts/
5. https://www.microway.com/hpc-tech-tips/avoiding-gpu-memory-performance-bottlenecks/
6. https://stackoverflow.com/questions/44280335/how-much-faster-is-nchw-compared-to-nhwc-in-tensorflow-cudnn

Автор: Дипика