[Сложная сеть] Модель распространения эпидемии - SI, SIS, SIR (включая примеры) [python]
[Комплексная сеть] Модель распространения эпидемии — SI, SIS, SIR [python]
1. Концепция распространения эпидемии
- Восприимчивый (S): Лица, которые еще не были инфицированы этой болезнью;
- Инфицированные (I): Лица, инфицированные этим заболеванием и способные заразить;
- Выздоровевшие (R): Лица, которые приобрели постоянный иммунитет после излечения или умерли из-за болезни.
2. Модель распространения эпидемии
2.1 Набор данных модели
2.1.1 Набор данных
Набор данных представляет собой граф связей, состоящий из 200 узлов, который можно понимать как сообщество из 200 человек. Каждый человек имеет свою собственную взаимосвязь (называемую соседними узлами).

2.1.2 Импорт и рисование данных
Код 👇
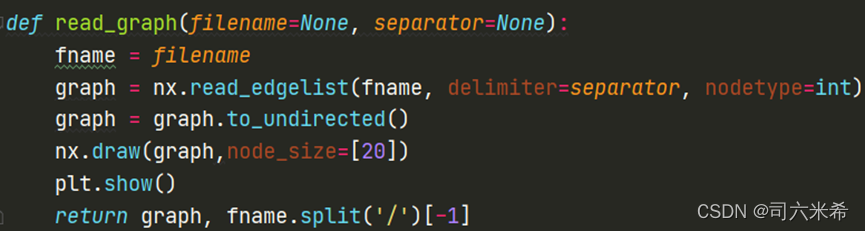
2.1.3 Сетевая диаграмма набора данных

2.2 Модель СИ
Как только узел переходит из состояния S в состояние I, он всегда будет в состоянии I. Используется для описания болезней, которые невозможно вылечить после заражения, или эпидемий, при которых отсутствует эффективный контроль над внезапными вспышками.
2.2.1 Идеи реализации
- Создать словарь S, I (используется для хранения обычных узлов + зараженных узлов)
- Инициализируйте случайные начальные числа и сохраните список случайных начальных чисел в файлеseed_list как зараженный набор.
- Получить соседей зараженного человека [соседние узлы будут заражены с определенной вероятностью]
- Добавить новых зараженных людей, выбранных случайным образом, в словарь I [Зараженные лица] Уменьшить количество новых зараженных людей, выбранных случайным образом в словаре S [нормальные люди]
- Обновить новых нормальных людей и зараженных людей [рассчитать выживаемость]
- Пока нормальный не равен 0, программа завершается
2.2.2 Код
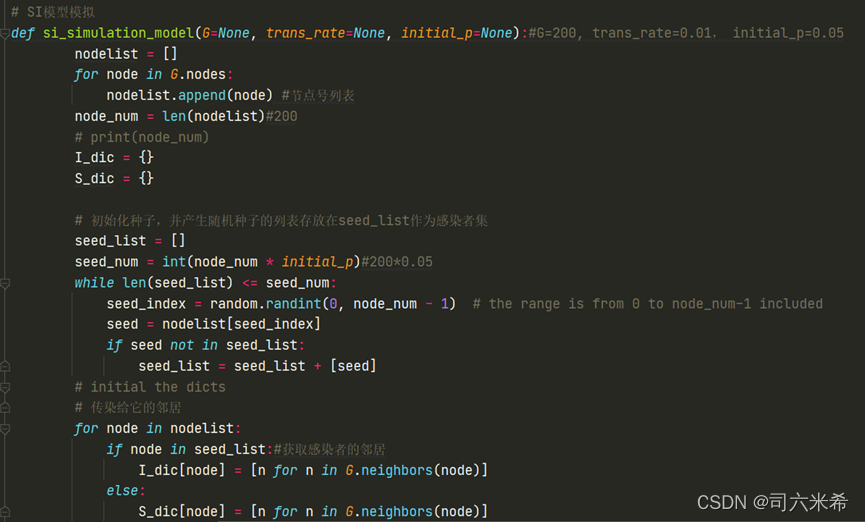
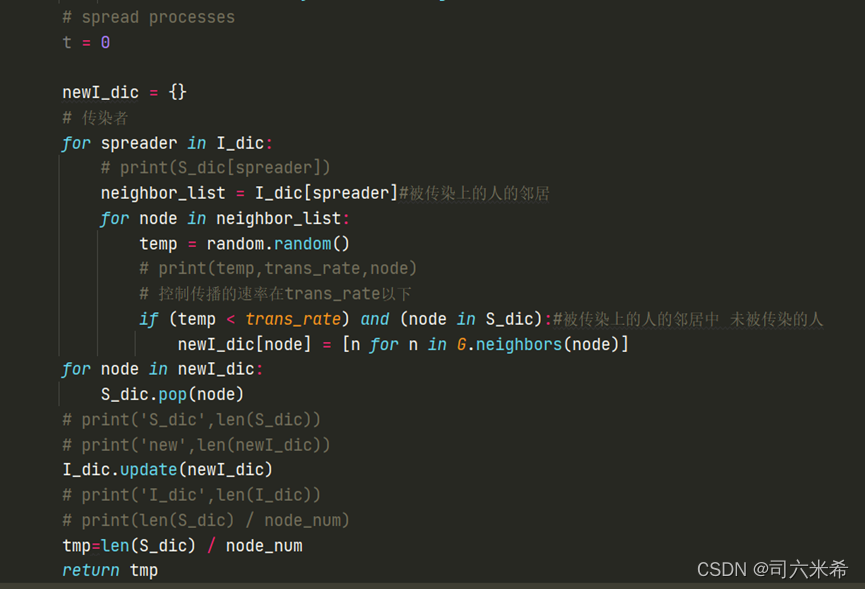
Расчет выживаемости👇
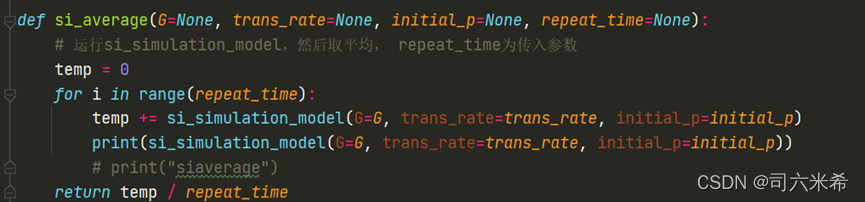
2.2.3 Результаты
SI👇
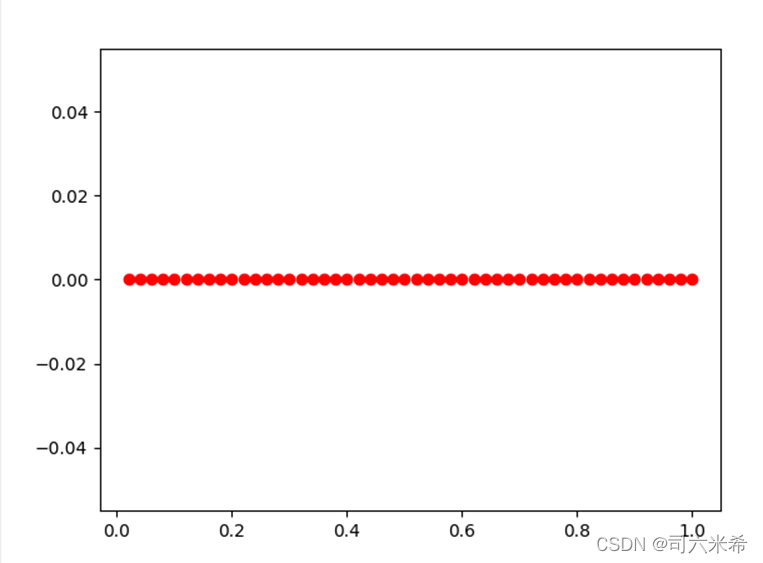
Улучшения рисования СИ 👇 Потому что 0,00 на рисунке выше означает, что в цикле while для рисования изображения будет возвращен только S_dic, когда все заражены, поэтому независимо от того, сколько раз цикл повторяется, в качестве конечного результата будет возвращено 0,00. изменилось на новое изображение следующим образом
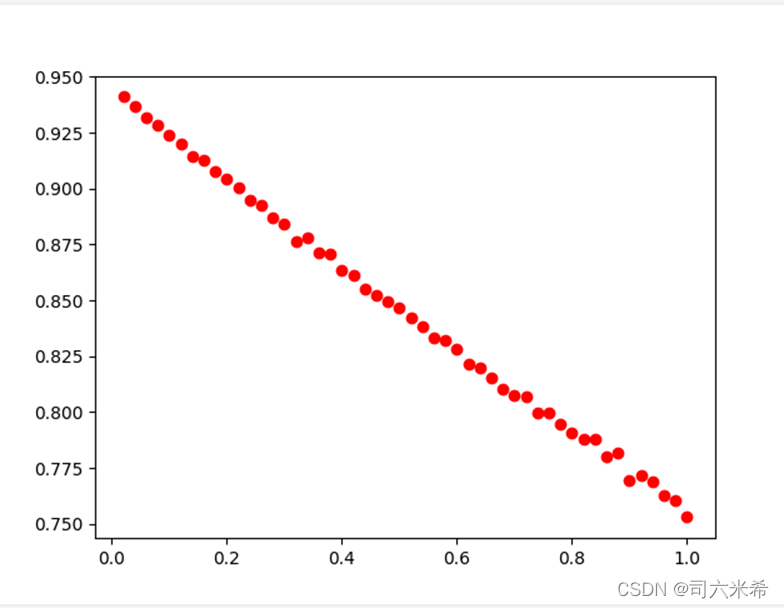
2.3 Модель SIS
После того, как узел в состоянии S контактирует с узлом в состоянии I, он перейдет в состояние I с вероятностью λ. В то же время узел в состоянии I также вернется в состояние S с вероятностью . γ.
2.3.1 Идеи реализации
- Об идее внедрения SIМодель База,Добавьте параметр rekov_rate [вероятность восстановления_rate заключается в том, что зараженный человек вернется к нормальному состоянию],Реализуйте преобразование из I в S
- Обновить новых нормальных людей и зараженных людей [рассчитать выживаемость]
2.3.2 Код
Просто измените его в соответствии с 2.2.
2.3.3 Результаты
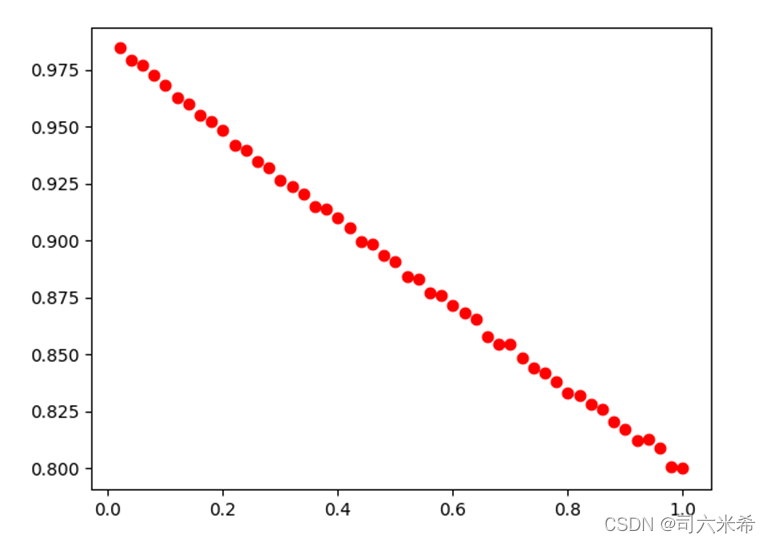
2.4 Модель СИР
После того, как узел в состоянии S контактирует с узлом в состоянии I, он перейдет в состояние I с вероятностью λ, а узел в состоянии I перейдет в состояние R с вероятностью γ.
2.4.1 Идеи реализации
- Об идее внедрения SIМодель База,Добавьте параметр Recov_rate [Вероятность восстановления_скорости здесь означает, что зараженный человек перейдет в состояние выздоровления],Реализуйте преобразование I в R
- Обновление новых нормальных людей, инфицированных и выздоровевших людей [рассчитать выживаемость]
2.4.2 Код
Просто измените его в соответствии с 2.2.
2.4.3 Результаты
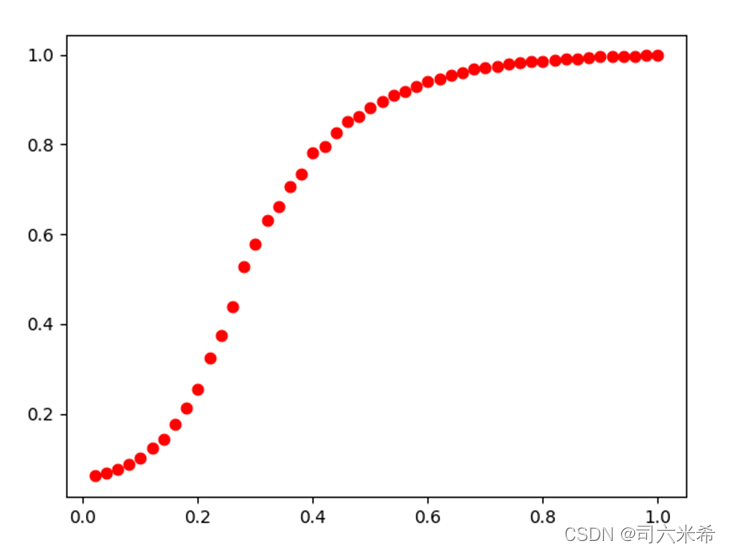

Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.

Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).

Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)

Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.

Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
Идеальная интеграция Cursor и DeepSeek API

DeepSeek V3 снижает затраты на обучение больших моделей

Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).

DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».

Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.

Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле

Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.

9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать

Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.

Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)

50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.

Cloud Native|Практика: установка Dashbaord для K8s, графика неплохая

Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности

MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.

Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.

Центр конфигурации————Накос

Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще

[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64

Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике

Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах

Feiniu fnos использует Docker для развертывания личного блокнота Notepad

Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов

[Зона легкого облачного игрового сервера] Управление игровыми архивами


