Радиолокационное обнаружение и моделирование MATLAB
Радиолокационное обнаружение и моделирование MATLAB

Предисловие

В этой статье представлено содержание радиолокационного обнаружения в виде карты связей и объяснена реализация части моделирования.

1. Радиолокационное обнаружение

Интеллект-карта показана ниже. Если она вам нужна, перейдите в конец статьи, чтобы получить ее.

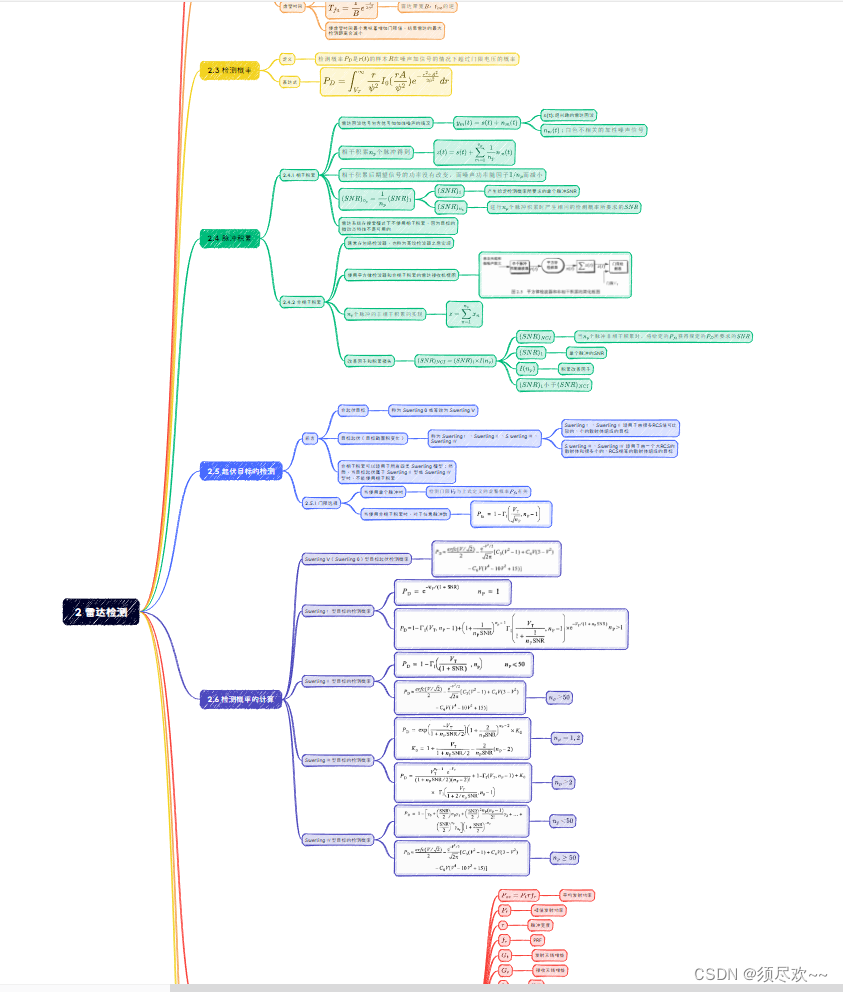
2. Моделирование в Matlab

1. Функции плотности вероятности Гаусса и Рэлея.

Функция плотности вероятности Рэлея:

f(x)=\frac{x}{\sigma^2}e^{-\frac{x^2}{2\sigma^2}}

Гауссова функция плотности вероятности:

f(x) \approx \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
x

это переменная,

\mu

это среднее значение,

\sigma

это дисперсия

①, исходный код MATLAB
Язык кода:javascript
копировать
clear all
close all
xg = linspace(-6,6,1500); % randowm variable between -4 and 4
xr = linspace(0,6,1500); % randowm variable between 0 and 8
mu = 0; % zero mean Gaussain pdf mean
sigma = 1.5; % standard deviation (sqrt(variance) 
ynorm = normpdf(xg,mu,sigma); % use MATLAB funtion normpdf
yray = raylpdf(xr,sigma); % use MATLAB function raylpdf
plot(xg,ynorm,'k',xr,yray,'k-.');
grid
legend('Gaussian pdf','Rayleigh pdf')
xlabel('x')
ylabel('Probability density')
gtext('\mu = 0; \sigma = 1.5')
gtext('\sigma =1.5')
②. Моделирование.

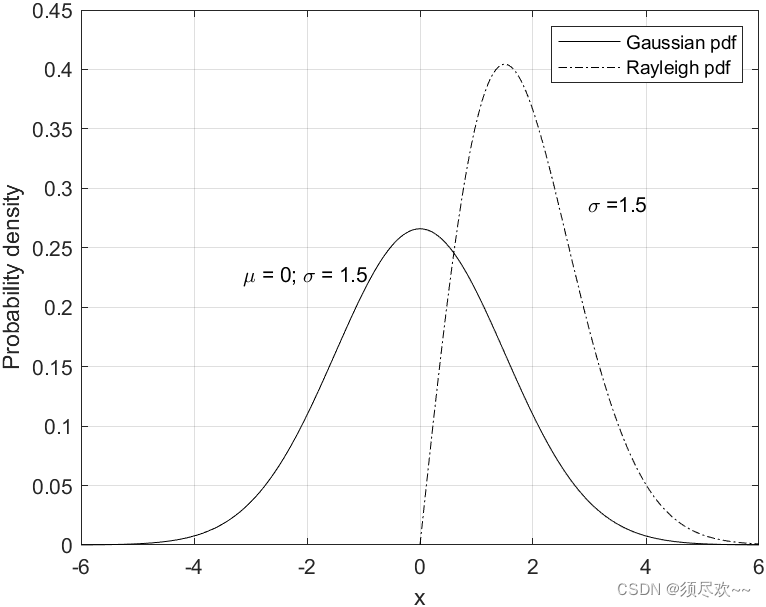
Плотности вероятности Гаусса и Рэлея

2. Кривая нормированного порога относительно вероятности ложной тревоги.

Вероятность ложной тревоги:

P_{fa}=e^{\frac{-V_T^2}{2\psi^2}}

Пороговое напряжение:

V_T=\sqrt{2\psi^2ln(\frac{1}{P_{fa}})}

Примечание:

V_T

пороговое напряжение,

\psi^2

это дисперсия

①, исходный код MATLAB
Язык кода:javascript
копировать
close all
clear all
logpfa = linspace(.01,250,1000);
var = 10.^(logpfa ./ 10.0);
vtnorm =  sqrt( log (var));
semilogx(logpfa, vtnorm,'k')
grid
②. Моделирование.

Абсцисса

log(1/P_{fa})

Ордината

\frac{V_T}{\sqrt{2\psi^2}}

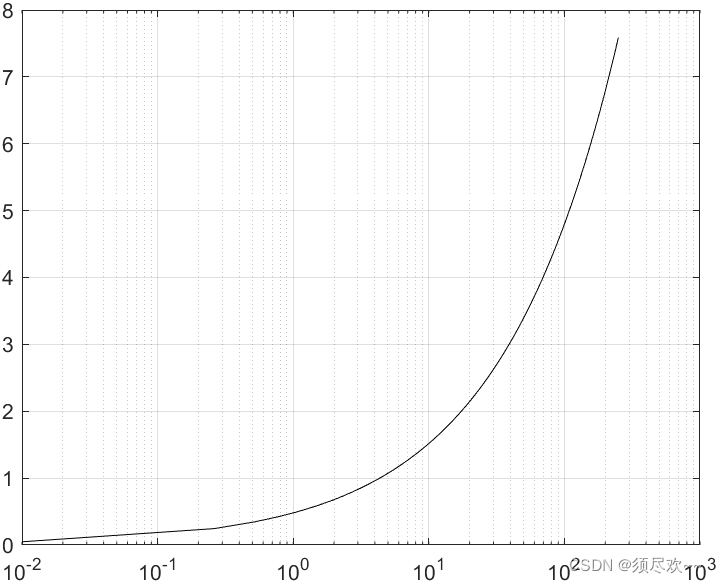
Нормализованный порог обнаружения в зависимости от вероятности ложной тревоги

Из рисунка хорошо видно, что

P_{fa}

Очень чувствителен к небольшим изменениям порогового значения.

3. Кривая зависимости вероятности обнаружения относительно отношения сигнал/шум одиночного импульса

вероятность обнаружения

P_D

：

Q

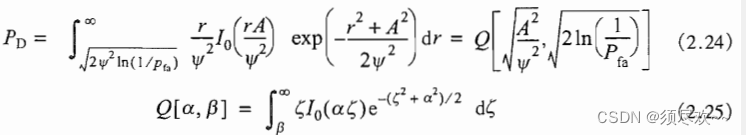
называется

Marcum Q

функция.

①, исходный код MATLAB

marcumsq.m

Язык кода:javascript
копировать
function PD = marcumsq (a,b)
% This function uses Parl's method to compute PD
max_test_value = 5000.; 
if (a < b)
   alphan0 = 1.0;
   dn = a / b;
else
   alphan0 = 0.;
   dn = b / a;
end
alphan_1 = 0.;
betan0 = 0.5;
betan_1 = 0.;
D1 = dn;
n = 0;
ratio = 2.0 / (a * b);
r1 = 0.0;
betan = 0.0;
alphan = 0.0;
while betan < 1000.,
   n = n + 1;
   alphan = dn + ratio * n * alphan0 + alphan;
   betan = 1.0 + ratio * n * betan0 + betan;
   alphan_1 = alphan0;
   alphan0 = alphan;
   betan_1 = betan0;
   betan0 = betan;
   dn = dn * D1;
end
PD = (alphan0 / (2.0 * betan0)) * exp( -(a-b)^2 / 2.0);
if ( a >= b)
   PD = 1.0 - PD;
end
return

prob_snr1.m

Язык кода:javascript
копировать
% This program is used to produce Fig. 2.4
close all
clear all
for nfa = 2:2:12
   b = sqrt(-2.0 * log(10^(-nfa)));
   index = 0;
   hold on
   for snr = 0:.1:18
      index = index +1;
      a = sqrt(2.0 * 10^(.1*snr));
      pro(index) = marcumsq(a,b);
   end
   x = 0:.1:18;
   set(gca,'ytick',[.1 .2 .3 .4 .5 .6  .7 .75 .8 .85 .9 ...
         .95 .9999])
   set(gca,'xtick',[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18])

   loglog(x, pro,'k');
end
hold off
xlabel ('Single pulse SNR - dB')
ylabel ('Probability of detection')
grid
②. Моделирование.

Вероятность обнаружения относительно одиночного импульса

SNR

Кривая отношений для

P_{fa}

ценностей:

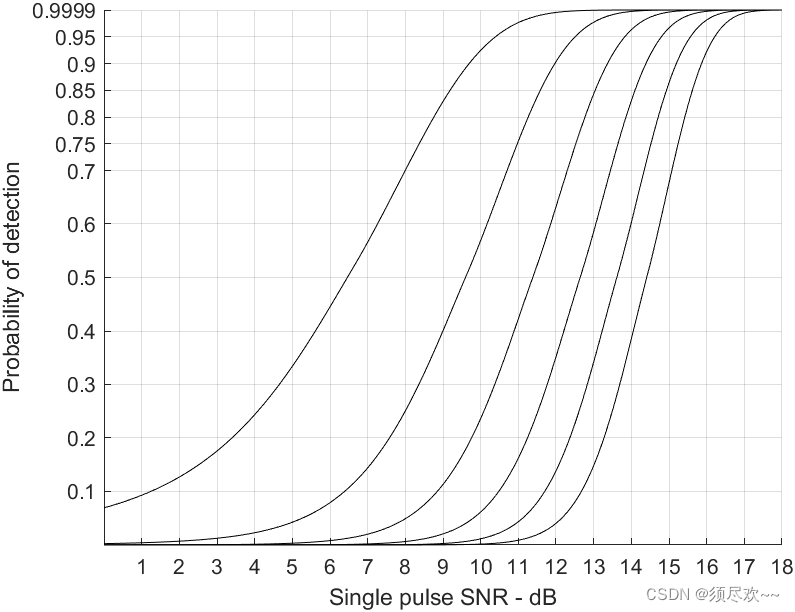
6 кривых

P_{fa}

Слева направо они

10^{-2},10^{-4},10^{-6},10^{-8},10^{-10},10^{-12}

, можно видеть, что по мере увеличения отношения сигнал/шум вероятность обнаружения постепенно увеличивается. Кроме того, чем меньше вероятность ложной тревоги, тем быстрее увеличивается вероятность обнаружения по мере увеличения отношения сигнал/шум.

4. Кривая зависимости коэффициента улучшения и потерь накопления от количества некогерентных импульсов накопления.

I(n_p)

совокупный коэффициент улучшения

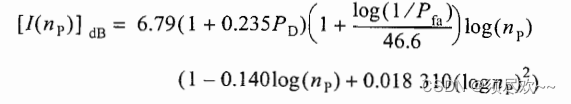
① Кривая зависимости коэффициента улучшения от количества некогерентных накопленных импульсов.
1）MATLAB Исходный код

improv_fac.m

Язык кода:javascript
копировать
function impr_of_np = improv_fac (np, pfa, pd)
% This function computes the non-coherent integration improvment
% factor using the empirical formula defind in Eq. (2.48)
fact1 = 1.0 + log10( 1.0 / pfa) / 46.6;
fact2 = 6.79 * (1.0 + 0.253 * pd);
fact3 = 1.0 - 0.14 * log10(np) + 0.0183 * (log10(np))^2;
impr_of_np = fact1 * fact2 * fact3 * log10(np);
return

fig2_6a.m

Язык кода:javascript
копировать
% This program is used to produce Fig. 2.6a
% It uses the function "improv_fac"
clear all
close all
pfa1 = 1.0e-2;
pfa2 = 1.0e-6;
pfa3 = 1.0e-10;
pfa4 = 1.0e-13;
pd1 = .5;
pd2 = .8;
pd3 = .95;
pd4 = .999;
index = 0;
for np = 1:1:1000
   index = index + 1;
   I1(index) = improv_fac (np, pfa1, pd1);
   I2(index) = improv_fac (np, pfa2, pd2);
   I3(index) = improv_fac (np, pfa3, pd3);
   I4(index) = improv_fac (np, pfa4, pd4);
end
np = 1:1:1000;
semilogx (np, I1, 'k', np, I2, 'k--', np, I3, 'k-.', np, I4, 'k:')
%set (gca,'xtick',[1 2 3 4 5 6 7 8  10 20 30 100]);
xlabel ('Number of pulses');
ylabel ('Improvement factor in dB')
legend ('pd=.5, nfa=e+2','pd=.8, nfa=e+6','pd=.95, nfa=e+10','pd=.999, nfa=e+13');
grid
2) Моделирование

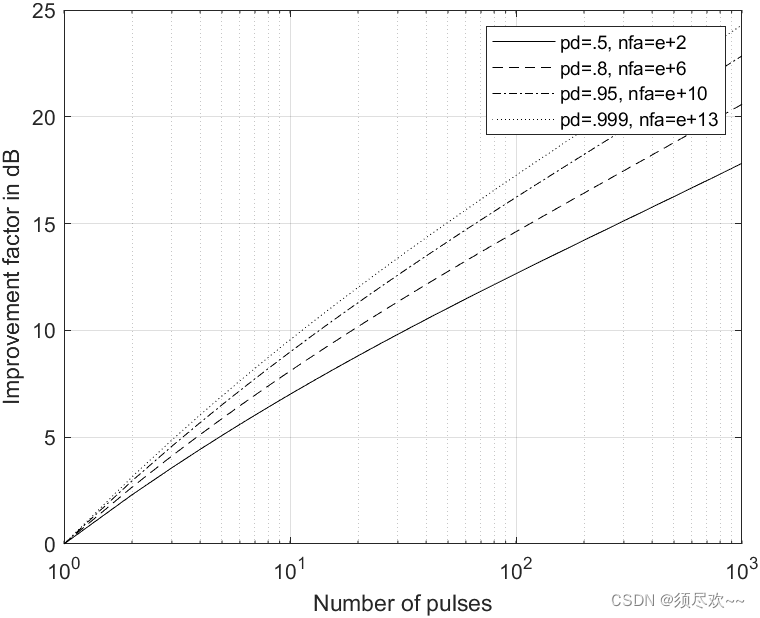
Коэффициент улучшения в зависимости от количества некогерентно накопленных импульсов

Видно, что по мере увеличения количества некогерентных накопленных импульсов коэффициент улучшения постепенно увеличивается при том же количестве импульсов, поскольку вероятность обнаружения и вероятность ложной тревоги также постепенно увеличиваются;

② Кривая зависимости между накопленными потерями и количеством некогерентных накопленных импульсов.
1）MATLAB Исходный код
Язык кода:javascript
копировать
% This program is used to produce Fig. 2.6b
% It uses the function "improv_fac". 
clear all
close all
pfa1 = 1.0e-12;
pfa2 = 1.0e-12;
pfa3 = 1.0e-12;
pfa4 = 1.0e-12;
pd1 = .5;
pd2 = .8;
pd3 = .95;
pd4 = .99;
index = 0;
for np = 1:1:1000
    index = index+1;
    I1 = improv_fac (np, pfa1, pd1);
    i1 = 10.^(0.1*I1);
    L1(index) = -1*10*log10(i1 ./ np);
    I2 = improv_fac (np, pfa2, pd2);
    i2 = 10.^(0.1*I2);
    L2(index) = -1*10*log10(i2 ./ np);
    I3 = improv_fac (np, pfa3, pd3);
    i3 = 10.^(0.1*I3);
    L3(index) = -1*10*log10(i3 ./ np);
    I4 = improv_fac (np, pfa4, pd4);
    i4 = 10.^(0.1*I4);
    L4 (index) = -1*10*log10(i4 ./ np);
end
np = 1:1:1000;
semilogx (np, L1, 'k', np, L2, 'k--', np, L3, 'k-.', np, L4, 'k:')
axis tight
xlabel ('Number of pulses');
ylabel ('Integration loss - dB')
legend ('pd=.5, nfa=e+12','pd=.8, nfa=e+12','pd=.95, nfa=e+12','pd=.99, nfa=e+12');
grid
2) Моделирование

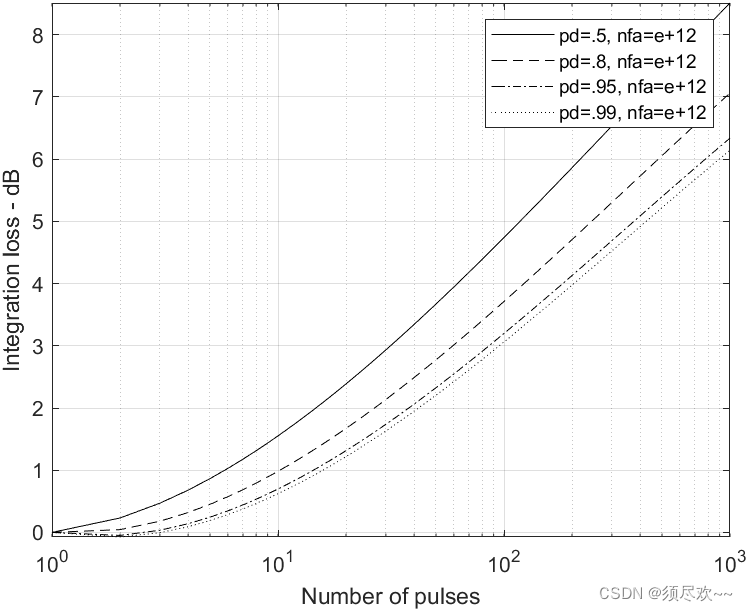
Зависимость потерь накопления от количества некогерентных импульсов накопления

Видно, что по мере увеличения количества некогерентных накопленных импульсов потери накопления постепенно увеличиваются при том же количестве импульсов, по мере увеличения вероятности обнаружения потери накопления будут постепенно уменьшаться;

5. Колеблющаяся вероятность обнаружения цели.

① Обнаружение вертящихся V-образных целей.

вероятность обнаружения

P_D

：

n_p=1,10

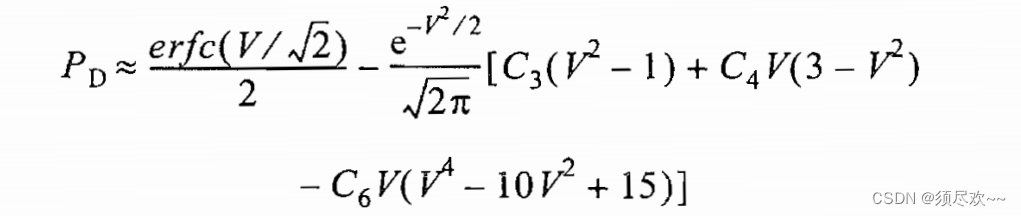
часвероятность обнаруженияотносительно SNR изгиб

1）MATLAB Исходный код

pd_swerling5.m

Язык кода:javascript
копировать
function pd = pd_swerling5 (input1, indicator, np, snrbar)
% This function is used to calculate the probability of detection
% for Swerling 5 or 0 targets for np>1.
if(np == 1)
   'Stop, np must be greater than 1'
   return
end
format long
snrbar = 10.0.^(snrbar./10.);
eps = 0.00000001;
delmax = .00001;
delta =10000.;
% Calculate the threshold Vt
if (indicator ~=1)
   nfa = input1;
   pfa =  np * log(2) / nfa;
else
   pfa = input1;
   nfa = np * log(2) / pfa;
end
sqrtpfa = sqrt(-log10(pfa));
sqrtnp = sqrt(np); 
vt0 = np - sqrtnp + 2.3 * sqrtpfa * (sqrtpfa + sqrtnp - 1.0);
vt = vt0;
while (abs(delta) >= vt0)
   igf = incomplete_gamma(vt0,np);
   num = 0.5^(np/nfa) - igf;
   temp = (np-1) * log(vt0+eps) - vt0 - factor(np-1);
   deno = exp(temp);
   vt = vt0 + (num / (deno+eps));
   delta = abs(vt - vt0) * 10000.0; 
   vt0 = vt;
end
% Calculate the Gram-Chrlier coeffcients
temp1 = 2.0 .* snrbar + 1.0;
omegabar = sqrt(np .* temp1);
c3 = -(snrbar + 1.0 / 3.0) ./ (sqrt(np) .* temp1.^1.5);
c4 = (snrbar + 0.25) ./ (np .* temp1.^2.);
c6 = c3 .* c3 ./2.0;
V = (vt - np .* (1.0 + snrbar)) ./ omegabar;
Vsqr = V .*V;
val1 = exp(-Vsqr ./ 2.0) ./ sqrt( 2.0 * pi);
val2 = c3 .* (V.^2 -1.0) + c4 .* V .* (3.0 - V.^2) -...
   c6 .* V .* (V.^4 - 10. .* V.^2 + 15.0);
q = 0.5 .* erfc (V./sqrt(2.0));
pd =  q - val1 .* val2;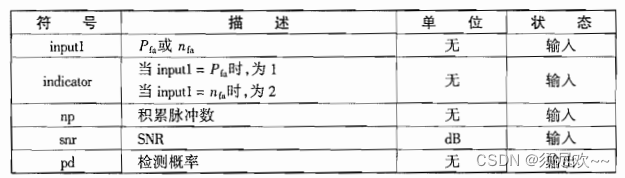

fig2_9.m

Язык кода:javascript
копировать
close all
clear all
pfa = 1e-9;
nfa = log(2) / pfa;
b = sqrt(-2.0 * log(pfa));
index = 0;
for snr = 0:.1:20
   index = index +1;
   a = sqrt(2.0 * 10^(.1*snr));
   pro(index) = marcumsq(a,b);
   prob205(index) =  pd_swerling5 (pfa, 1, 10, snr);
end
x = 0:.1:20;
plot(x, pro,'k',x,prob205,'k:');
axis([0 20 0 1])
xlabel ('SNR - dB')
ylabel ('Probability of detection')
legend('np = 1','np = 10')
grid
2) Моделирование
n_p=1,10

часвероятность обнаруженияотносительно SNR изгиб

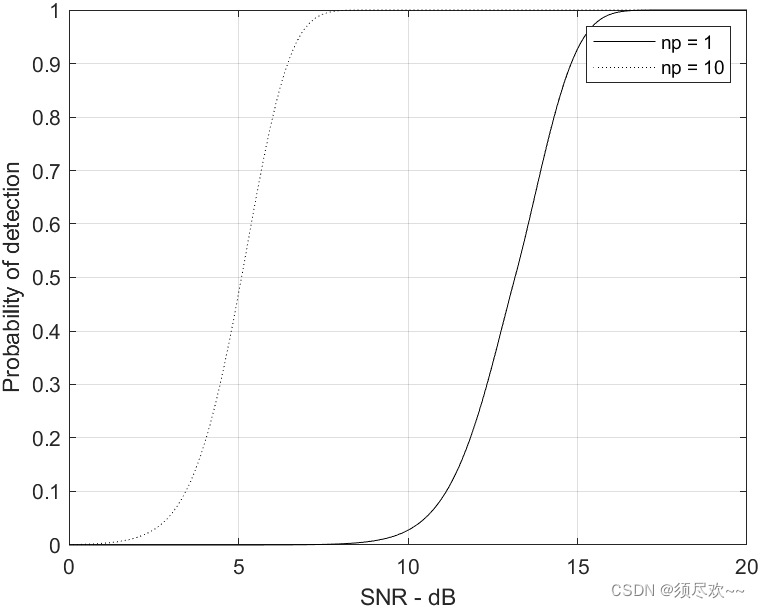
Обратите внимание, что для некогерентного накопления 10 импульсов требуется меньшее отношение сигнал/шум, чем для одного импульса, чтобы получить ту же вероятность обнаружения.

② Обнаружение целей Сверлинга I типа.

вероятность обнаружения

P_D

：

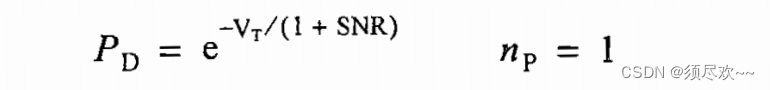
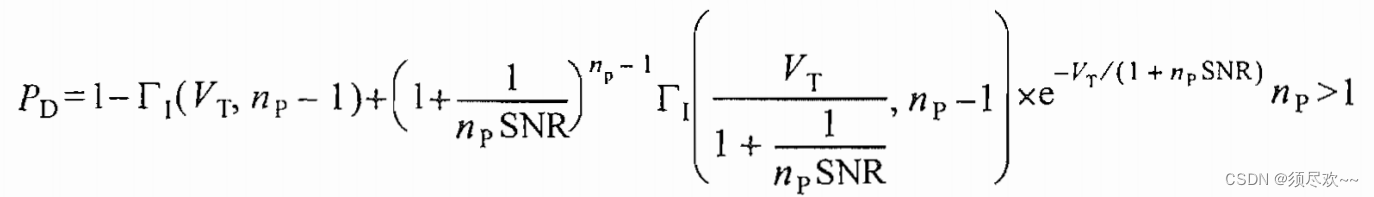
1）MATLAB Исходный код

pd_swerling2.m

Язык кода:javascript
копировать
function pd = pd_swerling2 (nfa, np, snrbar)
% This function is used to calculate the probability of detection
% for Swerling 2 targets.
format long
snrbar = 10.0^(snrbar/10.);
eps = 0.00000001;
delmax = .00001;
delta =10000.;
% Calculate the threshold Vt
pfa =  np * log(2) / nfa;
sqrtpfa = sqrt(-log10(pfa));
sqrtnp = sqrt(np); 
vt0 = np - sqrtnp + 2.3 * sqrtpfa * (sqrtpfa + sqrtnp - 1.0);
vt = vt0;
while (abs(delta) >= vt0)
   igf = incomplete_gamma(vt0,np);
   num = 0.5^(np/nfa) - igf;
   temp = (np-1) * log(vt0+eps) - vt0 - factor(np-1);
   deno = exp(temp);
   vt = vt0 + (num / (deno+eps));
   delta = abs(vt - vt0) * 10000.0; 
   vt0 = vt;
end
if (np <= 50)
   temp = vt / (1.0 + snrbar);
   pd = 1.0 - incomplete_gamma(temp,np);
   return
else
   temp1 = snrbar + 1.0;
   omegabar = sqrt(np) * temp1;
   c3 = -1.0 / sqrt(9.0 * np);
   c4 = 0.25 / np;
   c6 = c3 * c3 /2.0;
   V = (vt - np * temp1) / omegabar;
   Vsqr = V *V;
   val1 = exp(-Vsqr / 2.0) / sqrt( 2.0 * pi);
   val2 = c3 * (V^2 -1.0) + c4 * V * (3.0 - V^2) - ... 
      c6 * V * (V^4 - 10. * V^2 + 15.0);
   q = 0.5 * erfc (V/sqrt(2.0));
   pd =  q - val1 * val2;
end

fig2_10.m

Язык кода:javascript
копировать
clear all
pfa = 1e-9;
nfa = log(2) / pfa;
b = sqrt(-2.0 * log(pfa));
index = 0;
for snr = 0:.01:22
   index = index +1;
   a = sqrt(2.0 * 10^(.1*snr));
   pro(index) = marcumsq(a,b);
   prob(index) =  pd_swerling2 (nfa, 1, snr);
end
x = 0:.01:22;
%figure(10)
plot(x, pro,'k',x,prob,'k:');
axis([2 22 0 1])
xlabel ('SNR - dB')
ylabel ('Probability of detection')
legend('Swerling V','Swerling I')
grid
2) Моделирование

вероятность обнаруженияотносительно SNR, одиночный импульс,

P_{fa}=10^{-9}

：

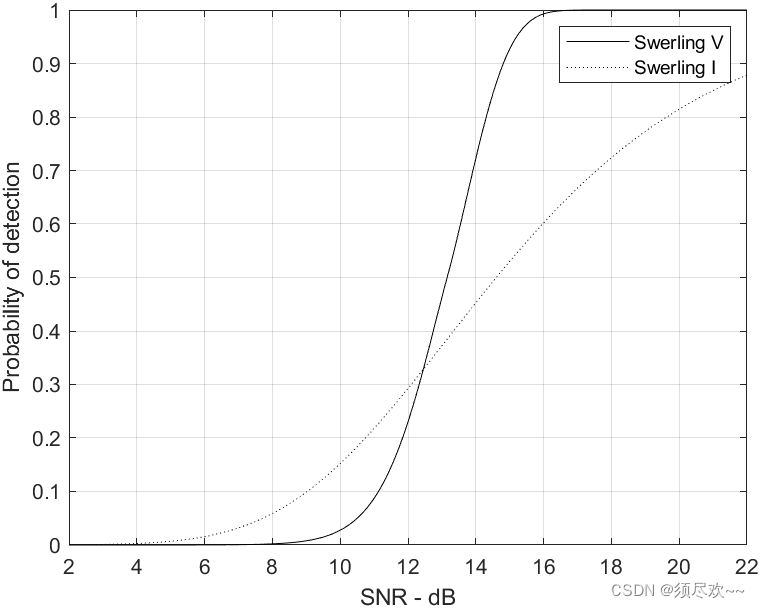
Видно, что для того, чтобы получить то же, что и в безфлуктуационном случае

P_D

, когда есть взлеты и падения, требуется более высокий SNR.

3）MATLAB Исходный код

pd_swerling1.m

Язык кода:javascript
копировать
function pd = pd_swerling1 (nfa, np, snrbar)
% This function is used to calculate the probability of detection
% for Swerling 1 targets.
format long
snrbar = 10.0^(snrbar/10.);
eps = 0.00000001;
delmax = .00001;
delta =10000.;
% Calculate the threshold Vt
pfa =  np * log(2) / nfa;
sqrtpfa = sqrt(-log10(pfa));
sqrtnp = sqrt(np); 
vt0 = np - sqrtnp + 2.3 * sqrtpfa * (sqrtpfa + sqrtnp - 1.0);
vt = vt0;
while (abs(delta) >= vt0)
   igf = incomplete_gamma(vt0,np);
   num = 0.5^(np/nfa) - igf;
   temp = (np-1) * log(vt0+eps) - vt0 - factor(np-1);
   deno = exp(temp);
   vt = vt0 + (num / (deno+eps));
   delta = abs(vt - vt0) * 10000.0; 
   vt0 = vt;
end
if (np == 1)
   temp = -vt / (1.0 + snrbar);
   pd = exp(temp);
   return
end
   temp1 = 1.0 + np * snrbar;
   temp2 = 1.0 / (np *snrbar);
   temp = 1.0 + temp2;
   val1 = temp^(np-1.);
   igf1 = incomplete_gamma(vt,np-1);
   igf2 = incomplete_gamma(vt/temp,np-1);
   pd = 1.0 - igf1 + val1 * igf2 * exp(-vt/temp1);

fig2_11ab.m

Язык кода:javascript
копировать
clear all
pfa = 1e-11;
nfa = log(2) / pfa;
index = 0;
for snr = -10:.5:30
   index = index +1;
   prob1(index) =  pd_swerling1 (nfa, 1, snr);
   prob10(index) =  pd_swerling1 (nfa, 10, snr);
   prob50(index) =  pd_swerling1 (nfa, 50, snr);
   prob100(index) =  pd_swerling1 (nfa, 100, snr);
end
x = -10:.5:30;
plot(x, prob1,'k',x,prob10,'k:',x,prob50,'k--', ...
   x, prob100,'k-.');
axis([-10 30 0 1])
xlabel ('SNR - dB')
ylabel ('Probability of detection')
legend('np = 1','np = 10','np = 50','np = 100')
grid
4) Моделирование

вероятность обнаруженияотносительно SNR,Swerling Ⅰ,

P_{fa}=10^{-8}

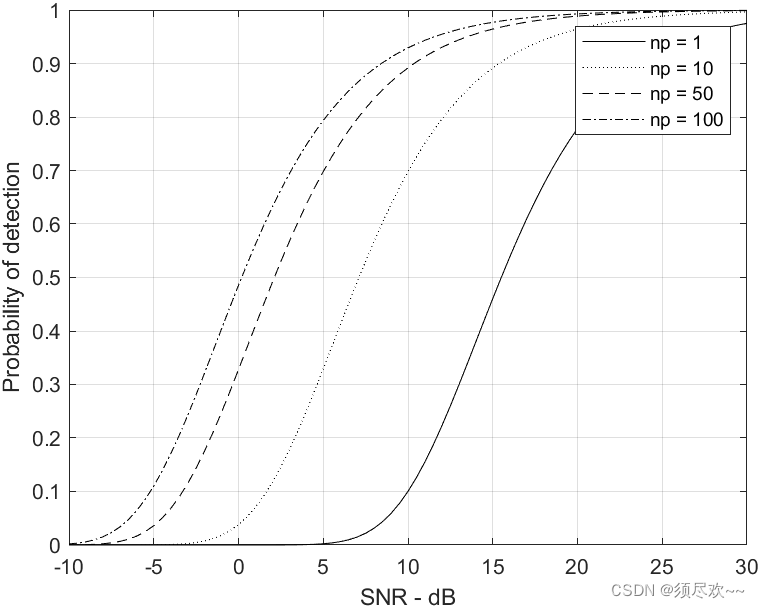
На картинке выше показано

n_p=1,10,50,100

час,вероятность обнаруженияотносительно SNR изгибы, среди которых

P_{fa}=10^{-8}

, ты можешь видеть

n_p

Чем больше, тем достигаются одни и те же возможности обнаруженияиз SNR Чем меньше.

③ Обнаружение целей Сверлинга II типа.

вероятность обнаружения

P_D

：

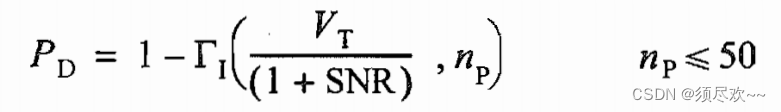
когда

n_p > 50

час:

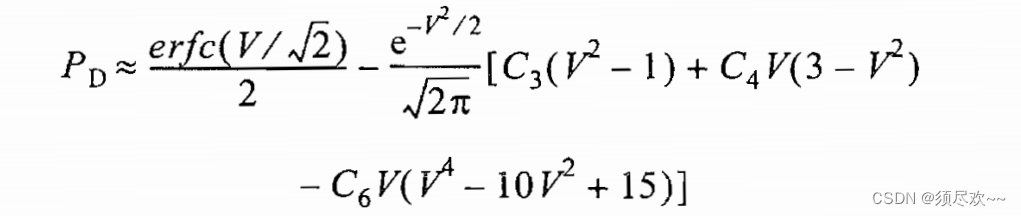
в это время:

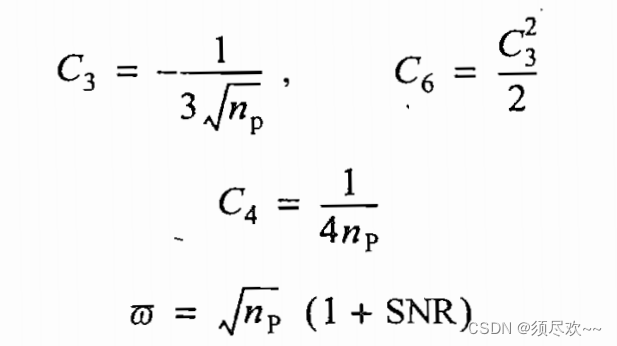
1）MATLAB Исходный код

fig2_12.m

Язык кода:javascript
копировать
clear all
pfa = 1e-10;
nfa = log(2) / pfa;
index = 0;
for snr = -10:.5:30
   index = index +1;
   prob1(index) =  pd_swerling2 (nfa, 1, snr);
   prob10(index) =  pd_swerling2 (nfa, 10, snr);
   prob50(index) =  pd_swerling2 (nfa, 50, snr);
   prob100(index) =  pd_swerling2 (nfa, 100, snr);
end
x = -10:.5:30;
plot(x, prob1,'k',x,prob10,'k:',x,prob50,'k--', ...
   x, prob100,'k-.');
axis([-10 30 0 1])
xlabel ('SNR - dB')
ylabel ('Probability of detection')
legend('np = 1','np = 10','np = 50','np = 100')
grid
2) Моделирование

вероятность обнаруженияотносительно SNR,Swerling Ⅱ,

P_{fa}=10^{-10}

На картинке выше показано, когда

n_p=1,10,50,100

час,вероятность обнаружениякак SNR функцияизгибы, среди которых

P_{fa}=10^{-10}
④ Обнаружение целей Сверлинга III типа.

вероятность обнаружения

P_D

：

n_p=1,2

час:

n_p>2

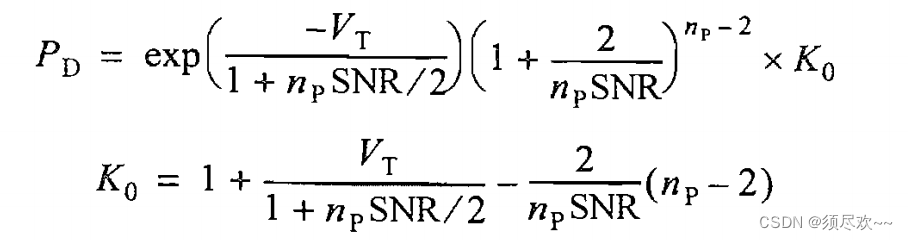
час:

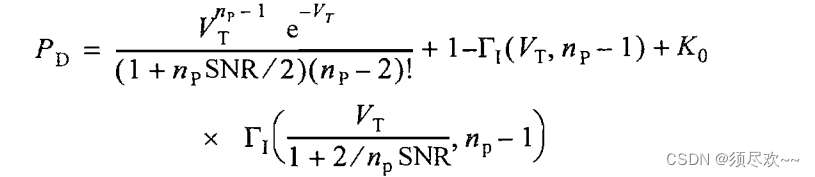
1）MATLAB Исходный код

pd_swerling3.m

Язык кода:javascript
копировать
function pd = pd_swerling3 (nfa, np, snrbar)
% This function is used to calculate the probability of detection
% for Swerling 2 targets.
format long
snrbar = 10.0^(snrbar/10.);
eps = 0.00000001;
delmax = .00001;
delta =10000.;
% Calculate the threshold Vt
pfa =  np * log(2) / nfa;
sqrtpfa = sqrt(-log10(pfa));
sqrtnp = sqrt(np); 
vt0 = np - sqrtnp + 2.3 * sqrtpfa * (sqrtpfa + sqrtnp - 1.0);
vt = vt0;
while (abs(delta) >= vt0)
   igf = incomplete_gamma(vt0,np);
   num = 0.5^(np/nfa) - igf;
   temp = (np-1) * log(vt0+eps) - vt0 - factor(np-1);
   deno = exp(temp);
   vt = vt0 + (num / (deno+eps));
   delta = abs(vt - vt0) * 10000.0; 
   vt0 = vt;
end
temp1 = vt / (1.0 + 0.5 * np *snrbar);
temp2 = 1.0 + 2.0 / (np * snrbar);
temp3 = 2.0 * (np - 2.0) / (np * snrbar);
ko = exp(-temp1) * temp2^(np-2.) * (1.0 + temp1 - temp3);
if (np <= 2)
   pd = ko;
   return
else
   temp4 = vt^(np-1.) * exp(-vt) / (temp1 * exp(factor(np-2.)));
   temp5 =  vt / (1.0 + 2.0 / (np *snrbar));
   pd = temp4 + 1.0 - incomplete_gamma(vt,np-1.) + ko * ...
      incomplete_gamma(temp5,np-1.);
end

fig2_13.m

Язык кода:javascript
копировать
clear all
pfa = 1e-9;
nfa = log(2) / pfa;
index = 0;
for snr = -10:.5:30
   index = index +1;
   prob1(index) =  pd_swerling3 (nfa, 1, snr);
   prob10(index) =  pd_swerling3 (nfa, 10, snr);
   prob50(index) =  pd_swerling3(nfa, 50, snr);
   prob100(index) =  pd_swerling3 (nfa, 100, snr);
end
x = -10:.5:30;
plot(x, prob1,'k',x,prob10,'k:',x,prob50,'k--', ...
   x, prob100,'k-.');
axis([-10 30 0 1])
xlabel ('SNR - dB')
ylabel ('Probability of detection')
legend('np = 1','np = 10','np = 50','np = 100')
grid
2) Моделирование

вероятность обнаруженияотносительно SNR,Swerling Ⅲ,

P_{fa}=10^{-9}

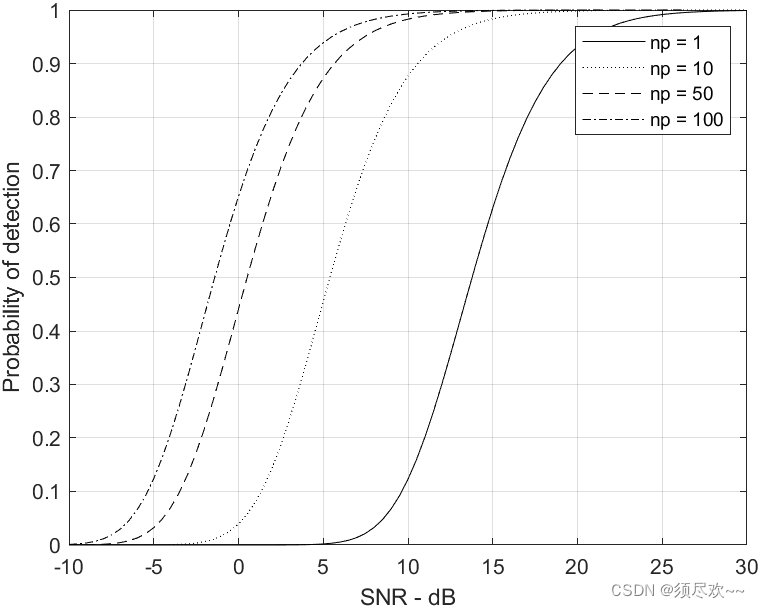
На картинке выше показано, когда

n_p=1,10,50,100

час,вероятность обнаружениякак SNR функцияизгибы, среди которых

P_{fa}=10^{-9}
⑤ Обнаружение целей Сверлинга типа IV.

вероятность обнаружения

P_D

：

n_p <50

час:

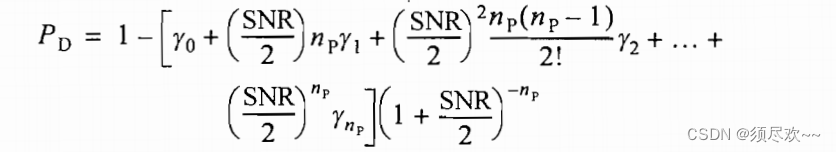
когда

n_p > 50

час:

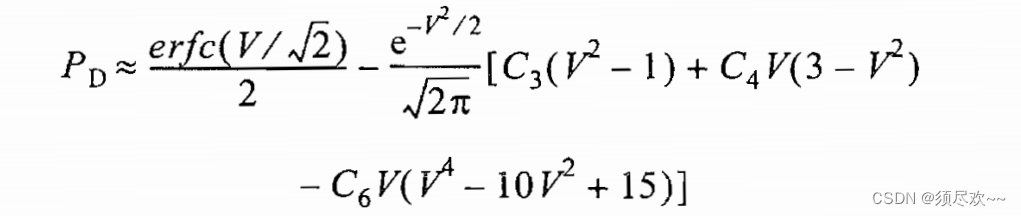
в это время:

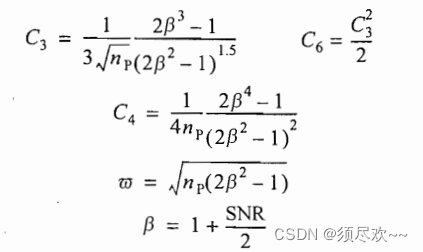
1）MATLAB Исходный код

pd_swerling4.m

Язык кода:javascript
копировать
function pd = pd_swerling4 (nfa, np, snrbar)
% This function is used to calculate the probability of detection
% for Swerling 4 targets.
format long
snrbar = 10.0^(snrbar/10.);
eps = 0.00000001;
delmax = .00001;
delta =10000.;
% Calculate the threshold Vt
pfa =  np * log(2) / nfa;
sqrtpfa = sqrt(-log10(pfa));
sqrtnp = sqrt(np); 
vt0 = np - sqrtnp + 2.3 * sqrtpfa * (sqrtpfa + sqrtnp - 1.0);
vt = vt0;
while (abs(delta) >= vt0)
   igf = incomplete_gamma(vt0,np);
   num = 0.5^(np/nfa) - igf;
   temp = (np-1) * log(vt0+eps) - vt0 - factor(np-1);
   deno = exp(temp);
   vt = vt0 + (num / (deno+eps));
   delta = abs(vt - vt0) * 10000.0; 
   vt0 = vt;
end
h8 = snrbar /2.0;
beta = 1.0 + h8;
beta2 = 2.0 * beta^2 - 1.0;
beta3 = 2.0 * beta^3;
if (np >= 50)
   temp1 = 2.0 * beta -1;
   omegabar = sqrt(np * temp1);
   c3 = (beta3 - 1.) / 3.0 / beta2 / omegabar;
   c4 = (beta3 * beta3 - 1.0) / 4. / np /beta2 /beta2;;
   c6 = c3 * c3 /2.0;
   V = (vt - np * (1.0 + snrbar)) / omegabar;
   Vsqr = V *V;
   val1 = exp(-Vsqr / 2.0) / sqrt( 2.0 * pi);
   val2 = c3 * (V^2 -1.0) + c4 * V * (3.0 - V^2) - ... 
      c6 * V * (V^4 - 10. * V^2 + 15.0);
   q = 0.5 * erfc (V/sqrt(2.0));
   pd =  q - val1 * val2;
   return
else
   snr = 1.0;
   gamma0 = incomplete_gamma(vt/beta,np);
   a1 = (vt / beta)^np / (exp(factor(np)) * exp(vt/beta));
   sum = gamma0;
   for i = 1:1:np
      temp1 = 1;
      if (i == 1)
         ai = a1;
      else
         ai = (vt / beta) * a1 / (np + i -1);
      end
      a1 = ai;
      gammai = gamma0 - ai;
      gamma0 = gammai;
      a1 = ai;

      for ii = 1:1:i
         temp1 = temp1 * (np + 1 - ii);
      end
      term = (snrbar /2.0)^i * gammai * temp1 / exp(factor(i));
      sum = sum + term;
   end
   pd = 1.0 - sum / beta^np;
end
pd = max(pd,0.);

fig2_14.m

Язык кода:javascript
копировать
clear all
pfa = 1e-9;
nfa = log(2) / pfa;
index = 0;
for snr = -10:.5:30
   index = index +1;
   prob1(index) =  pd_swerling4 (nfa, 1, snr);
   prob10(index) =  pd_swerling4 (nfa, 10, snr);
   prob50(index) =  pd_swerling4(nfa, 50, snr);
   prob100(index) =  pd_swerling4 (nfa, 100, snr);
end
x = -10:.5:30;
plot(x, prob1,'k',x,prob10,'k:',x,prob50,'k--', ...
   x, prob100,'k-.');
axis([-10 30 0 1.1])
xlabel ('SNR - dB')
ylabel ('Probability of detection')
legend('np = 1','np = 10','np = 50','np = 100')
grid
axis tight
2) Моделирование

вероятность обнаруженияотносительно SNR,Swerling Ⅳ,

P_{fa}=10^{-9}

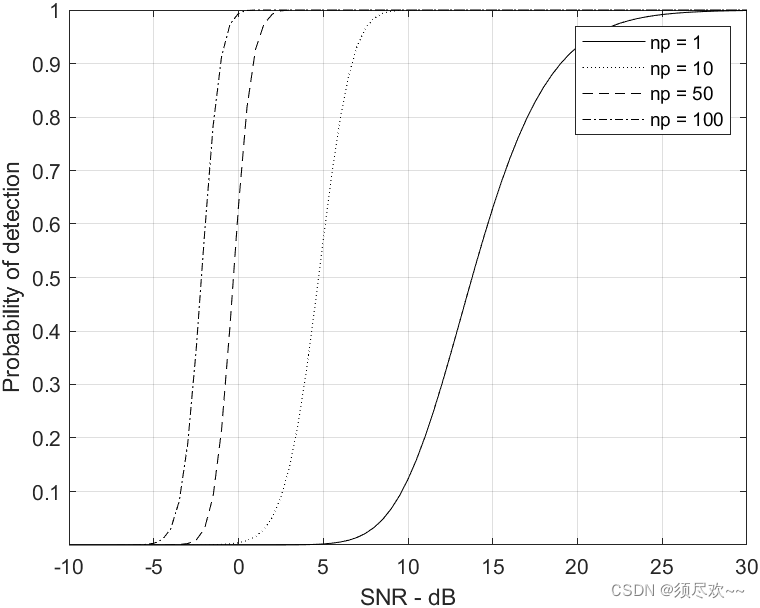
На картинке выше показано, когда

n_p=1,10,50,100

час,вероятность обнаружениякак SNR функцияизгибы, среди которых

P_{fa}=10^{-9}

boy illustration
Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.
boy illustration
Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).
boy illustration
Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)
boy illustration
Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.
boy illustration
Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
boy illustration
Идеальная интеграция Cursor и DeepSeek API
boy illustration
DeepSeek V3 снижает затраты на обучение больших моделей
boy illustration
Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).
boy illustration
DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».
boy illustration
Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.
boy illustration
Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле
boy illustration
Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.
boy illustration
9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать
boy illustration
Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.
boy illustration
Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)
boy illustration
50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.
boy illustration
Cloud Native｜Практика: установка Dashbaord для K8s, графика неплохая
boy illustration
Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности
boy illustration
MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.
boy illustration
Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.
boy illustration
Центр конфигурации————Накос
boy illustration
Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще
boy illustration
[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64
boy illustration
Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике
boy illustration
Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах
boy illustration
Feiniu fnos использует Docker для развертывания личного блокнота Notepad
boy illustration
Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch
boy illustration
Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов
boy illustration
[Зона легкого облачного игрового сервера] Управление игровыми архивами
boy illustration
Развертывание SpringCloud-проекта на базе Docker и Docker-Compose
©