Python реализует линейную интерполяцию, параболическую интерполяцию, сплайн-интерполяцию, лагранжеву интерполяцию, интерполяцию Ньютона и интерполяцию Эмильтера.
Публичный аккаунт: Youerhut Редактор: Питер Автор: Питер
Привет всем, я Питер~
Позвольте мне представить вам сегодня7метод интерполяции:Линейная интерполяция, параболическая интерполяция、полиномиальная интерполяция、сплайн-интерполяция、Лагранжева интерполяция、Интерполяция Ньютона、Интерполяция Эрмита,И предоставить примеры реализации Python.
Импортировать библиотеку
Импортируйте библиотеки, необходимые для обработки и моделирования данных:
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif'] = ['SimHei'] # Показать китайскую этикетку
plt.rcParams['axes.unicode_minus'] = False # Показать отрицательный знак
import warnings
warnings.filterwarnings("ignore")Линейная интерполяция interp1d
Линейная интерполяция — это математический метод, используемый для оценки неизвестного значения между двумя известными значениями.。Этот метод предполагает, что изменение между этими двумя известными точками линейно.,То есть скорость изменения постоянна. Линейная интерполяция проста и интуитивно понятна,Во многих областях, таких как обработка изображений, анализ данные и т. д. широко используются.
В частности, принцип линейной интерполяции можно описать так:
- Определить известные точки:Должно быть два известныхточки данных,Обычно выражается как (x0, y0) и (x1, y1).
- Вычислить коэффициенты интерполяции:Этот коэффициент определяется как $α = (x - x_0) / (x_1 - x_0)$, где x — местоположение оцениваемой стоимости.
- Примените формулу линейной интерполяции:По коэффициенту интерполяции α, можно использовать формулу $y = (1 - α)y_0 + αy_1$ рассчитать y ценить. Эта формула объясняет y Значение определяется выражением y0 и y1 По их расстоянию x Получено средневзвешенным относительным положением.
- Расширьтесь в многомерное пространство:линейная интерполяция Может быть расширен до двух или трех измерений.,Они называются билинейной интерполяцией и трилинейной интерполяцией соответственно. в двумерном пространстве,Сначала выполните две линейные интерполяции вдоль одной оси.,Затем выполните линейную интерполяцию по другой оси,Таким образом, получается окончательный результат интерполяции.
В практических приложениях линейная интерполяция часто используется для оценки значений пикселей при изменении размера изображения, разумной компенсации при отсутствии данных и масштабирования данных.
из-за своей простоты,Линейная интерполяция имеет высокую вычислительную эффективность.,Легко реализовать. Однако,Он основан на предположении о линейном изменении,Для данных с нелинейными связями,Линейная интерполяция может не дать наиболее точной оценки. в этих случаях,Возможно, потребуется использовать методы интерполяции более высокого порядка.,нравитьсяполиномиальная интерполяцияилисплайн-интерполяцияждать。
from scipy.interpolate import interp1d
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 3, 4, 1, 0, 4])
# Создайте функцию линейной интерполяции
f = interp1d(x, y, kind='linear')
# Рассчитать результаты интерполяции
x_new = np.linspace(0, 5, 100)
y_new = f(x_new)
# Нарисуйте график xуy
plt.plot(x, y, 'o', label='исходные данные')
# Нарисуйте график x_newиy_new
plt.plot(x_new, y_new, '-', label='результат линейной интерполяции')
# Добавить легенду
plt.legend()
# отображать графику
plt.show()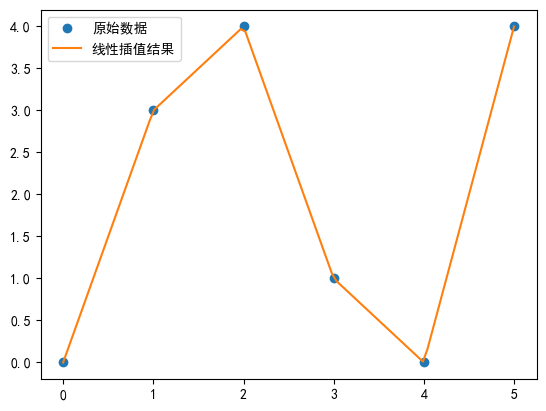
параболическая интерполяция
параболическая интерполяция,Также известна как квадратичная интерполяция,это своего рода полиномиальная метод интерполяции. Этот метод использует известные точки данные для построения квадратичного полинома,Используйте это как приближение к неизвестной функции.
import numpy as np
import matplotlib.pyplot as plt
# точки данных
x = np.array([0, 1, 2, 3])
y = np.array([0, 0.8, 0.9, 0.1])
# Используйте функцию Polyfit numpy для квадратичной подгонки (т.е. параболической интерполяция), возвращает коэффициенты аппроксимирующего полинома
# От высшей степени к низшей, например для ax^2 + bx + c, возвращает [a, b, c]
coeffs = np.polyfit(x, y, 2)
# Тестовые данные: x_min и x_max Наберите 100 очков между
x_new = np.linspace(min(x), max(x), 100) # Сгенерировать более детальный массив значений x для интерполяции
y_new = np.polyval(coeffs, x_new) # Результаты подгонки
# нарисовать исходные точки кривая интерполяции данных
plt.scatter(x, y, label='Data points', color='red')
plt.plot(x_new, y_new, label='Parabolic Interpolation', color='blue')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()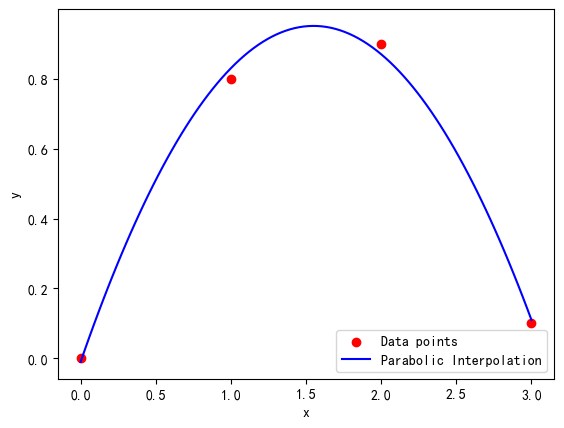
Полиномиальная интерполяция
from scipy.interpolate import BarycentricInterpolator
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 3, 4, 1, 0, 4])
# Создайте функцию полиномиальной интерполяции
f = BarycentricInterpolator(x, y)
# Рассчитать результаты интерполяции
x_new = np.linspace(0, 5, 100)
y_new = f(x_new)
# Нарисуйте график xуy
plt.plot(x, y, 'o', label='исходные данные')
# Нарисуйте график x_newиy_new
plt.plot(x_new, y_new, '-', label='Результат полиномиальной интерполяции')
# Добавить легенду
plt.legend()
# отображать графику
plt.show()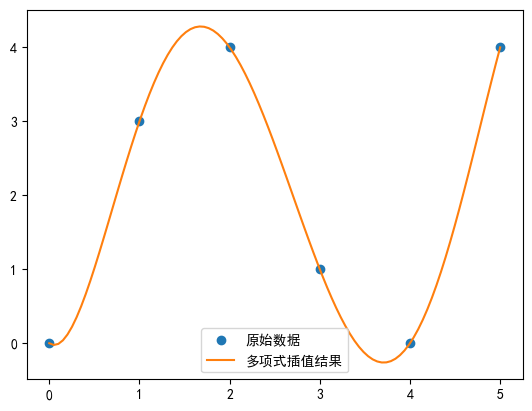
сплайн-интерполяция
сплайн-интерполяция — метод численного анализа.,используется для передачи заданного набораточки данныхПостроить плавную кривую。Его основная идея состоит в том, чтобыточки данныхпостроен междуполиномиальная функция,Эти функции соседствуют сточки данных Иметь везденепрерывная первая производная,Это создает плавную кривую.
На основе CubicSpline
from scipy.interpolate import CubicSpline # 3Второсортныйсплайн-интерполяцияCubicSpline
# Пример данных
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 3, 4, 1, 0, 4])
# Создайте трижды функцию сплайн-интерполяции
cs = CubicSpline(x, y)
# Рассчитать результаты интерполяции
x_new = np.linspace(0, 5, 100)
y_new = cs(x_new)
# Нарисуйте график xуy
plt.plot(x, y, 'o', label='исходные данные')
# Нарисуйте график x_newиy_new
plt.plot(x_new, y_new, '-', label='сплайн-интерполяциярезультат')
# Добавить легенду
plt.legend()
# отображать графику
plt.show()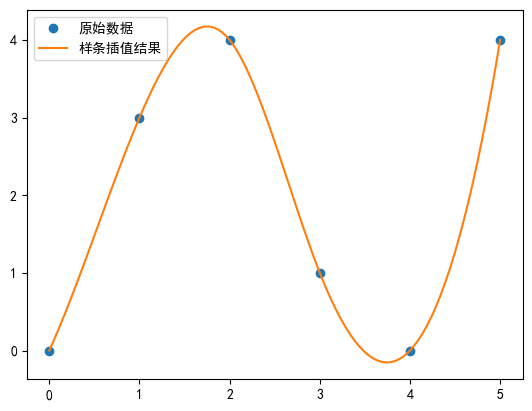
На основе interp1d(kind='cubic')
from scipy.interpolate import interp1d
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 3, 4, 1, 0, 4])
# Создайте функцию линейной интерполяции
f = interp1d(x, y, kind='cubic') # Указано как кубическое: 3 раза
# Рассчитать результаты интерполяции
x_new = np.linspace(0, 5, 100)
y_new = f(x_new)
# Нарисуйте график xуy
plt.plot(x, y, 'o', label='исходные данные')
# Нарисуйте график x_newиy_new
plt.plot(x_new, y_new, '-', label='сплайн-интерполяциярезультат')
# Добавить легенду
plt.legend()
# отображать графику
plt.show()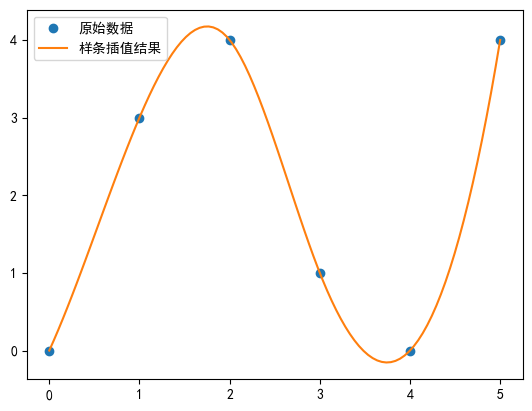
Метод интерполяции Лагранжа Лагранж
Лагранжева интерполяция также является разновидностью полиномиальной интерполяции. Ее принцип заключается в построении полинома высокого порядка $p через несколько точек выборки $(x_i,y_i)(i=0,1,2,3...,n)$ (. x)$, чтобы примерно заменить $f(x)$
from scipy.interpolate import lagrange
# Пример данных
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 3, 4, 1, 0, 4])
# Создайте функцию интерполяции Лагранжа
f = lagrange(x, y)
# Рассчитать результаты интерполяции
x_new = np.linspace(0, 5, 100)
y_new = f(x_new)
# Нарисуйте график xуy
plt.plot(x, y, 'o', label='исходные данные')
# Нарисуйте график x_newиy_new
plt.plot(x_new, y_new, '-', label='Результат интерполяции Лагранжа')
# Добавить легенду
plt.legend()
# отображать графику
plt.show()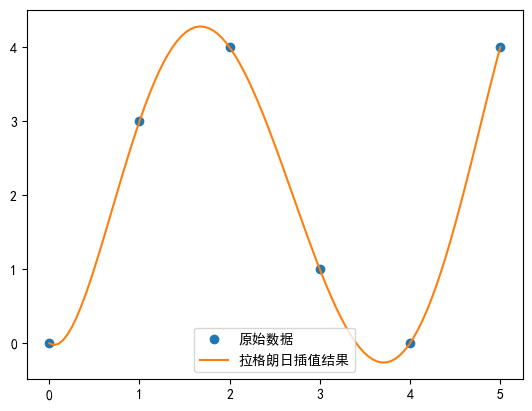
Метод интерполяции Ньютона Ньютон
Интерполяция Ньютона Основная идея заключается в использованииразницаиПлохой бизнесконцепция построения интерполяционных полиномов。Плохой бизнесэто своего родаоперация специального подразделения,Используется для расчета разницы между значениями функции.,Разница представляет собой дискретную форму коэффициента разности.
Интерполяция Ньютона多项式的структурарассчитывается путем вычисления нулевого порядкаnзаказ Плохой бизнес, которого нужно достичь. Эти Плохой бизнес Может использоваться для постепенного построения интерполирующих полиномов.,Добавляйте по одному элементу за раз,пока не будет достигнуто необходимое количество раз
import numpy as np
def newton_interpolation(x, y):
"""
Интерполяция Ньютона
x: Список абсцисс известных точек
y: Список ординат известных точек
return: интерполирующая полиномиальная функция
"""
n = len(x)
# Инициализировать таблицу коэффициентов разницы
f = [[0] * n for _ in range(n)] # n*n весь 0-мерный массив
for i in range(n):
f[i][0] = y[i] # Присвойте ординату известной точки первому столбцу таблицы разностных коэффициентов.
for j in range(1, n): # j представляет собой порядок разностного коэффициента
for i in range(n - j): # я используется для перебора начальной позиции каждой строки
f[i][j] = (f[i + 1][j - 1] - f[i][j - 1]) / (x[i + j] - x[i]) # Вычислить коэффициент разницы
# структураинтерполирующая полиномиальная функция
def P(t):
result = 0 # начальное значение
for i in range(n): # двойная петля
temp = 1 # Временная переменная, используемая для вычисления произведения (t-x[j])
for j in range(i):
temp *= (t - x[j])
result += f[0][i] * temp # Накопите произведение разностного коэффициента и (t-x[j]) в результат
return result
return P # Пример данных
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 3, 4, 1, 0, 4])
P = newton_interpolation(x,y)
# Рассчитать результаты интерполяции
x_new = np.linspace(0, 5, 100)
y_new = P(x_new)# Нарисуйте график xуy
plt.plot(x, y, 'o', label='исходные данные')
# Нарисуйте график x_newиy_new
plt.plot(x_new, y_new, '-', label='Результат интерполяции Ньютона')
# Добавить легенду
plt.legend()
# отображать графику
plt.show()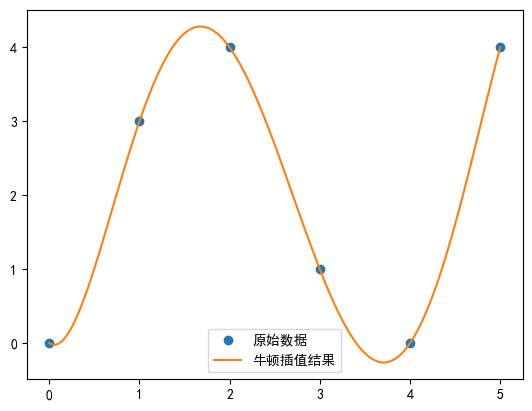
Метод интерполяции Эрмита Эрмит
Эрмитова интерполяция — это еще один тип задачи интерполяции. Этот тип интерполяции требует, чтобы значение функции интерполяционного полинома было таким же, как исходное значение функции в данном узле.
При этом также требуется, чтобы в узле значение производной первого порядка до заданного порядка интерполяционного полинома также было равно соответствующему значению производной порядка интерполируемой функции.,Такая интерполяция называется интерполяцией Эрмита.
import numpy as np
from scipy.interpolate import CubicHermiteSpline
# Пример данных
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 3, 4, 1, 0, 4])
dy = np.array([3, 1, -3, -1, 4,0])
# Создайте функцию интерполяции Эрмита
f = CubicHermiteSpline(x, y, dy)
# Рассчитать результаты интерполяции
x_new = np.linspace(0, 5, 100)
y_new = f(x_new)
# Нарисуйте график xуy
plt.plot(x, y, 'o', label='исходные данные')
# Нарисуйте график x_newиy_new
plt.plot(x_new, y_new, '-', label='Результат интерполяции Эрмита')
# Добавить легенду
plt.legend()
# отображать графику
plt.show()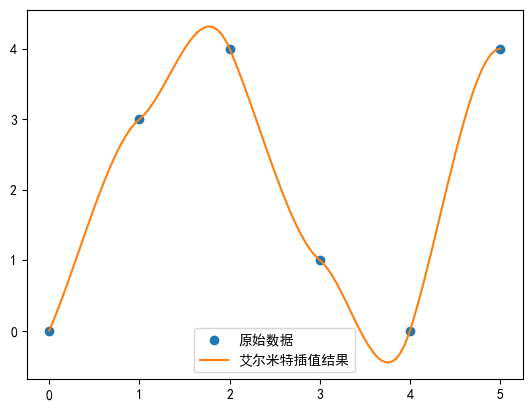

Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.

Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).

Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)

Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.

Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
Идеальная интеграция Cursor и DeepSeek API

DeepSeek V3 снижает затраты на обучение больших моделей

Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).

DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».

Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.

Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле

Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.

9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать

Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.

Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)

50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.

Cloud Native|Практика: установка Dashbaord для K8s, графика неплохая

Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности

MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.

Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.

Центр конфигурации————Накос

Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще

[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64

Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике

Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах

Feiniu fnos использует Docker для развертывания личного блокнота Notepad

Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов

[Зона легкого облачного игрового сервера] Управление игровыми архивами


