1. Введение

1.1 Обзор модели линейной регрессии

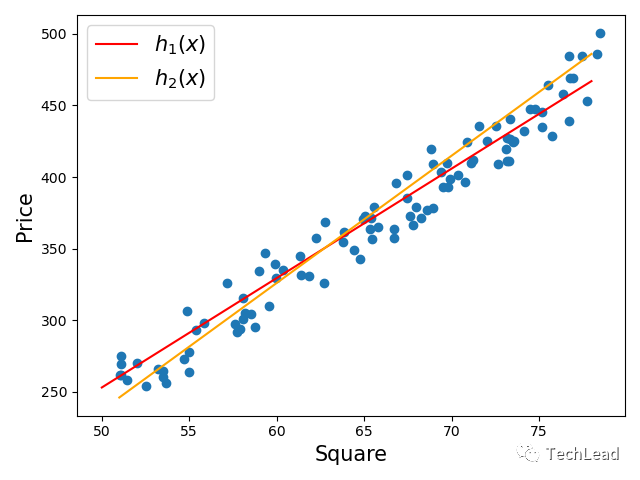
линейная регрессиястатистическийизПрогнозная аналитика,Этот метод используется для установления связи между двумя или более переменными. линейная регрессия использует наиболее подходящую прямую линию (также называемую линией регрессии) для установления интуитивной взаимосвязи между независимой (входной) переменной и зависимой переменной (выходной). Простая линейная регрессия – это линейная связь между входными и выходными переменными, а многомерная линейная регрессия — это линейная зависимость между несколькими входными и выходными переменными.

1.2 Введение в Python и PyTorch

Python — мощный язык программирования, который особенно подходит для обработки и анализа больших данных и широко используется в различных научных расчетах. Python имеет множество библиотек, которые могут легко реализовать различные расширенные функции, такие как: NumPy, Pandas, Matplotlib и т. д.

PyTorch — это библиотека машинного обучения Python с открытым исходным кодом, основанная на Torch. В первую очередь он был разработан исследовательской группой Facebook по искусственному интеллекту для реализации алгоритмов глубокого обучения. PyTorch использует тензоры в качестве базовой структуры данных и может выполнять вычисления на графическом процессоре или процессоре. Возможность динамического определения вычислительных графов делает PyTorch более выгодным при написании и отладке моделей.

В следующем разделе мы реализуем модель линейной регрессии с использованием Python и библиотеки PyTorch.

2. Подготовка инструментов и библиотек

Прежде чем приступить к реализации модели линейной регрессии, нам необходимо подготовить соответствующие инструменты и библиотеки. Мы будем использовать Python в качестве языка программирования и PyTorch в качестве основной библиотеки глубокого обучения.

2.1 Конфигурация среды Python

Сначала нам нужно установить Python. Если Python не установлен на вашем компьютере, вы можете загрузить его с официального сайта Python: https://www.python.org/downloads/. После завершения установки вы можете проверить, успешно ли установлен Python, выполнив следующую команду: команда в командной строке:

python --version

Вы должны увидеть номер версии Python. Если Python был успешно установлен, мы можем начать установку необходимых библиотек Python. Эти библиотеки включают: NumPy, Pandas, Matplotlib и PyTorch.

2.2 Введение в установку и использование PyTorch

Далее нам нужно установить библиотеку PyTorch. Процесс установки PyTorch зависит от вашей операционной системы и от того, установлен ли у вас CUDA (если вы планируете запускать PyTorch на графическом процессоре, вам понадобится CUDA). Подробное руководство по установке можно найти на официальном сайте PyTorch: https://pytorch.org/get-started/locally/.

Выполните следующие команды в командной строке, выбрав соответствующую команду в зависимости от вашей среды:

# For CPU only
pip install torch==1.9.0+cpu torchvision==0.10.0+cpu torchaudio===0.9.0 -f https://download.pytorch.org/whl/torch_stable.html

# For CUDA 10.2
pip install torch==1.9.0+cu102 torchvision==0.10.0+cu102 torchaudio===0.9.0 -f https://download.pytorch.org/whl/torch_stable.html

После завершения установки мы можем убедиться, что PyTorch был успешно установлен, выполнив следующий код Python:

import torch
print(torch.__version__)

3. Подготовка данных

3.1 Обзор набора данных

В этом примере мы будем использовать вымышленный набор данных, содержащий информацию о размере и цене дома. Наша цель — спрогнозировать цены на жилье по районам, что является типичной задачей линейной регрессии.

Предположим, у нас есть следующие данные:

3.2 Загрузка и предварительная обработка данных

Далее нам нужно загрузить данные и предварительно их обработать. Обычно это включает в себя такие шаги, как обработка пропущенных значений, нормализация данных и т. д. В этом примере мы предполагаем, что все данные полны и обработка пропущенных значений не требуется. Однако для того, чтобы алгоритм градиентного спуска сходился быстрее, нам необходимо нормализовать данные.

import numpy as np

# Площадь дома
areas = np.array([50, 60, 70, ..., 120, 130, 140], dtype=float)

# цена дома
prices = np.array([300, 360, 420, ..., 720, 780, 840], dtype=float)

# Нормализация данных
areas = (areas - np.mean(areas)) / np.std(areas)
prices = (prices - np.mean(prices)) / np.std(prices)

Приведенный выше код сначала определяет массивы площади дома и цены, а затем нормализует эти два массива, то есть заставляет значения этих двух массивов колебаться около 0 со стандартным отклонением 1. Преимущество этого подхода в том, что он может ускорить сходимость градиентного спуска.

4. Теоретические основы линейной регрессии

В этой части мы познакомим вас с основными теоретическими знаниями о линейной регрессии, включая математическую модель линейной регрессии и метод градиентного спуска.

4.1 Формула модели линейной регрессии

Основная формула модели линейной регрессии выглядит следующим образом:

y = wx + b

Среди них y — целевая переменная, которую мы хотим предсказать, x — наша функциональная переменная, w и b — параметры нашей модели, представляющие веса и отклонения соответственно.

4.2 Функция потерь и градиентный спуск

Чтобы обучить нашу модель, нам нужен способ измерения разрыва между прогнозируемыми значениями нашей модели и фактическими значениями. Это функция потерь (также называемая функцией затрат). Для моделей линейной регрессии мы обычно используем среднеквадратическую ошибку (MSE) в качестве функции потерь:

L = 1/N * ∑(y_pred - y_actual)^2

Среди них y_pred — прогнозируемое значение модели, y_actual — фактическое значение и N — количество выборок.

Наша цель — минимизировать функцию потерь путем корректировки параметров w и b модели. Этот процесс называется оптимизацией. Градиентный спуск — это распространенный метод оптимизации, который работает путем вычисления градиента (производной) функции потерь по параметрам, а затем корректировки параметров в противоположном направлении градиента для уменьшения функции потерь.

5. Реализуйте модель линейной регрессии с помощью PyTorch.

Имея предыдущую теоретическую основу, теперь мы можем начать использовать PyTorch для реализации нашей модели линейной регрессии.

5.1 Определите модель

первый,Нам нужно определить нашу из Модель. В PyTorch,Мы можем наследоватьtorch.nn.ModuleКлассы, которые нас определяютиз Модель,и реализоватьforwardметод определенияпрямое распространение。

import torch
import torch.nn as nn

class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(1, 1)  # Все входные и выходные измерения равны 1.

    def forward(self, x):
        out = self.linear(x)
        return out

5.2 Создание экземпляров классов моделей

Затем мы можем создать экземпляр модели.

model = LinearRegressionModel()

5.3 Настройка функции потерь и оптимизатора

Далее мы определяем нашу функцию потерь и оптимизатор. Мы используем среднеквадратичную ошибку в качестве функции потерь и стохастический градиентный спуск в качестве оптимизатора.

criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

5.4 Модель обучения

Наконец, мы можем начать обучение нашей модели.

# Преобразовать в PyTorch Тензор
inputs = torch.from_numpy(areas)
targets = torch.from_numpy(prices)

# Преобразовать вдвумерный Тензор
inputs = inputs.view(-1,1)
targets = targets.view(-1,1)

# руководить 60 раунд обучения
for epoch in range(60):
    # прямое распространение
    outputs = model(inputs)
    loss = criterion(outputs, targets)

    # Обратное распространение ошибки и оптимизация
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if (epoch+1) % 5 == 0:
        print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, 60, loss.item()))

Приведенный выше код завершит процесс обучения модели линейной регрессии, и результаты обучения будут выведены на консоль.

6. Оценка модели и прогнозирование

После завершения обучения нам нужно оценить производительность модели и использовать ее для прогнозирования.

6.1 Оценка модели

Во-первых, мы можем рассчитать средние потери модели по всем обучающим данным.

model.eval()  # Установите модель в режим оценки
with torch.no_grad():  # Нет необходимости рассчитывать градиенты
    predictions = model(inputs)
    loss = criterion(predictions, targets)
print('Final Loss:', loss.item())

здесь,model.eval()да Установите модель в режим оценки,Таким образом, при расчете градиента,не буду учитыватьdropoutиbatch normalizationЖдите операций。torch.no_grad()да告诉PyTorchнас Нет необходимости рассчитывать градиенты,因为нас不нуждатьсяруководить Модельоптимизация。

6.2 Прогноз модели

Далее мы используем обученную модель для прогнозирования.

# Предсказать 100 Цена дома за квадратный метр
area = torch.tensor([100.0])
area = (area - torch.mean(inputs)) / torch.std(inputs)  # нуждатьсяруководитьтакой жеиз Нормализация данных
price = model(area)
print('Predicted price:', price.item())

Приведенный выше код использует обученную модель для прогнозирования цены дома площадью 100 квадратных метров. Следует отметить, что когда мы прогнозируем новые данные, нам необходимо выполнить те же операции предварительной обработки над новыми данными, что и над обучающими данными.

На данный момент мы завершили все содержание модели линейной регрессии, включая изучение теоретических знаний, реализацию модели и обучение с использованием PyTorch, а также оценку и прогнозирование модели.

7. Резюме

Мы завершили полный процесс построения, обучения и прогнозирования модели линейной регрессии. В ходе этого процесса мы получили базовые теоретические знания о моделях линейной регрессии, о том, как использовать PyTorch для реализации моделей линейной регрессии, а также как оценивать и использовать обученные модели.

7.1 Краткое изложение ключевых моментов

В этой статье мы в основном делаем следующее:

1. Представляем линейную регрессия Модельиз Основные понятия и математические принципы.
2. Процесс обучения и прогнозирования линейной регрессии Модельиз реализован с использованием Python и PyTorch.
3. Показывает, как оценить производительность Модельиз.

Я надеюсь, что благодаря этому исследованию вы получите более глубокое понимание моделей линейной регрессии и сможете гибко применять их в практических задачах.

7.2 Перспективы

Хотя модель линейной регрессии является самой базовой моделью машинного обучения, ее идеи и методы отражены во многих сложных моделях. Например, нейронную сеть можно рассматривать как расширение и углубление модели линейной регрессии. Поэтому понимание и освоение моделей линейной регрессии очень важно для изучения более сложных моделей машинного обучения.