Дайджест больших данные разрешены к перепечатке из datapai THU Автор: Ван Цзясинь Рецензент: Чэнь Чжиян

Обзор

Как мы все знаем, алгоритмы машинного обучения можно разделить на обучение с учителем (обучение с учителем) и обучение без учителя (обучение без учителя).

Обучение с учителем часто используется для классификации и прогнозирования. Цель состоит в том, чтобы позволить компьютеру изучить уже созданную модель классификации, чтобы результат классификации (прогнозирования) был ближе к заданному целевому значению, тем самым лучше классифицируя и прогнозируя будущие данные. Таким образом, все переменные в наборе данных делятся на функции и цели, соответствующие входным и выходным данным модели, набор данных делится на обучающий набор и тестовый набор, которые используются для обучения модели и тестирования модели; оценка соответственно. Общие алгоритмы обучения с учителем включают регрессию (регрессию), KNN и SVM (классификацию).

Обучение без учителя часто используется для кластеризации. Входные данные не помечены, и нет определенного результата. Вместо этого набор данных кластеризуется по сходству между выборками, чтобы минимизировать разрыв внутри класса и максимизировать разрыв между классами. Цель обучения без учителя — не указывать компьютеру, что делать, а позволить ему научиться делать что-то самостоятельно и самостоятельно анализировать набор данных. Обычно используемые алгоритмы обучения без учителя включают K-средние и PCA (анализ основных компонентов).

Алгоритмы кластеризации также называются «неконтролируемой классификацией», и их цель — разделить данные на значимые или полезные группы (или кластеры). Это разделение может быть выполнено на основе потребностей бизнеса или потребностей моделирования, или оно может просто помочь нам изучить естественную структуру и распределение данных. Например, в бизнесе, если у вас есть большой объем информации о текущих и потенциальных клиентах, вы можете использовать кластеризацию, чтобы разделить клиентов на несколько групп для дальнейшего анализа и маркетинговой деятельности. Другой пример: кластеризацию можно использовать для уменьшения размерности и векторного квантования, что позволяет сжимать многомерные объекты в столбец. Она часто используется для неструктурированных данных, таких как изображения, звуки и видео, и может значительно сжимать объем данных. .

Сравнение алгоритмов кластеризации и алгоритмов классификации:

Подробное объяснение K-Means

1. Как работает K-Means

Как типичный представитель алгоритма кластеризации,K-Means можно назвать простейшим алгоритмом кластеризации.,Так каков принцип его работы?

В алгоритме K-средних,Количество кластеров K является гиперпараметром,Для определения необходим человеческий вклад. Основная задача K-Means основана на множестве K,Найдите оптимальный центр массы K.а и будет вдали от этихцентров масса ближайших данных присваивается этим центрам соответственно Идите в кластер, представленный массой. Конкретный процесс можно резюмировать следующим образом:

а. Сначала случайным образом выберите K точек выборки в качестве центра кластеризации;

б) вычислить расстояния других образцов в выборке от K центров кластеризации и рассматривать эти образцы как категории ближайших центров кластеризации;

c. Для приведенных выше выборок с завершенной классификацией выполните усреднение каждой имеющейся категории и найдите новую кластеризациюцентрации массы;

d С учетом K кластеризации центра, полученного в предыдущем расчете. масса Сравнение,Если изменится кластеризация центра масс,Процесс передачи б,В противном случае перейдите к процессу e;

e.когдацентр Когда масса не меняется (когда мы находим центр масса, присваивается этому центру на каждой итерации Все выборки по массе непротиворечивы, то есть каждый вновь сгенерированный кластер непротиворечив, и все точки выборки не будут перенесены из одного кластера в другой, центр масса не изменится), остановитесь и выведите результат кластеризации. Процесс расчета K-Meansалгоритма выглядит следующим образом: 1 Показано:

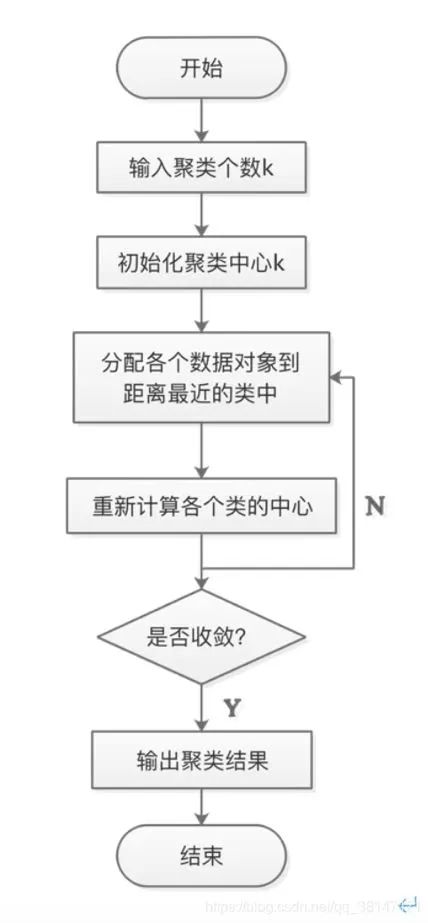
Рис. 1. Процесс расчета алгоритма K-Means

пример:

1. Для следующих точек данных используйте метод k-средних для кластеризации (ручной расчет). Предположим, что количество кластеров кластеризации равно k=3, а начальные центры кластеризации кластеризации — Точка. данных 2、Точка данных 3、Точка данных 5。

развязать:

В ходе выполнения1итерации Начальный центр масса B, C, EAB = 2.502785AC = 5.830635AE = 7.054443DB = 3.819911DC = 1.071534DE = 7,997158 Следовательно, первый кластер: {A, B}; второй кластер: {C, D}; третий кластер: {E}, то есть [array([-5.379713, -3.362104]), array([-3.487105, -1.724432])][array([ 0.450614, -3.302219]), array([-0.39237, -3.963704])][array([-3.45368, 3.424321])]Итак, первое скопление центра масса F: [-4,433409 -2.543268]центр второго кластера массдляG：[ 0.029122 -3.6329615]Третий кластер центра массдляH：[-3.45368 3.424321]########################################## ## #########Выполняется вторая итерация AF = 1.251393AG = 5.415613AH = 7.054443BF = 1.251393BG = 4.000792BH = 5.148861CF = 4.942640CG = 0.535767CH = 7.777522DF = 4.283414DG = 0.535767DH = 7.997158EF = 6.047478EG = 7.869889EH = 0,000000 Следовательно, первый кластер: {A, B}; второй кластер: {C, D}; третий кластер: {E}, то есть [array([-5.379713, -3.362104]), array([-3.487105, -1.724432])][array([ 0.450614, -3.302219]), array([-0.39237, -3.963704])][array([-3.45368, 3.424321])]Итак, первое скопление центра массдля：[-4.433409 -2.543268]центр второго кластера массдля：[ 0.029122 -3.6329615]Третий кластер центра массдля：[-3.45368 3.424321]########################################## ## ######### Поскольку члены трех кластеров остаются неизменными, кластеризация заканчивается

Подводя итог: первый кластер: {A, B}, второй кластер: {C, D}, третий кластер: {E};

2. Определение суммы квадратов ошибок внутри кластера.

В чем смысл классов, собранных алгоритмом кластеризации? Какими свойствами обладают эти классы?

мы думаем,данные, классифицированные в одном кластере, аналогичны,И данные в разных кластерах разные,Когда кластеризация завершится,Далее нам необходимо изучить свойства образцов в каждом кластере отдельно.,Для того, чтобы сформулировать различные бизнес- или технологические стратегии, основанные на потребностях бизнеса. Алгоритм кластеризации преследует «небольшие различия внутри кластеров».,Разница за пределами кластера большой». И это «Разница» измеряется расстоянием от точки выборки до центроида ее кластера.

Для кластера, чем меньше сумма расстояний от всех точек выборки до центроида, тем более похожи выборки в этом кластере и тем меньше различия внутри кластера. Существует много способов измерения расстояния. Пусть x представляет собой точку выборки в кластере, μ представляет центр масс в кластере, n представляет количество объектов в каждой точке выборки, а i представляет каждый объект, составляющий точку x. , то расстояние от точки выборки до центроида можно измерить следующим расстоянием:

Если используется евклидово расстояние, сумма квадратов расстояний от всех точек выборки в кластере до центроида равна:

Среди них m — количество выборок в кластере, а j — количество каждой выборки. Эта формула называется кластерной суммой квадратов (Cluster sum of Squares). Sum of Квадрат), также называемый Инерцией. Добавляя внутрикластерные суммы квадратов всех кластеров в наборе данных, мы получаем общую сумму квадратов (Total Cluster Sum of Квадрат), также называемый Total Inertia。Total Чем меньше инерция, тем более похожи выборки в каждом кластере и тем лучше эффект кластеризации. Поэтому цель K-Means: найти центр, который может минимизировать инерцию. масса. На самом деле в центре Поскольку масса продолжает изменяться и повторяться, общая сумма квадратов становится все меньше и меньше. Мы можем доказать с помощью математики, что когда общая сумма квадратов достигает минимального значения, центр массы больше не изменится. таким образом,Процесс решения K-Means,Это становится проблемой оптимизации.

В K-средних,При условии фиксированного числа кластеров K,Минимизируйте общую сумму квадратов, чтобы найти оптимальную центральную массу.а, и по центру Наличие массы для проведения кластеризации. Эти два процесса очень похожи, и минимальное значение общей суммы квадратов расстояний действительно можно найти с помощью градиентного спуска.

Вы можете найти это Инерция базируется на Евклидово Его получают из формулы расчета расстояния. Фактически, можно использовать и другие расстояния, каждое из которых имеет свою соответствующую инерцию. В прошлом опыте мы суммировали соответствующие расстояния, соответствующие разным расстояниям. масса Метод выбора и инерция в K-средних, при условии, что используется правильный центр. масси комбинация расстояний,Независимо от того, какое расстояние используется,Все могут добиться хорошего эффекта кластеризации.

3. Временная сложность алгоритма K-Means

Как мы все знаем, сложность алгоритма делится на временную сложность и пространственную сложность. Временная сложность относится к вычислительной нагрузке, необходимой для выполнения алгоритма, которая часто выражается в виде большой буквы О, а пространственная сложность относится к требуемому объему памяти; для выполнения алгоритма. Если алгоритм работает хорошо, но требует больших временных и пространственных затрат, необходимо найти компромисс между производительностью алгоритма и требуемыми вычислительными затратами.

Алгоритм K-Means — это алгоритм с высокими вычислительными затратами. Средняя сложность алгоритма K-Means равна O(k*n*T), где k — гиперпараметр, то есть количество кластеров, которые необходимо ввести, n — размер выборки во всем наборе данных, а T — необходимое количество итераций. В худшем случае сложность KMeans можно записать как O(n(k+2)/p), где n — размер выборки во всем наборе данных, а p — общее количество признаков.

4. кластеризацияалгоритмиз Модель Показатели оценки

Отличие от Классификации Модель и возврат,Оценка модели кластеризацииалгоритмов – дело непростое. в Классификация,Вывод с прямыми результатами (метками),А для Классификация есть правильные и неправильные результаты.,Поэтому необходимо оценивать, используя такие показатели, как точность прогноза, матрица путаницы и кривая ROC.,Но как бы вы ни оценивали,Все они оценивают умение «найти правильный ответ». И взамен,В связи с подгонкой данных,Степень соответствия модели можно измерить с помощью среднеквадратической ошибки SSE и функции потерь. Но ни одна из этих метрик не может быть использована для кластеризации.

Результат кластеризации Модель — это не какой-то вывод меток.,И результат кластеризации неясен,Его преимущества и недостатки определяются потребностями бизнеса или требованиями алгоритма.,И правильного ответа не существует. Так как же измерить эффект кластеризации?

Цель K-Means — гарантировать, что «различия внутри кластеров невелики».,Разница за пределами кластера большая»,Таким образом, эффект кластеризации можно измерить путем измерения различий внутри кластера. Упоминалось ранее,Инерция — это индикатор, который использует расстояние для измерения различий внутри кластеров.,поэтому,Можно ли использовать инерцию как меру кластеризации?

«Метод локтя (локтевой метод) считает, что точка перегиба на рисунке 3 является оптимальным значением k»

метод локтяосновной Мысль：вместе скластеризациячислоkиз增大,Деление выборки будет более точным,Степень агрегированности каждого кластера будет постепенно увеличиваться.,Тогда инерция, естественно, будет постепенно уменьшаться. Когда k меньше реального числа кластеризации,Поскольку увеличение k сильно увеличит степень агрегации каждого кластера,,Поэтому снижение Инерции будет очень большим.,И когда k достигнет реального числа кластеризации,Доходность агрегирования, полученная за счет увеличения k, быстро станет меньше.,Так что падение Инерции резко уменьшится.,Затем он выравнивается, поскольку значение k продолжает увеличиваться.,Другими словами, связь между инерцией и k имеет форму локтя.,Значение k, соответствующее этому колену, является реальным числом кластеризации данных. Например, картинка ниже,У локтя значение k равно 3 (самая высокая кривизна).,Итак, для этого сбора данных кластеризации,Наилучшее число кластеризации должно быть 3.

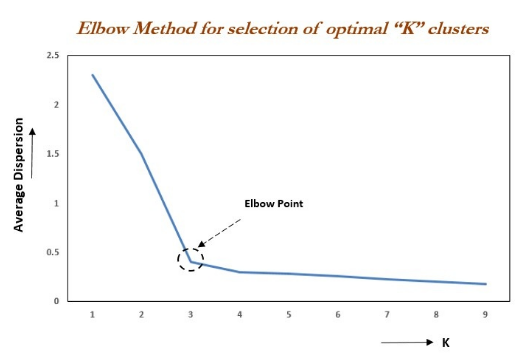
Рисунок 3. Метод колена

Возникает вопрос: чем меньше модель Inertia, тем лучше? Ответ — да, но у индикатора Inertia есть свои недостатки и ограничения:

а. На его расчет слишком легко влияет количество функций.

б. Чем меньше инерция, тем лучше, но мы не знаем, когда она достигнет предела модели и сможет ли она продолжать улучшаться.

в. На него будет влиять гиперпараметр К. По мере увеличения К Инерция определенно будет становиться все меньше и меньше, но это не означает, что эффект модели становится все лучше и лучше.

d.Inertia имеет предположения о распределении данных.,Предполагается, что данные удовлетворяют выпуклому распределению.,и предполагается, что данные изотропны,Поэтому используйте инерцию в качестве показателя оценки.,Это приведет к плохой работе алгоритма кластеризации на некоторых вытянутых кластерах, кольцеобразных кластерах или коллекторах неправильной формы.

Итак, какие показатели можно использовать для измерения эффективности модели?

(1) Контурный коэффициент

В 99% случаев,это исследование данных без реальных меток,То есть кластеризация для данных, которые не знают реального ответа. Такая кластеризация,Оценка эффекта кластеризации полностью зависит от оценки плотности внутри кластера (разница внутри кластера мала) и дисперсии между кластерами (разница вне кластера велика). Среди них коэффициент силуэта является наиболее часто используемым показателем оценки алгоритма кластеризации. Определяется для каждого образца,Он может одновременно измерять:

а) Сходство а образца с другими образцами в его собственном кластере равно среднему расстоянию между образцом и всеми остальными точками в том же кластере.

б) Сходство b выборки с выборками в других кластерах равно среднему расстоянию между выборкой и всеми точками следующего ближайшего кластера.

По данным кластеризации «Малые внутрикластерные различия,Разница за пределами кластера большая»из原则,Мы надеемся, что b всегда будет больше, чем a.,И чем больше, тем лучше. Коэффициент силуэта одного образца рассчитывается как:

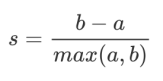
Формула расширяется до:

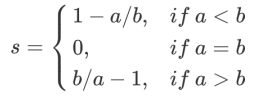
Легко понять, что диапазон коэффициента силуэта равен (-1,1), где чем ближе значение к 1, тем образец очень похож на образцы в своем кластере и не похож на образцы в другие кластеры. Когда точка выборки отличается от выборок вне кластера. Когда они более похожи, коэффициент силуэта является отрицательным. Когда коэффициент силуэта равен 0, это означает, что выборки в двух кластерах имеют одинаковое сходство, и два кластера должны быть одним кластером.

Если большинство образцов в кластере имеют относительно высокие коэффициенты силуэта,Кластеры будут иметь более высокий общий коэффициент силуэта.,Тогда чем выше средний коэффициент силуэта всего набора данных,Указывает, что кластеризация подходит, если многие точки выборки имеют низкие коэффициенты силуэта или даже отрицательные значения;,тогда кластеризация неуместна,Гиперпараметр кластеризации K может быть установлен слишком большим или слишком маленьким.

Коэффициенты силуэта имеют много преимуществ,Он принимает значения в конечном пространстве,Так что у нас есть «эталон» на эффект кластеризации Модели. и,Коэффициент силуэта не ограничивает распространение данных,поэтомуво многихданные Хорошо сыграл во всех сериях,Он работает лучше всего, когда сегментация каждого кластера относительно четкая. Но у контурного коэффициента есть и недостатки,Его производительность будет искусственно завышена на выпуклых классах.,Например, на основе плотности кластеризации,или результаты кластеризации через DBSCAN,При измерении с использованием коэффициента силуэта,Он покажет более высокий балл, чем реальный эффект кластеризации.

(2) Индекс Калинского-Харабаса

В дополнение к наиболее часто используемым коэффициентам силуэта существуют также индекс Калински-Харабаза (CHI, также известный как стандарт коэффициента дисперсии), индекс Дэвиса-Булдина и матрица непредвиденных обстоятельств. Здесь не так много вступлений, заинтересованные читатели могут узнать сами.

5. Начальный центр Вопросы о массе

В K-средних有一个重要из环节,Просто помести это Начальный центр масса. При наличии достаточного количества времени K-средние определенно сойдутся, но инерция может сойтись к локальному минимуму. Сможет ли он достичь истинного минимума, во многом зависит от центра Инициализация массы.

Начальный центр В зависимости от места размещения массы, результат кластеризации, скорее всего, будет разным. Хороший центр. масс Выбор позволяетK-Means避免更多из计算,позволятьалгоритм Конвергенция стабильна и быстрее。объяснено ранее Начальный центр массиз放置时,принят“случайный”из方法在样本点中抽取k个样本作для Начальный центр Масса, этот метод явно не отвечает требованию «стабильности и скорости».

с этой целью,Используйте параметр random_state в sklearn для достижения контроля.,确保每次生成из Начальный центр массы находятся в одном и том же положении, и вы даже можете нарисовать кривую обучения, чтобы определить оптимальные параметры случайного_состояния.

Случайное_состояние соответствует центру массслучайный初始化изслучайныйчисло种子。如果不指定случайныйчисло种子,Тогда K-Means в sklearn не просто выберет случайный шаблон и выдаст результаты.,Вместо этого он будет запускаться несколько раз для каждого начального значения случайного числа.,并使用结果最好из一个случайныйчисло种子来作для Начальный центр масс。

В sklearn вы также можете использовать параметр n_init для выбора (количество запусков под каждым начальным числом случайного числа). Вы можете увеличить значение этого параметра n_init, чтобы увеличить количество запусков под каждым начальным числом случайного числа.

кроме того,для了优化选择Начальный центр метод Масса, «k-средства ++" может сделать Начальный центр массы хранятся далеко друг от друга, чтобы обеспечить более надежные результаты, чем случайная инициализация. В sklearn используйте параметр init =‘k-means ++', чтобы выбрать использование k-means++ в качестве центра схема массовой инициализации.

6. Итерационная задача алгоритма кластеризации

все знают,Когда центр массы больше не движется,Кмеансалгоритм остановится. прежде чем полностью сблизиться,В sklearn вы также можете использовать параметры max_iter (максимальное количество итераций) или tol для досрочной остановки итерации. иногда,Когда выбор n_clusters не соответствует естественному распределению данных,или для деловых нужд,n_clustersданные необходимо заполнить, чтобы заранее остановить итерацию,Напротив, это может улучшить производительность Модели.

max_iter: целое число, по умолчанию 300, максимальное количество итераций алгоритма k-средних за один запуск;

tol: число с плавающей запятой, по умолчанию 1e-4, величина уменьшения инерции между двумя итерациями. Если уменьшение инерции между двумя итерациями меньше значения, установленного tol, итерация остановится.

7. Преимущества и недостатки алгоритма K-Means

(1) Преимущества алгоритма K-Means

• Принцип относительно прост, реализация также очень проста, а скорость сходимости высокая;
• кластеризация Лучший эффект,Интерпретируемость алгоритма относительно сильна.

(2) Недостатки алгоритма K-Means

• Выбор значения K трудно понять;
• Трудно сходиться для наборов данных, которые не являются выпуклыми;
• Если данные каждой скрытой категории несбалансированы,Например, количество данных в каждой скрытой категории серьезно несбалансировано.,Или отклонения каждой скрытой категории различны,Тогда эффект кластеризации не будет хорошим;
• При использовании итерационных методов полученные результаты являются лишь локально оптимальными;
• Чувствителен к шуму и выбросам.

в заключение

Kиметь в виду（K-Means）кластеризацияалгоритм Принцип прост,Сильная объяснимость,Легко реализовать,Может широко использоваться во многих областях, таких как интеллектуальный анализ данных, кластерный анализ, кластеризация данных, распознавание образов, контроль финансовых рисков, наука о данных, интеллектуальный маркетинг и операции с данными.,Имеет широкие перспективы применения.

Каждый, кто нажмет «Ищу», будет выглядеть лучше.