окартинавычислить&картина Обзор основ обучения：Изучение необходимых знаний（Paddle Graph Learning (PGL)）

добро пожаловатьforkОригинальная ссылка на этот проект：окартинавычислить&картина Обзор основ обучения：Изучение необходимых знаний（Paddle Graph L）https://aistudio.baidu.com/aistudio/projectdetail/4982973?contributionType=1

Из-за нехватки места я поместил в главу 3 только часть программы. Если вам это нужно, вы можете самостоятельно форкнуть исходную ссылку проекта.

0.1 Основные понятия графовых вычислений

Сначала посмотрите определение в энциклопедии Baidu:

Обработка графов (Graph Processing) заключается в моделировании данных в виде графика для получения результатов, которые в прошлом было трудно получить с плоской точки зрения.

Граф — это абстрактная структура данных, используемая для представления связей между объектами. Он описывается с помощью вершин и ребер: вершины представляют объекты, а ребра представляют отношения между объектами. Данные, которые можно абстрагировать в граф, называются данными графа. Графовые вычисления — это процесс использования графов в качестве моделей данных для выражения и решения проблем. Системное программное обеспечение, предназначенное для эффективного решения задач графовых вычислений, называется системой графовых вычислений.

В эпоху больших данных между данными существуют корреляции. Поскольку графы представляют собой организационные структуры, которые выражают сложные отношения между вещами, многие сценарии применения в реальной жизни требуют использования графов, таких как графики отношений друзей-пользователей Taobao, дорожные карты, принципиальные схемы, сети передачи вирусов, State Grid и литературные сети. социальная сеть и граф знаний.

Чтобы получить полезную информацию из корреляций между этими данными, один за другим появляется большое количество графовых алгоритмов. Они получают важную информацию, скрытую в данных графа, посредством итеративной обработки больших данных графа. Будучи основной технологией искусственного интеллекта следующего поколения, графовые вычисления широко используются во многих областях, таких как здравоохранение, образование, армия и финансы. Они привлекли внимание правительств, глобальных научно-исследовательских институтов и гигантских компаний. теперь стал новым рубежом в глобальной технологической конкуренции.

0.1.1 Расчет графика

• Графики могут связывать различные типы данных: объединять данные из разных источников и типов в один и тот же график для анализа и получать результаты, которые в противном случае было бы трудно обнаружить с помощью независимого анализа;
• Представление изображения может сделать многие проблемы более эффективными: например, путь、подключен Порции и т. д.,Только расчетный метод картины может дать наиболее эффективный результат. Однако,У компьютерных вычислений есть некоторые проблемы и характеристики, которые отличают их от других типов вычислительных задач:
• Много произвольного доступа: вычисления изображений вращаются вокруг топологии изображений.,Процесс расчета будет иметь доступ к стороне и двум связанным вершинам.,Но из-за редкого характера фактических данных о фотографиях (обычно лишь несколько приезжающих и несколько сотен номеров средней степени),Неизбежно генерируется большое количество случайных доступов;
• Неточности в расчетах: фактические данные изображения имеют характеристики распределения по степенному закону.,То есть число степеней большинства вершин очень мало.,Очень немногие вершины имеют большие номера степеней (например, поклонники звездных пользователей в существующей линейке социальная сеть).,Это затрудняет разделение вычислительных задач.,Очень легко вызвать дисбаланс нагрузки.

0.1.2 Графовая вычислительная система

Поскольку масштаб графовых данных продолжает расти, требования к возможностям графовых вычислений становятся все выше и выше. На этом фоне родилось большое количество вычислительных систем, специально ориентированных на обработку графовых данных.

Pregel, разработанный Google, является пионером в области специализированных графовых вычислительных систем. Прегель предложил модель вершинно-центрированного программирования, разбивая процесс анализа графа на несколько раундов вычислений. В каждом раунде каждая вершина независимо выполняет свою собственную вершинную программу, а статус между вершинами синхронизируется посредством передачи сообщений. Giraph — это реализация Pregel с открытым исходным кодом. Основанная на Giraph, Facebook использует 200 машин для анализа данных графа на уровне триллиона ребер, и расчет одного раунда PageRank занимает почти 4 минуты.

GraphLab создан в лаборатории CMU и основан на механизме общей памяти, который позволяет пользователям использовать асинхронные вычисления для ускорения сходимости определенных алгоритмов. PowerGraph оптимизирован на основе GraphLab. Основываясь на степенных характеристиках распределения степеней вершин в реальных данных графа, PowerGraph предлагает идею секционирования вершин, которая позволяет добиться более детального секционирования данных и лучшей балансировки нагрузки. Его вычислительная модель также используется в последующих системах графовых вычислений, таких как GraphX.

Хотя упомянутые выше системы графовых вычислений имеют значительно улучшенную производительность по сравнению с MapReduce, Spark и т. д., их вычислительная эффективность всё равно очень низка, уступая даже тщательно оптимизированным однопоточным программам.

Gemini была предложена командой факультета компьютерных наук Университета Цинхуа. Учитывая ограничения существующих систем, Gemini предложила концепцию проектирования, ориентированную на вычисления, за счет сокращения накладных расходов, вызванных распределением, и оптимизации реализации локальной вычислительной части. насколько это возможно, система может быть использована в условиях масштабируемости без потери эффективности [5]. Для различных характеристик графовых вычислений Gemini предложила соответствующие меры оптимизации в области сжатия данных, разделения графа, планирования задач, переключения режима связи и т. д., что на порядок быстрее, чем самая быстрая производительность других известных систем графовых вычислений. . ShenTu следует и расширяет модель программирования и вычислений Gemini и может использовать десятки миллионов ядер вычислительных ресурсов машины Sunway TaihuLight для эффективной обработки сверхкрупномасштабных графических данных с 70 триллионами ребер. Он был включен в шорт-лист премии Gordon 2018 года. Список финалистов Bell Award.

Помимо использования масштабируемых распределенных графовых вычислительных систем для обработки графовых данных, объем которых превышает объем памяти одной машины, существуют также некоторые решения для выполнения крупномасштабных графовых вычислительных задач за счет эффективного использования внешней памяти на одной машине. Среди представителей есть GraphChi. , X-Stream, FlashGraph, GridGraph, Mosaic и т. д.

0.2 Рисунок Ключевые технологии

0.2.1 Организация графических данных

Из-за разреженности реальных графов графовые вычислительные системы обычно используют методы хранения разреженных матриц для представления данных графа. Двумя наиболее часто используемыми из них являются CSR (сжатая разреженная строка) и CSC (сжатая разреженная строка), которые хранятся в строках (столбцах). ) соответственно. Каждая строка (столбец) содержит столбец (строку) ненулевого элемента, а каждая строка (столбец) соответствует исходящему ребру (входящему ребру) вершины.

0.2.2 Разделение данных графика

Разделение большого графа на несколько более мелких подграфов — это метод, используемый многими графовыми вычислительными системами для расширения масштаба обработки. Кроме того, разделение графа также может повысить локальность данных, тем самым уменьшая случайность доступа к памяти и повышая эффективность системы. Для распределенных графовых вычислительных систем разделение графа преследует две цели:

1. Размер каждого подграфа максимально схож, чтобы получить более сбалансированную нагрузку.
2. Зависимости между различными подизображениями (например, между сторонами подизображения) должно быть как можно меньше.,Уменьшите накладные расходы на связь между машинами.

Существует два способа разделения графов: деление по вершинам и деление по ребрам. Каждый из них имеет свои преимущества и недостатки:

1. Разделение вершин позволяет стороне, смежной с каждой вершиной, существовать на одной машине.,Так что локальность расчета лучше,Однако из-за степенного закона распределения чисел степеней может возникнуть дисбаланс нагрузки.
2. боковое разделение может в наибольшей степени решить проблему дисбаланса нагрузки,Однако каждую вершину необходимо разделить на несколько копий и распределить по разным машинам.,Поэтому вводятся дополнительные издержки синхронизации/пространства.

Все Pregel-подобные системы используют деление вершин, а PowerGraph/GraphX ​​— деление рёбер. Gemini использует метод, основанный на секционировании вершин, чтобы избежать чрезмерных накладных расходов на распределение, однако он опирается на идею секционирования ребер в режиме вычислений, распределяя вычисление каждой вершины на несколько машин отдельно и делая его максимально простым; Объем вычислений на каждой машине аналогичен, что устраняет проблему дисбаланса нагрузки, которая может быть вызвана секционированием вершин.

0.2.3 Планирование вершинных программ

В модели вершинно-ориентированных графовых вычислений каждая вершинная программа может планироваться параллельно. Большинство систем графовых вычислений используют метод синхронного планирования, основанный на модели BSP, который делит процесс вычислений на несколько супершагов (каждый супершаг обычно соответствует одной итерации). Все вершинные программы на каждом супершаге выполняются независимо и параллельно. .Глобальная синхронизация. Вершинные программы могут генерировать сообщения, которые отправляются другим вершинам, но процесс связи обычно отделен от процесса вычислений.

Проблемы, которые легко возникают при синхронном планировании:

1. При возникновении дисбаланса нагрузки,Тогда самый медленный вычислительный блок замедлит общий прогресс.
2. Некоторые алгоритмы могут не сходиться при существующей синхронизации.

По этой причине некоторые системы графовых вычислений предоставляют варианты асинхронного планирования, позволяющие каждой вершинной программе выполняться более свободно. Например, каждая вершинная программа может устанавливать приоритет, так что вершинные программы с высоким приоритетом могут выполняться с более высокой частотой. сходятся быстрее. Однако асинхронное планирование усложняет конструкцию системы, например, обеспечение согласованности данных, агрегирование сообщений и т. д., и во многих случаях эффективность не идеальна. Поэтому большинство графовых вычислительных систем по-прежнему используют синхронное планирование; некоторые системы, поддерживающие асинхронные вычисления, также используют синхронное планирование по умолчанию;

0.2.4 Модели вычислений и связи

Режимы связи, используемые графовыми вычислительными системами, в основном делятся на два типа: push и pull:

1. В режиме push каждая вершина передает сообщения соседним вершинам по стороне.,Соседние вершины обновляют свой статус на основе полученных сообщений. Почти все системы, подобные Pregel, используют эту модель вычислений и связи.
2. Режим Pull обычно делит вершины на мастер-копии и зеркальные копии.,Связь происходит между двумя типами реплик каждой вершины, а не между двумя вершинами каждого бокового соединения. GraphLab, PowerGraph, GraphX ​​и т. д. используют эту модель.

В дополнение к различным режимам связи, push и pull также имеют разные вычислительные компромиссы:

1. Режим Push может вызвать конкуренцию данных, требующую использования блокировок или атомарных операций для обеспечения правильности обновлений состояния.
2. Режим извлечения, хотя и не вызывает конфликтов, может привести к дополнительному доступу к данным.

Gemini объединяет два режима и адаптивно выбирает более подходящий режим на основе конкретных условий, участвующих в каждом раунде итерационных вычислений.

0.3 Приложения для графовых вычислений

0.3.1 Сортировка веб-страниц

Используя веб-страницы в качестве вершин и гиперссылки между веб-страницами в качестве ребер, весь Интернет можно смоделировать как очень огромный граф (десять триллионов ребер). Когда поисковые системы возвращают результаты, помимо рассмотрения релевантности веб-контента и ключевых слов, им также необходимо учитывать качество самой веб-страницы.

PageRank — это самый ранний алгоритм, используемый Google для ранжирования веб-страниц. Он указывает на важность веб-страниц, рассматривая ссылки как голоса. Процесс расчета PageRank не сложен: перед началом первого раунда итерации все вершины устанавливают свое значение PageRank равным 1, в каждом раунде итерации каждая вершина передает свое текущее значение PageRank, деленное на количество исходящих ребер, всем соседям как; голосование. Затем все голоса, полученные от соседей, суммируются как новое значение PageRank; это повторяется до тех пор, пока изменение значения PageRank всех вершин между двумя соседними раундами не достигнет определенного порога.

0.3.2 Открытие сообщества

Социальная сеть также представляет собой типичные данные графа: вершины представляют людей, а ребра представляют межличностные отношения; более широкие социальные сети также могут включать в себя объекты, связанные с людьми, такие как мобильные телефоны, адреса, компании и т. д. Обнаружение сообществ — это классическое применение анализа социальных сетей: граф разделяется на несколько сообществ, при этом вершины внутри каждого сообщества имеют более тесные связи, чем вершины за пределами сообщества. Открытие сообщества имеет очень широкий спектр применений и имеет соответствующие применения в большом количестве сценариев, таких как контроль финансовых рисков, национальная безопасность и общественное здравоохранение.

Распространение теговявляется широко используемымоткрытие сообществаалгоритм：Метка каждой вершины — это собственное сообщество.,Инициализация устанавливает собственный номер вершины, существующий на каждой последующей итерации;,Каждая вершина устанавливает наиболее часто встречающуюся метку среди своих соседей в качестве своей новой метки, когда изменение меток всех вершин между двумя соседними раундами меньше определенного порога, итерация останавливается;

0.3.3 Кратчайший путь

Поиск кратчайшего пути между вершинами графа — очень распространенная вычислительная задача графа. По размеру набора начальных и целевых вершин его можно разделить на одиночные (одна вершина к одной вершине) и множественные. пары (от нескольких вершин ко многим вершинам), один источник (от одной вершины ко всем остальным вершинам), мультиисточник (от нескольких вершин ко всем остальным вершинам), все пары (от всех вершин ко всем остальным вершинам) и т. д. Для невзвешенных графов обычно используются алгоритмы на основе BFS, для взвешенных графов более распространены алгоритм SPFA, алгоритм Беллмана-Форда и т. д.

Кратчайший путь имеет широкий спектр использования: в графах знаний часто необходимо найти кратчайший путь связи между двумя сущностями на основе черного списка и связи между сущностями, можно найти расстояние между другими вершинами и черным списком; и все пары точек. Кратчайший путь может помочь измерить положение (центральность) каждой вершины в топологии всего графа.

Задачи уровня узла：Финансовое мошенничество раскрыто,узел — пользователь и продавец,сторона — взаимодействие между пользователями и продавцами,Используйте картину Модель, чтобы предсказать потенциальных финансовых мошенников. существуют корпус обнаружения целей,Расстояние между точками в трехмерных данных облака точек каксторона,Обнаружение 3D-целей возможно благодаря структуре изображения.

Задачи побочного уровня：в системе рекомендаций,Установите взаимосвязь поведения пользователей с помощью существующих данных о пользователях и продуктах.,Получите векторное представление места проживания.,Затем выполните рекомендательное задание

задачи уровня графа：Идентификация запаха,использоватькартинанейронная сеть распознает молекулярные структуры и, следовательно, чувствует запахи

1. Картинки и обучение по картинкам

1.1 Основной метод представления графика

Давайте сначала кратко изучим основные понятия теории графов, классические алгоритмы теории графов и развитие обучения графов в последние годы.

Например, простая диаграмма может выглядеть так:

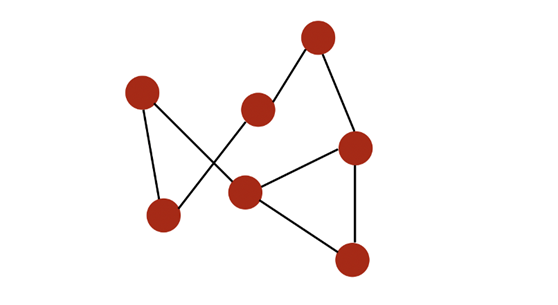
Узлы отмечены красным и соединены черными краями.

Диаграммы могут использоваться для представления:

• социальная сеть
• веб-страница
• биологическая сеть
• …

Какой анализ мы можем выполнить на графиках?

• Изучите топологию и связность
• Групповое обнаружение
• Узел идентификационного центра
• Предсказать отсутствие узла
• Предсказать недостающую сторону
• …
• Граф G=(V, E) состоит из следующих элементов:
• группаузел（такженазывается verticle）V=1,…,n
• группасторона E⊆V×V
• сторона (i,j) ∈ E Подключено узлом i и j
• i и j называетсясоседний узел（neighbor）
• узелизстепень（degree）относится ксоседний узелизколичество

[Не удалось передать изображение по внешней ссылке. Исходный сайт может иметь механизм защиты от кражи. Рекомендуется сохранить изображение и загрузить его напрямую (img-g583AsUR-1667871466119) (https://s2.51cto.com/images/blog). /202211/08091854_6369ae7e037aa19406.pn g?x-oss-process=image/watermark,size_14,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_100,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=)]

Принципиальная схема узлов, ребер и градусов

• Если все узлы изображения имеют n-1 индивидуальныйсоседний узел,тогдакартинадаполный（complete）。также Сразудаскажи всеузелвсе возможностииз Способ подключения。
• от i приезжать j Путь (path) относится к от i приезжатьдостигать j изсторонаизпоследовательность。ДолженДлина пути（length）равныйпрошел мимоколичество сторон。
• Диаметр фигуры（diameter）относится к连接任意两индивидуальныйузелизвсекратчайший Длина самого длинного пути в пути.

Например, в этом случае мы можем вычислить некоторый кратчайший путь, соединяющий любые два узла. Диаметр графа равен 3, поскольку ни один кратчайший путь между любыми двумя узлами не длиннее 3.

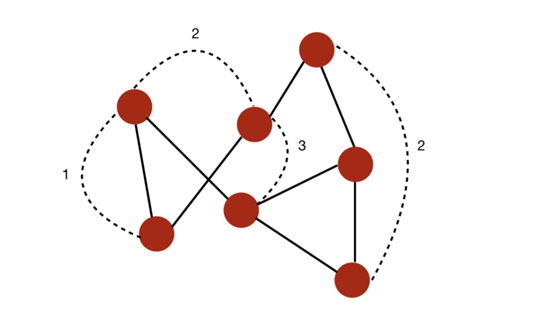
Граф диаметром 3

• геодезический путь（geodesic путь) относится к кратчайшему пути между двумя узлами. путь。
• Если все узлы могут соединяться друг с другом по определенному пути,тогда они образуютподключенная ветка（connected компонент). Если у изображения только одна подключенная ветка,тогдакартинадаподключениз（connected）

Например, вот график с двумя разными связанными ветвями:

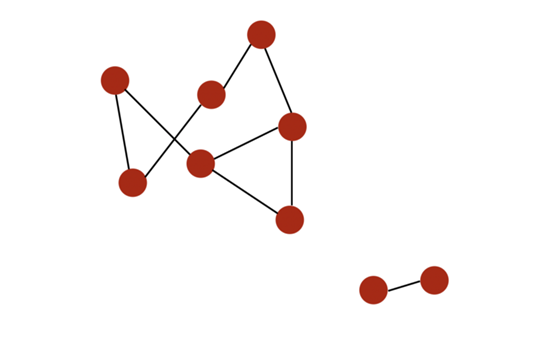
Граф с двумя связанными ветвями

• Если сторона изображения является упорядоченной парой,тогдакартинаданаправленный（directed）。i извходитьстепень（in-degree）относится к К i количество сторон,внестепень（out-degree）дадержаться подальше i количество сторон

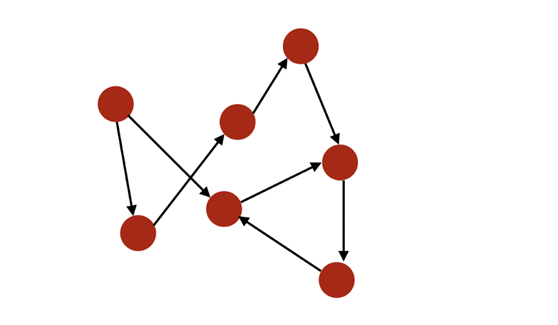
ориентированный граф

• Если можно вернуться приехать в данный узел,тогдакартинадаокольцованный（cyclic）。относительно,Если хотя бы один узел не может вернуться приехать,тогдакартина Сразудаациклический（acyclic）。
• картинаможет бытьВзвешенный（weighted）,о фильмах о новых фильмах о фильмах Весил тяжело.
• Если количество картины меньше количества узла,тогдакартинадаредкийиз（sparse）。относительно,Если между узлом много сторон,тогдакартинадаПлотныйиз（dense）

Книга Neo4J по графовым алгоритмам дает четкое и краткое изложение:

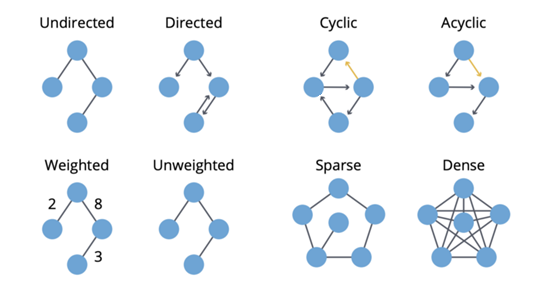
Резюме (от Neo4J Graph Book & Вклад босса Самооценки 3)

1.2 Хранение фотографий

Существует три способа хранения графов: матрица смежности, список смежности и перекрестный список.

1.2.1 Матрица смежности

ориентированный графиз Матрица смежности

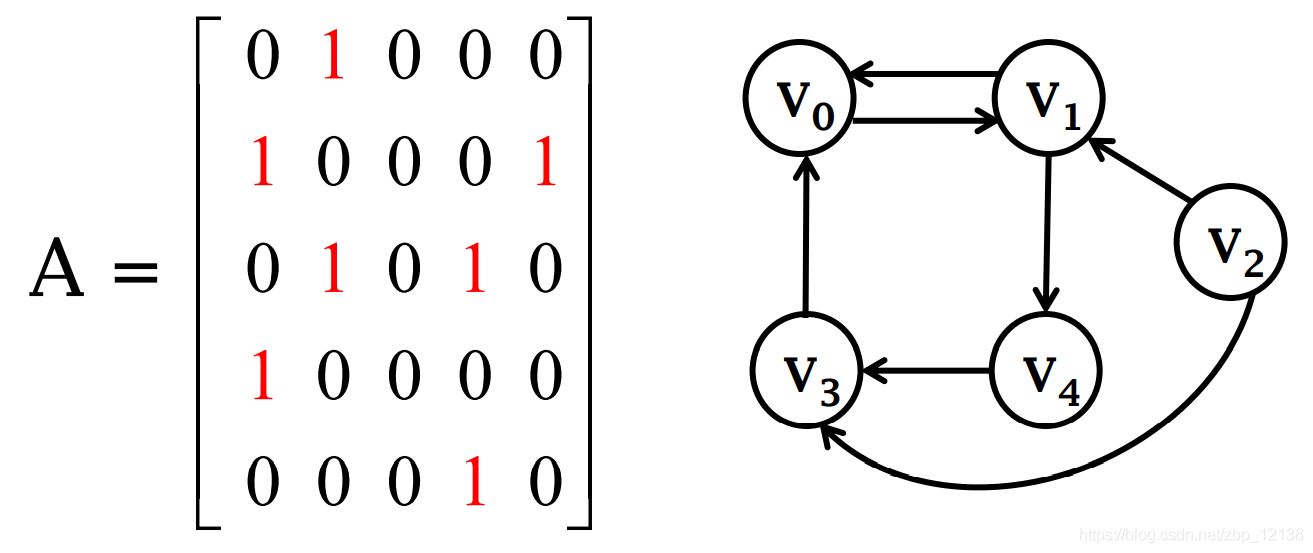
Матрица смежности неориентированного графа

• Используя матрицу смежности, существование обычно загружается в память следующим образом:

Для каждой возможной пары в графе установите значение 1, если два узла соединены ребром. Если граф неориентированный, то A симметричен.

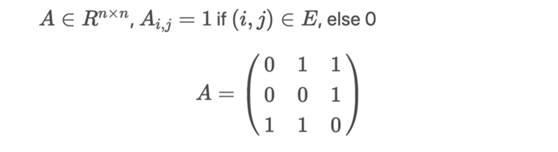
1.2.2 Список смежности

Для разреженных графов можно использовать метод хранения списка смежности:

При меньшем количестве ребер в соседней матрице будет большое количество нулевых элементов. Нулевые элементы соседней матрицы будут занимать много места и времени для хранения.

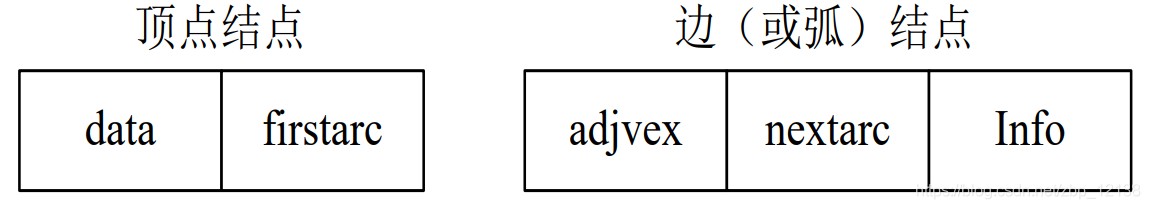
Представление списка смежности неориентированного графа

Одно и то же ребро неориентированного графа дважды появляется в списке смежности.

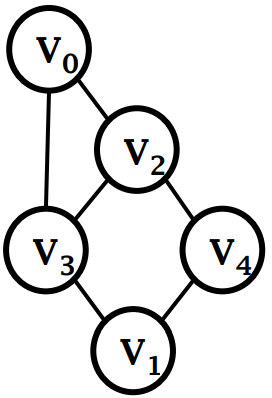
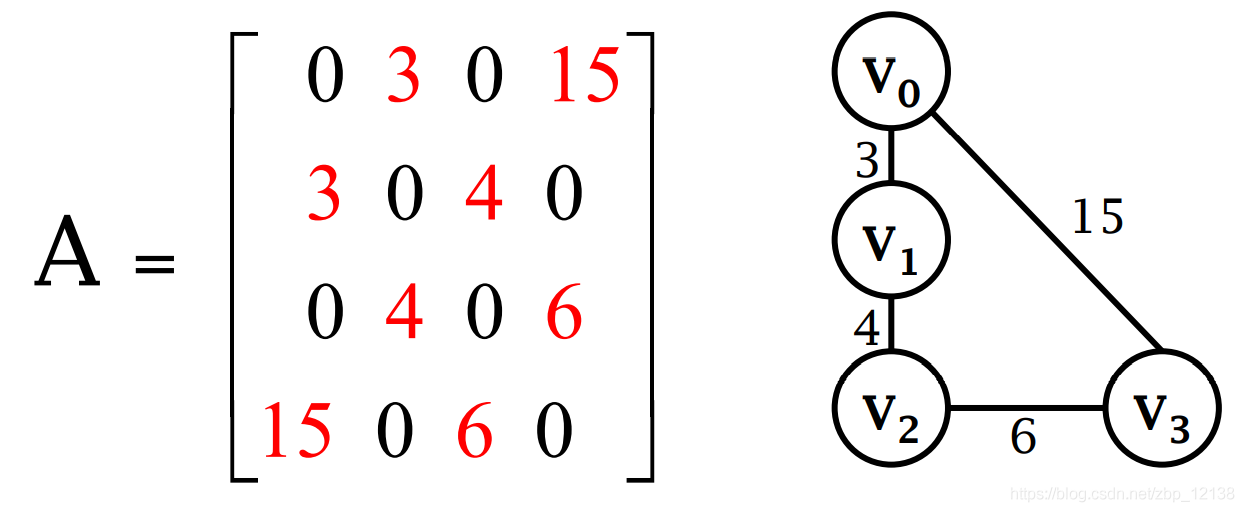
Приведенный выше график можно выразить как:

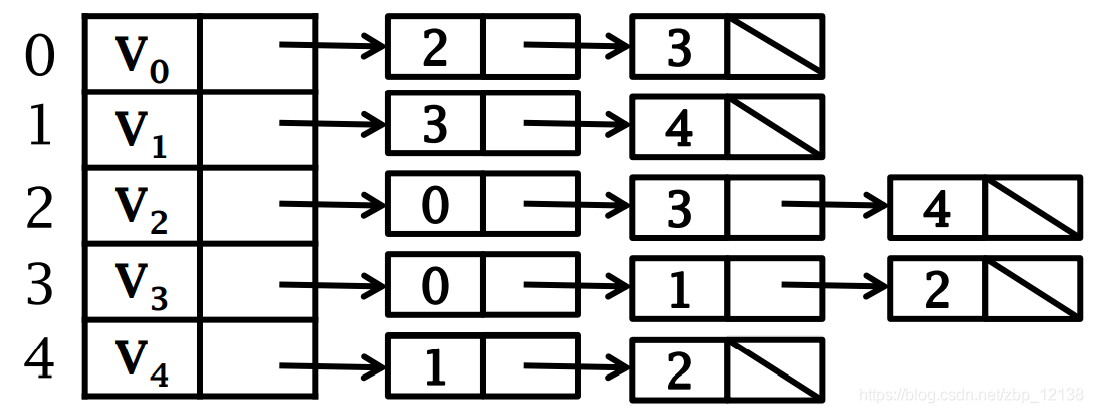
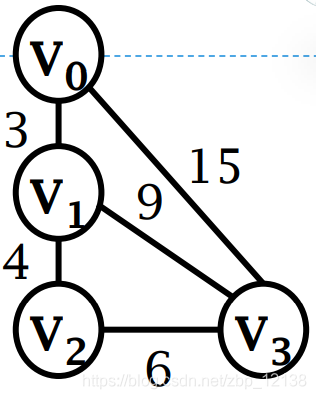
Представление взвешенных графов списком смежности

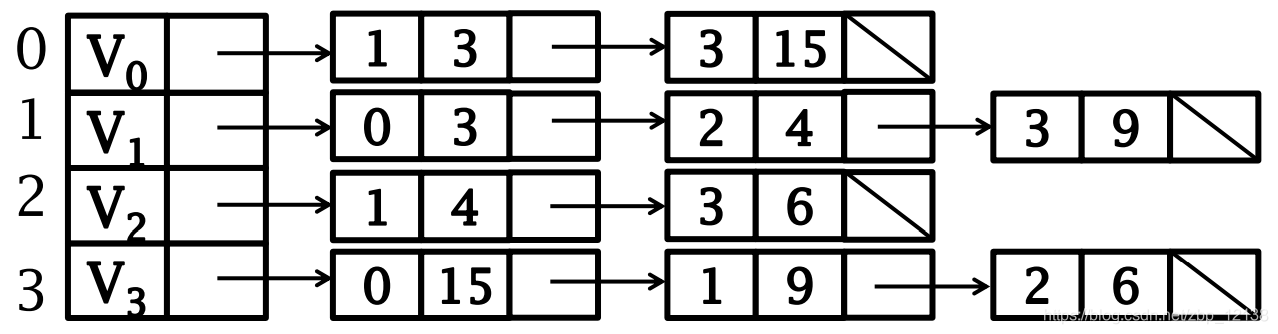
ориентированный графизсписок смежности（внесторонаповерхность）

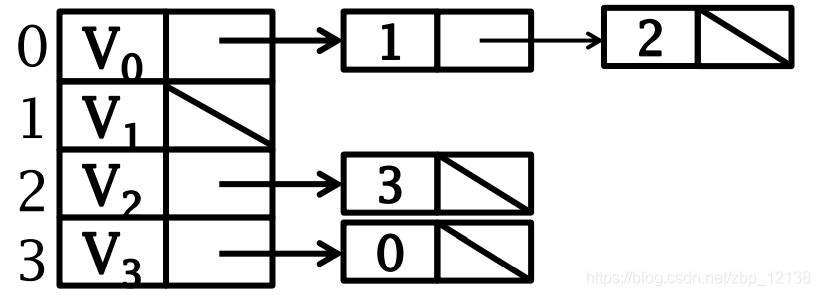
ориентированный графизобеспечить регресссписок смежности（входитьсторонаповерхность）

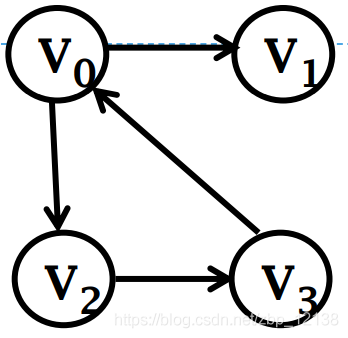
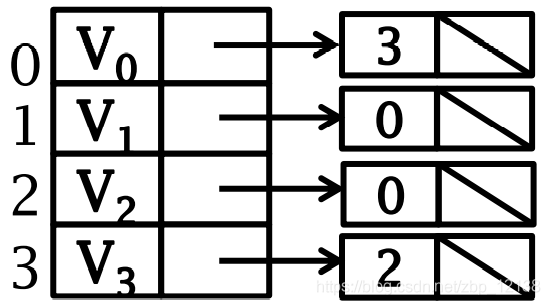
1.2.3 Ортогональный список

Его можно рассматривать как комбинацию списка смежности и обратного списка смежности.

Каждая дуга, соответствующая ориентированному графу, имеет запись, всего существует 5 доменов:

• голова
• хвост
• Следующая хвостовая дуга Tailnextarc
• главаnextarc
• Вес дуги и другие информационные поля

Запись вершины состоит из 3 полей:

• область данных
• firstinarc Первая дуга, заканчивающаяся в этой вершине.
• firstoutarc Первая дуга, начинающаяся из этой вершины.

Перекрёстный список состоит из двух наборов связанных списков:

• Последовательность указателей на строки и столбцы Каждый узел содержит два указателя:
• Преемник той же линии
• Преемник той же колонки

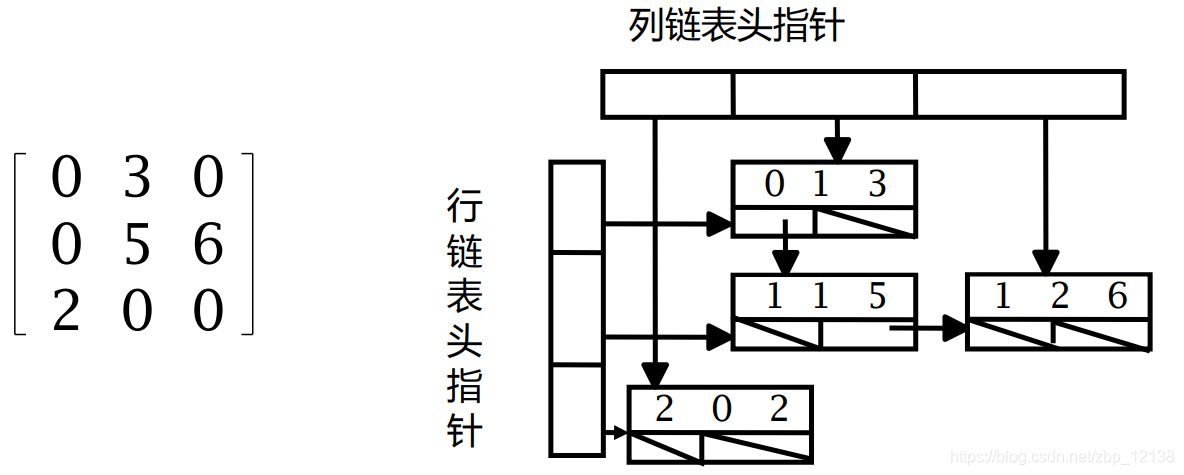
Эти три метода представления эквивалентны, и мы можем выбрать метод хранения графа в соответствии со сценарием использования.

1.3 Краткое пояснение типов и свойств графиков

Графы можно классифицировать по разным стандартам. Здесь мы в основном говорим об одном методе классификации — изоморфных графах и гетерогенных графах.

Изоморфные графы и гетерогенные графы

1. Изоморфизм изображение: Существует только один тип узла типа исторона изображения.
2. Неоднородное изображение: тип узел + тип стороны> 2 картина.

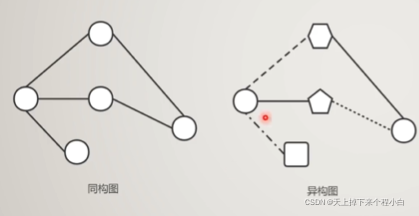
Два графа G и H являются изоморфными графами, и граф H может быть создан путем перемаркировки вершин графа G.

Если G и H изоморфны, то их порядок одинаков, размер одинаков и степени их вершин тоже одинаковы.

Гетерогенный граф — это новая концепция, соответствующая изоморфному графу.

В традиционных однородных данных графа существует только один тип узла и ребра. Поэтому при построении нейронной сети графа все узлы имеют одинаковые параметры модели и одинаковую размерность пространства признаков.

В гетерогенном графе может быть несколько типов узлов и ребер, что позволяет различным типам узлов иметь характеристики или атрибуты разных измерений.

2. Графовые алгоритмы и анализ графов

Графовая аналитика использует графический подход для анализа связанных данных. Мы можем: запрашивать данные графика, использовать базовую статистическую информацию, визуально исследовать графики, отображать графики или предварительно обрабатывать информацию графика и включать ее в задачи машинного обучения. Запросы к графам обычно используются для локального анализа данных, тогда как вычисление графа обычно включает в себя весь граф и итеративный анализ.

Графовые алгоритмы являются одним из инструментов анализа графов. Графовые алгоритмы предоставляют один из наиболее эффективных методов анализа связанных данных. Они описывают, как обрабатывать графики, чтобы сделать некоторые качественные или количественные выводы. Алгоритмы графов основаны на теории графов и используют отношения между узлами для определения структуры и изменений сложных систем. Мы можем использовать эти алгоритмы для раскрытия скрытой информации, проверки бизнес-предположений и прогнозирования поведения.

2.1 Поиск пути и поиск

Алгоритмы поиска по графу (алгоритмы поиска пути и поиска) исследуют граф для общего обнаружения или явного поиска. Эти алгоритмы работают путем поиска множества путей в графе, но не ожидают, что эти пути будут вычислительно оптимальными (например, самыми короткими или будут иметь наименьшую сумму весов). Алгоритмы поиска по графам включают поиск в ширину и поиск в глубину, которые имеют основополагающее значение для обхода графов и часто являются первым шагом во многих других типах анализа.

Алгоритмы поиска пути основаны на алгоритмах поиска графов и исследуют пути между узлами. Эти пути начинаются в узле и пересекают связи, пока не достигнут пункта назначения. Алгоритмы поиска пути определяют оптимальные пути и используются для планирования логистики, решения задач вызовов с наименьшими затратами или IP-маршрутизации, а также игрового моделирования.

Обход графа заключается в том, чтобы дать граф G и любую вершину V0 и систематически посещать все вершины в G, начиная с V0. Каждая вершина посещается только один раз.

Начиная с одной вершины, предварительно посетите остальные вершины, учитывая следующие ситуации:

• отвершина Отправляться,Может не достичь всех остальных вершин,нравиться：Нетподключенкартина；
• Также возможно попасть в бесконечный цикл, например:

Обычно для каждой вершины можно зарезервировать бит метки:

• В начале алгоритма положение флагов всех вершин равно нулю.
• В процессе обхода при посещении вершины ее Флаговый бит помечен как посещенный

2.1.1глубокийстепень Сначала пройдите&широкийстепень Сначала пройдите|DFS & BFS

Два самых основных алгоритма обхода в графовых алгоритмах: поиск в ширину (BFS) и поиск в глубину (DFS). Начиная с выбранного узла, BFS сначала обращается ко всем узлам со связями первой степени, а затем продолжает посещать узлы со связями второй степени и так далее. DFS начинается с выбранного узла. После выбора любого соседа он проходит максимально возможное расстояние вдоль края, а затем возвращается назад, зная, что не может двигаться вперед.

Поиск в глубину (сокращенно DFS) аналогичен обходу дерева по корню: если возможно, сначала выполняется поиск в направлении глубины:

1. Выберите непосещенную точку v0 в качестве исходной точки.
2. Посетите вершину v0
3. Рекурсивно глубокий поиск v0 соседствоприезжатьиз其他顶点
4. 重复上述过程Пока от v0 Все вершины, достижимые по пути, посещены.
5. Затем выберите другой безымянный вершинкак выполнить глубокий поиск по исходной точке, и все вершины приезжатькартина были посещены

[Не удалось передать изображение по внешней ссылке. Исходный сайт может иметь механизм защиты от кражи. Рекомендуется сохранить изображение и загрузить его напрямую (img-TIjFNLZu-1667871466130) (https://s2.51cto.com/images/). блог/202211/08091945_6369aeb1b5ead90326.pn g?x-oss-process=image/watermark,size_14,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_100,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=)]

Порядок поиска в глубину следующий: a->b->c->f->d->e->g

Поиск в ширину

Поиск в ширину (BFS). Процесс обхода:

1. Определенная вершина в откартине v0 Отправляться
2. После посещения и пометки вершины v0
3. Поиск всех соседних точек v0 по горизонтали, слой за слоем.
4. Ищите эти соседние точки горизонтально слой за слоем, пока все v0 Все вершины, достижимые по пути, посещены.
5. Затем выберите другой безымянный вершина Исходная точка широко разыскивается, и все точки в непосредственной близости посещены

Порядок поиска в ширину следующий: a->b->d->e->f->c->g

2.1.2 Кратчайший путь

Алгоритм кратчайших путей вычисляет кратчайший путь (минимальная сумма весов) между заданными двумя узлами. Алгоритм может взаимодействовать и выдавать результаты в режиме реального времени, может определять степень распространения отношений, может быстро определять кратчайшее расстояние между двумя точками, может рассчитывать маршрут с наименьшей стоимостью между двумя точками и так далее. Например:

• Навигация: Google, Байстепень и Гаодеди предоставляют функции навигации и используют алгоритм пути (или очень близкий вариант);
• социальная сетьсвязь：когда мысуществовать При просмотре чьего-либо профиля на социальных платформах, таких как LinkedIn и Renren (с указанием возраста), платформа покажет, сколько у вас общих друзей, и перечислит отношения между вами.

2.1.2.1 Кратчайшие пути с одним источником -------алгоритм Дейкстры

Кратчайший путь из одного источника представляет собой заданный взвешенный граф. G = <V,E>,вкаждыйсторона (vi,vj) Право на W[vi, vj] это неотрицательные действительные числа . Вычисляет заданную исходную точку из любой s Кратчайший путь ко всем остальным узлам

Алгоритм Дейкстры

Самый распространенный алгоритм кратчайшего пути был предложен Эдсгером Дейкстрой в 1956 году. Алгоритм Дейкстры сначала выбирает узел с наименьшим весом, соединенный с начальной точкой, которая является «ближайшим» узлом, а затем сравнивает вес начальной точки со вторым ближайшим узлом с совокупной суммой весов следующего ближайшего узла с ближайший соседний узел, чтобы определить, как идти дальше. Можно представить, что совокупная сумма весов, записанная алгоритмом, подобна географической «контурной линии», распространяющейся в виде «волн» на графике до тех пор, пока не достигнет узла назначения.

Основная идея

Разделите все узлы на две группы:

• В первую группу U входят узлы, для которых определен кратчайший путь.
• Во вторую группу В–У входят узлы, для которых еще не определен кратчайший путь.

Добавьте узлы второй группы в первую группу один за другим в порядке увеличения длины кратчайшего пути:

• Пока от s Отправлять доступные узлы включены в первую группасередина

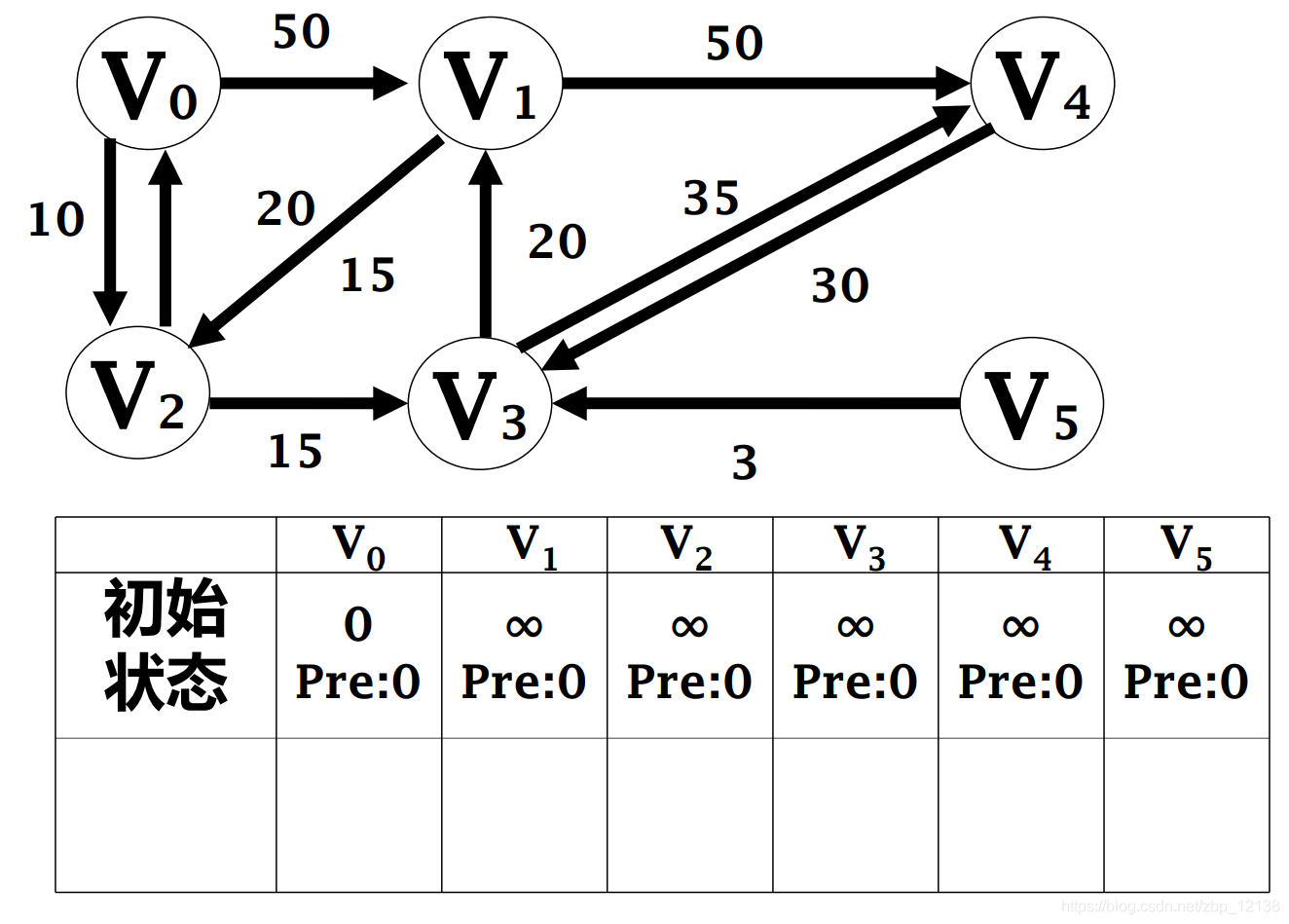
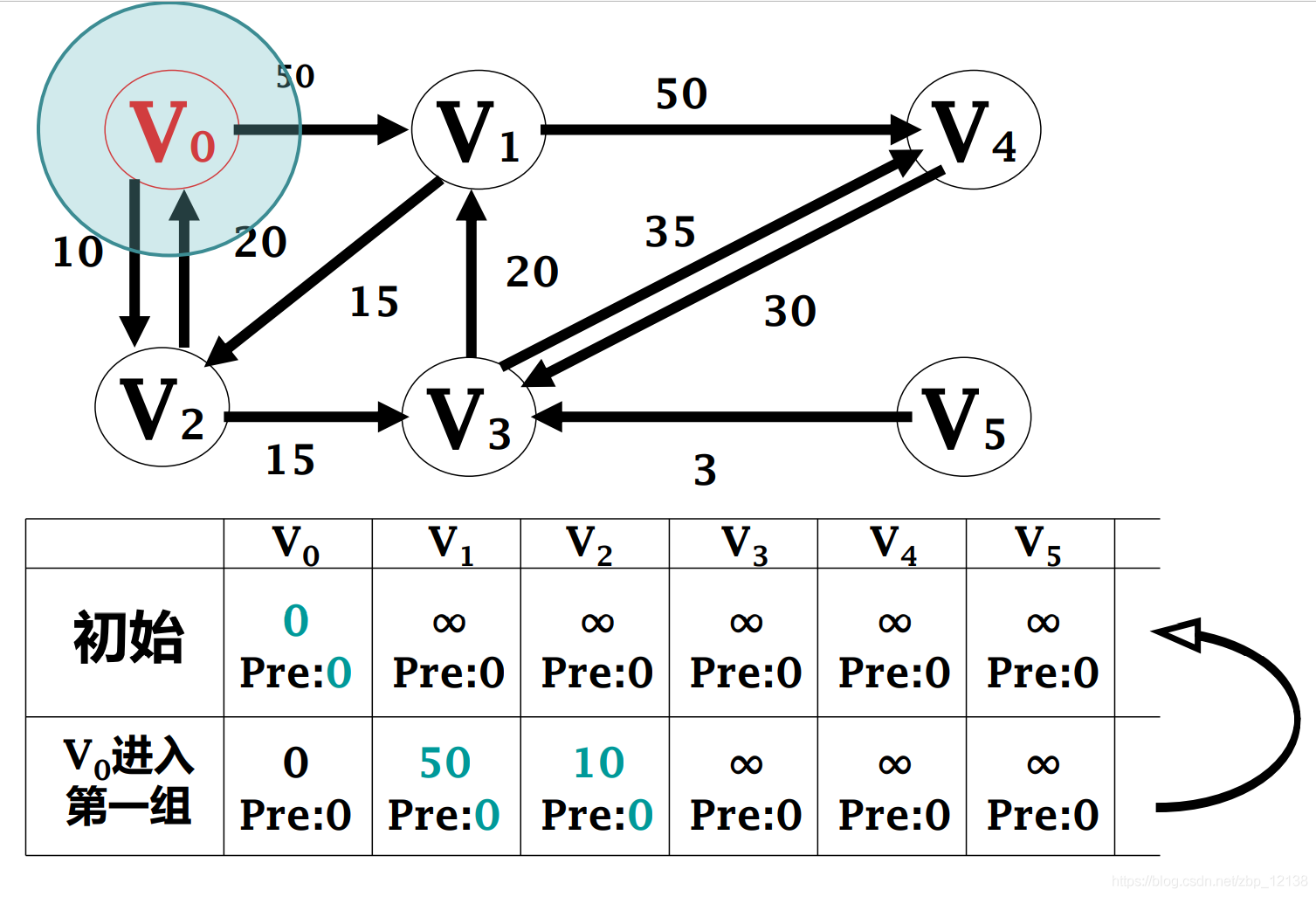
[Не удалось передать изображение по внешней ссылке. Исходный сайт может иметь механизм защиты от кражи. Рекомендуется сохранить изображение и загрузить его напрямую (img-74P2gj2A-1667871466131) (https://s2.51cto.com/images/). блог/202211/08092005_6369aec5eeea56703.pn g?x-oss-process=image/watermark,size_14,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_100,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=)]

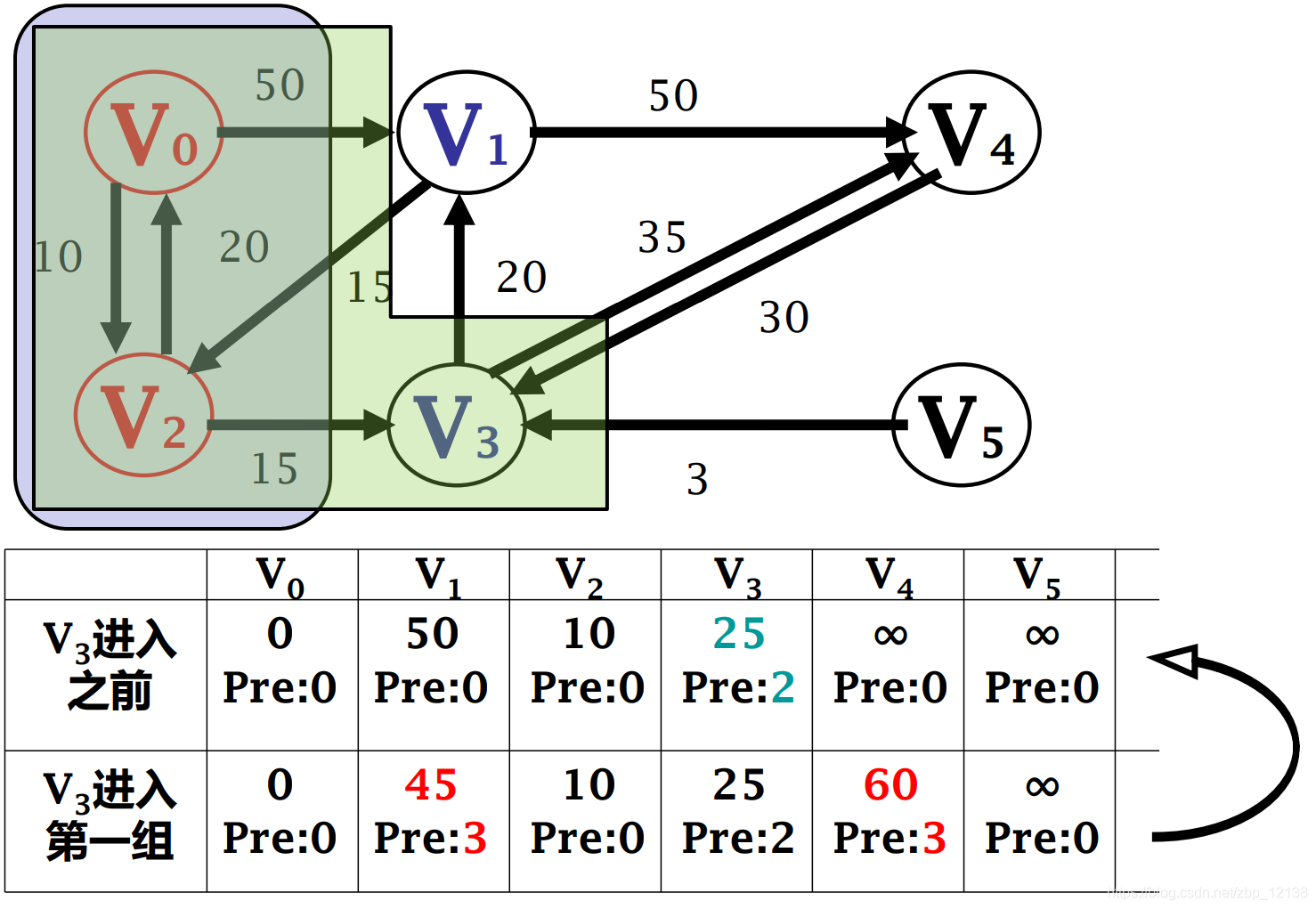
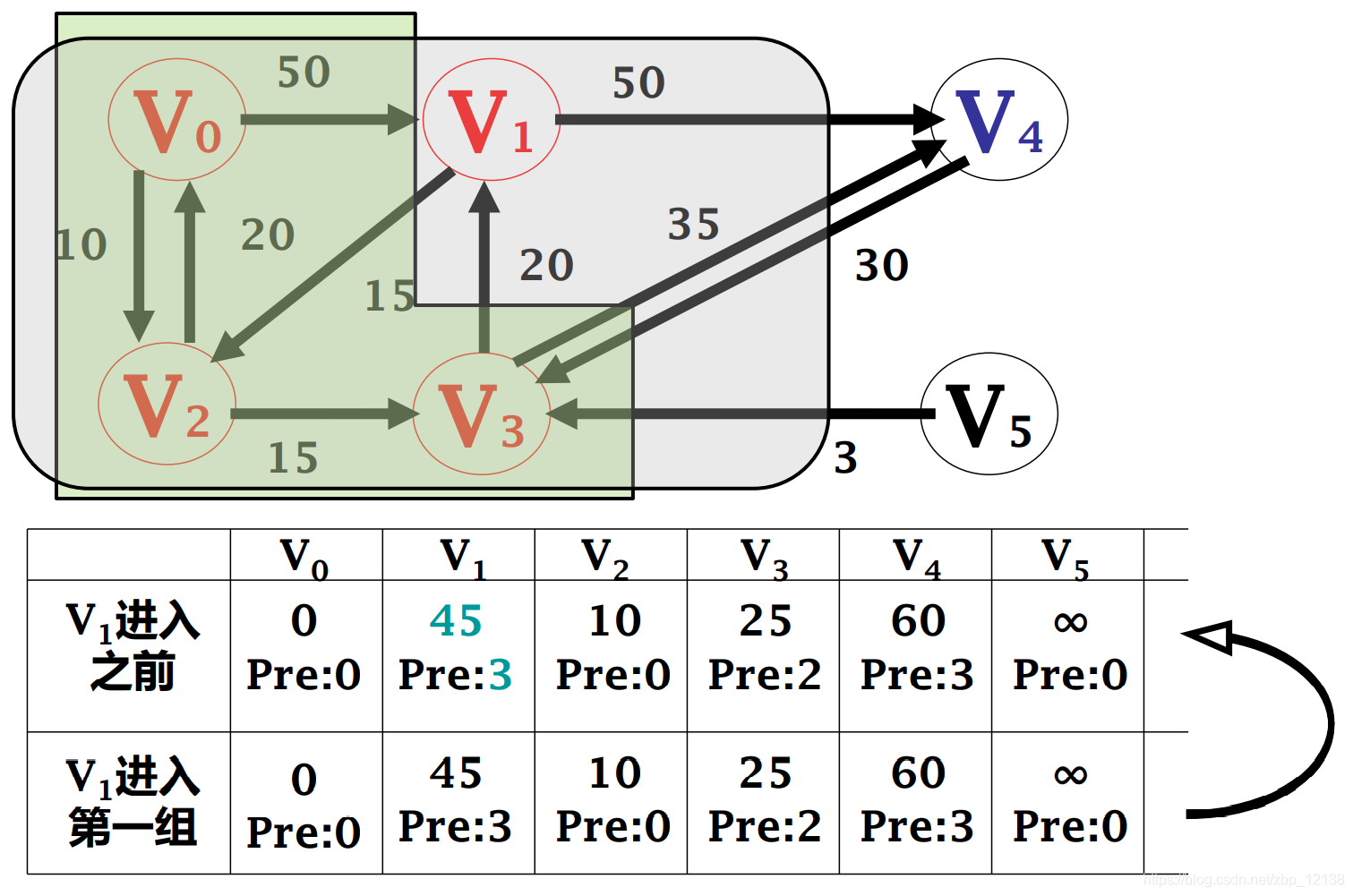
Прочитав вышеизложенное, посмотрите на это, чтобы судить, полностью ли вы это понимаете:

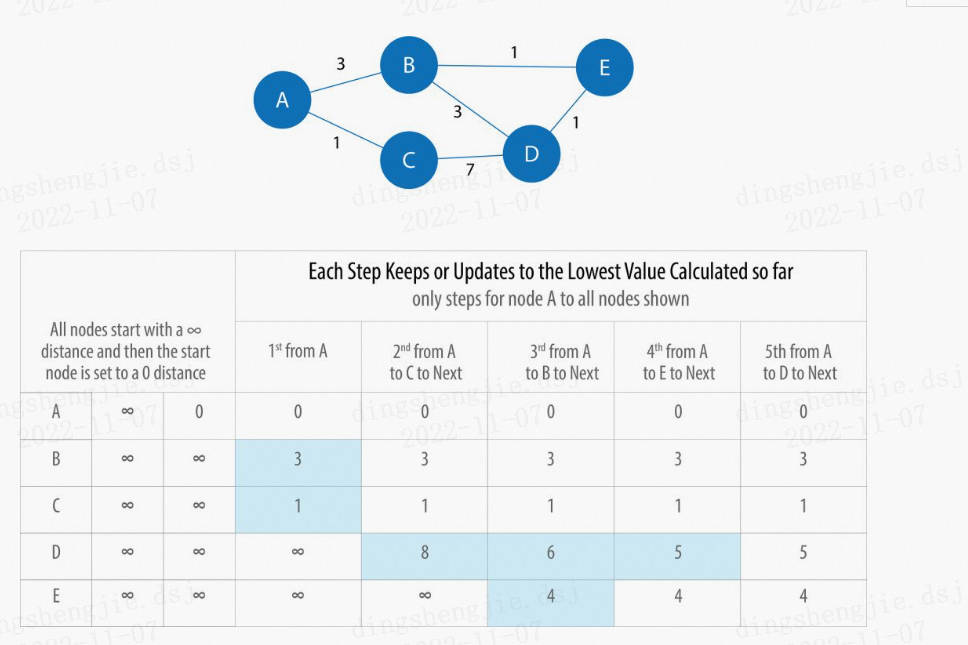
Алгоритм Дейкстры является жадным методом и не подходит для отрицательных весов. Потому что после того, как вес будет принят как минимум, он не вернется и не будет пересчитан. Даже если отрицательного цикла нет, позже могут появиться отрицательные веса, что приведет к общим ошибкам расчета.

2.1.2.2 Кратчайший путь между каждой парой узлов

Алгоритм Флойда находит кратчайший путь между каждой парой узлов.

Использовать матрицу смежности adj Приходитьповерхностьправо демонстрироватьориентированный граф

Основная идея

• Инициализировать adj(0) для соседней матрицы adj
• существоватьматрица Сделай это на adj(0) n итераций, рекурсивно генерируют матричную последовательность adj(1),…,adj(k),…,adj(n)
• Среди них после k-й итерации adj(k)[i,j] Значение узла vi приезжатьузел vj Номера узлов, передаваемых по пути,не превышают k изкратчайший путьдлинныйстепень

Основная идея – метод динамического программирования.

Существует два широко используемых варианта алгоритма кратчайшего пути: алгоритм A (можно произносить как звезда) и K-кратчайшие пути Йены. Алгоритм оптимизирует направление следующего исследования алгоритма, предоставляя дополнительную информацию. K-Shortest Paths Йены не только дает результаты по кратчайшим путям, но также дает лучшие K путей.

Все узлы соединяют кратчайший путь (Все Pairs Shortest Path）такжеэто Обычно используетсяизкратчайший Алгоритм пути, вычисляет кратчайший из всех пар узлов путь. Сравните вызовы одного кратчайшего по одному алгоритм пути, Все Pairs Shortest Path Алгоритм будет быстрее. Алгоритм параллельно вычисляет информацию из нескольких узлов, и эту информацию можно повторно использовать в вычислениях.

2.1.3 Минимальное связующее дерево

Алгоритм минимального связующего дерева начинается с заданного узла, находит все его достижимые узлы и соединяет узлы с наименьшим возможным весом, чтобы сформировать набор отношений. Он проходит от посещенного узла к следующему непосещенному узлу с минимальным весом, избегая циклов.

Наиболее часто используемый алгоритм минимального связующего дерева основан на алгоритме Прима, разработанном в 1957 году. Алгоритм Прима аналогичен кратчайшему пути Дейкстры. Разница в том, что алгоритм Прима каждый раз ищет минимальный вес для посещения следующего узла, а не накапливает сумму весов. Кроме того, алгоритм Прима допускает отрицательные веса ребер.

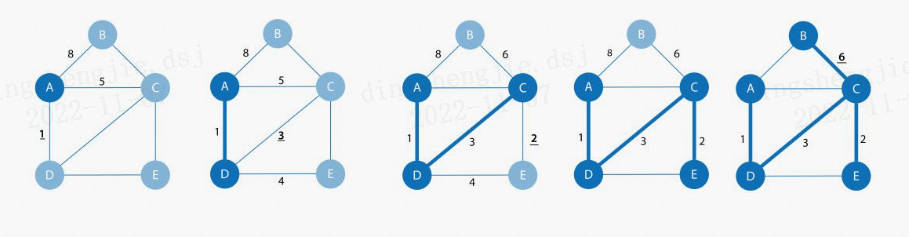
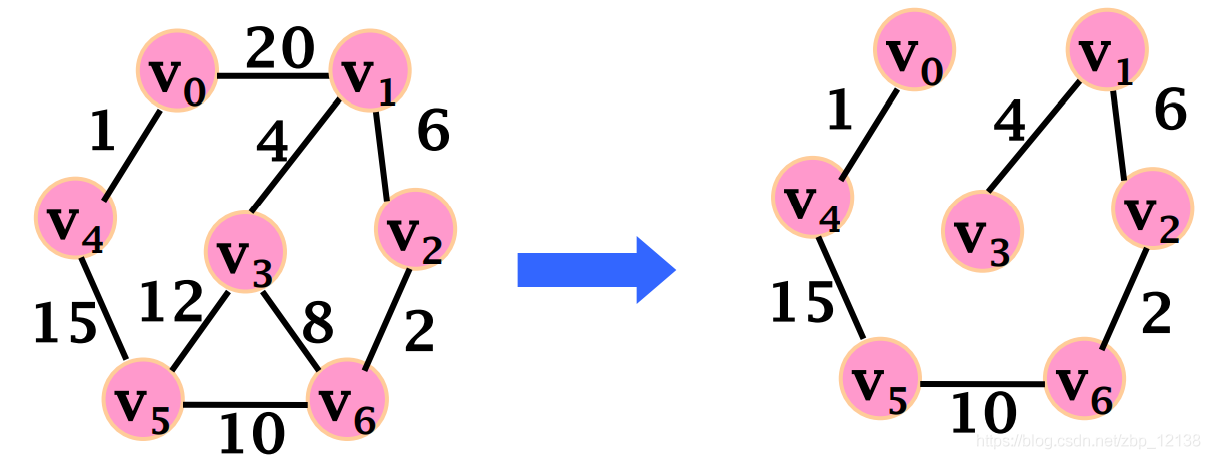
На рисунке выше представлена ​​пошаговая декомпозиция алгоритма минимального остовного дерева. Алгоритм в конечном итоге обходит граф с наименьшим весом, и в процессе обхода цикл не генерируется.

Алгоритмы можно использовать для оптимизации путей, соединяющих системы, такие как водопроводные трубы и схемы. Он также используется для аппроксимации некоторых задач, время вычисления которых неизвестно, например, задачи коммивояжера. Хотя этот алгоритм не всегда может найти абсолютно оптимальное решение, он делает гораздо более возможным чрезвычайно сложный и трудоемкий анализ. Например:

• Планирование путешествий: сведите к минимуму расходы на путешествие по стране;
• Отслеживание истории передачи гриппа: молекулярно-эпидемиологическое расследование госпитальной вспышки инфекции вируса гепатита С с использованием модели минимального связующего дерева

2.1.4 Случайное блуждание

Случайное блуждание Walk) алгоритм для получения случайного пути. случайное блужданиеалгоритмотодинузелначинать,Случайным образом искать приезжать к своим соседям по стороне вперед или назад.,и так далее,Путь от места жительства к месту проживания проложен длинными степенями. Этот процесс немного похож на пьяное существование, блуждание по городу.,Вероятно, он примерно знает, куда идет.,Но путь может быть крайне извилистым,после всего,Он тоже не может себя контролировать~

Алгоритм случайного блуждания обычно используется для случайной генерации набора связанных данных узла для последующей обработки данных или других алгоритмов. Например:

• как node2vec и graph2vec часть алгоритмов, которые можно использовать для генерации узловых векторов, а также для последующих входных данных глубокого уровня для обучения. Это важно понимать; NLP (Обработка естественного языка) Друзьям несложно понять. Слова являются частью предложений, и мы можем обучать векторы слов с помощью словосочетаний (корпуса). Затем мы также можем использовать комбинацию узла (Random Walk) для обучения вектора узла. Эти векторы могут представлять значение слов или узлов и могут быть рассчитаны численно. Применение этой области очень интересно, и мы будем искать возможности представить ее подробно;
• как Walktrap и Infomap Часть алгоритма открытия сообщества. Если случайное блуждание всегда возвращает одну и ту же группу узлов, указывая, что эти узлы могут принадлежать одному и тому же сообществу;
• Часть другой модели машинного обучения, используемой для случайной генерации связанных данных узеля.

2.2 Вычисление центральности

Алгоритмы центральности используются для определения роли конкретных узлов в графе и их влияния на сеть. Алгоритмы централизации могут помочь нам определить наиболее важные узлы и понять групповую динамику, такую ​​как надежность, доступность, скорость распространения событий и связи между группами. Хотя многие из этих алгоритмов были изобретены для анализа социальных сетей, они нашли применение во многих отраслях и областях.

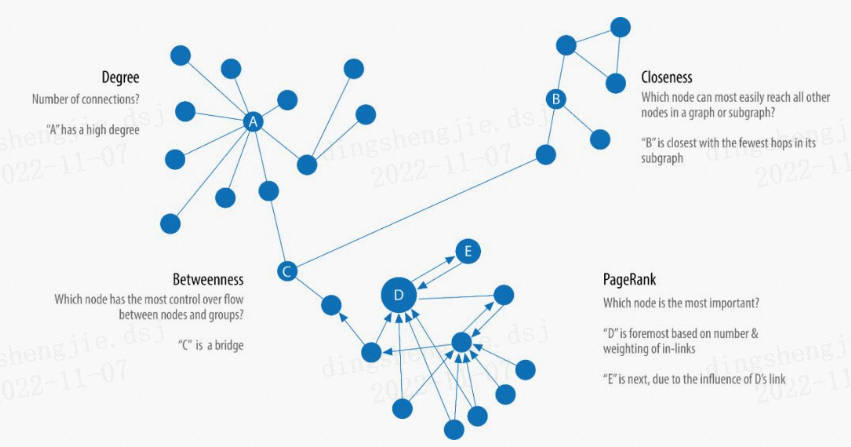
2.2.1 DegreeCentrality

Degree Centrality (степень центральности, индикатор центральности, основанный на степени), вероятно, самый простой «алгоритм» во всем посте блога. Степень подсчитывает количество ребер, напрямую соединенных с узлом, включая исходящую и входную степень. Степень можно просто понимать как размер возможности доступа узла. Например, в социальной сети человек (узел) с большим количеством степеней с большей вероятностью будет иметь прямой контакт с людьми и с большей вероятностью заболеет гриппом.

Средняя степень сети — это количество ребер, деленное на количество узлов. Конечно, средняя степень может быть легко «искажена» некоторыми узлами с чрезвычайно большими степенями. Следовательно, распределение степеней может быть лучшим индикатором характеристик сети.

Если вы хотите оценить центральность узла по исходящей и входящей степени, вы можете использовать степень центральности. Степень централизации хорошо работает, когда основное внимание уделяется прямым связям. Сценарии применения включают в себя различение законных пользователей онлайн-аукционов от мошенников. Мошенники имеют более высокий вес из-за искусственно завышенных аукционных цен.

2.2.2 ClosenessCentrality

Центральность по близости — это метод обнаружения узлов, которые эффективно распространяют информацию через подграф. Центральность близости измеряет близость (обратную расстоянию) узла ко всем другим узлам. Узел с высокой степенью близости имеет наименьшее расстояние ко всем другим узлам.

Для узла центральность близости является обратной суммой минимальных расстояний от узла до всех остальных узлов:

где u — узел, для которого мы хотим вычислить центральность близости, n — общее количество узлов в сети, а d(u,v) представляет собой кратчайшее расстояние пути между узлом u и узлом v. Более часто используемая формула — это нормализованная центральность, которая вычисляет величину, обратную среднему расстоянию от узла до других узлов. Знаете ли вы, как изменить приведенную выше формулу? Кстати, просто замените 1 в числителе на n-1.

Поняв формулу, мы найдем,нравитьсяфруктыкартинаэто Нетподключенкартина,Тогда мы не сможем вычислить центральность по близости. Итак, для неподключеннойкартины,настраиватьисерединахарактер（Harmonic была предложена центральность) (конечно, у нее есть и нормализованная версия, угадайте, куда на этот раз нужно добавить n-1?):

Вассерман и Фауст предложили другую формулу для расчета центральности близости, которая специально используется для несвязных графов, содержащих несколько подграфов и не связанных между собой:

Среди них Н. — общее количество узлов в графе, n эточасть（component）серединаизузелколичество。

Когда мы хотим сосредоточиться на узлах сети, которые распространяют информацию быстрее всего, мы можем использовать центральность по близости.

2.2.3 BetweennessCentrality

Центральность по посредничеству — это метод определения степени влияния узлов на поток информации или ресурсов в графе. Его часто используют для поиска узлов моста, соединяющих две части графа. Потому что во многих случаях наиболее важными «механиками» системы являются не те, которые находятся в лучшем состоянии, а какие-то, казалось бы, незаметные «носители», которые контролируют поток ресурсов или информации.

Алгоритм централизации по посредничеству сначала вычисляет кратчайший (минимальная сумма весов) путь, соединяющий каждую пару узлов в графе. Каждый узел получает оценку, основанную на количестве кратчайших путей через узел. Чем короче путь, по которому находится узел, тем выше его оценка. Формула расчета:

Среди них p — количество кратчайших путей между узлами s и t, а p(u) — количество путей, проходящих через узел u. На следующем рисунке показан процесс расчета для узла D:

Конечно, вычисление централизации по посредничеству на большом графе обходится очень дорого. Поэтому для вычислений нам нужны более быстрые, менее дорогие и примерно такие же по точности алгоритмы, такие как рандомизированно-аппроксимированный алгоритм Брандеса. Мы не будем углубляться в этот алгоритм. Если вам интересно, вы можете узнать, как алгоритм достигает приблизительных результатов посредством случайности (Random) и отбора степеней (Degree).

Центральность посредничества имеет широкий спектр применений в реальных сетях, где мы используем ее для обнаружения узких мест, контрольных точек и уязвимостей. Например, выявление влиятельных лиц из разных организаций, которые часто являются посредниками для каждой организации, например, поиск ключевых точек в энергосистеме для повышения общей надежности.

2.2.4 PageRank

Среди всех алгоритмов централизации PageRank является самым известным. Он измеряет способность узла оказывать влияние. PageRank учитывает не только прямое влияние узлов, но и влияние «соседей». Например, узел с одним влиятельным «сосеем» может быть более влиятельным, чем узел с множеством менее влиятельных «соседей». PageRank подсчитывает количество и качество входящих связей с узлом, тем самым определяя важность узла.

Алгоритм PageRank назван в честь соучредителя Google Ларри Пейджа, который создал алгоритм для ранжирования веб-сайтов в результатах поиска Google. Различные веб-страницы ссылаются друг на друга, веб-страницы используются как узлы, а ссылочные отношения используются как ребра для формирования сети. Веб-страницы, которые цитируются большим количеством веб-страниц, должны иметь более высокий вес; веб-страницы, цитируемые более высокими весами, также должны иметь более высокий вес. Исходная формула:

где u — веб-страница, для которой мы хотим рассчитать PageRank, а от T1 до Tn — ссылающиеся веб-страницы. d называется коэффициентом демпфирования, который представляет вероятность того, что пользователь продолжит нажимать на веб-страницу. Обычно он равен 0,85 в диапазоне от 0 до 1. C(T) — исходящая степень узла T.

С точки зрения понимания, алгоритм PageRank предполагает, что когда пользователь посещает веб-страницу, он может случайным образом ввести URL-адрес или может получить доступ к другим веб-страницам через ссылки на некоторые веб-страницы. Тогда коэффициент демпфирования представляет вероятность того, что пользователю наскучила текущая веб-страница, и он случайно выберет ссылку для посещения новой веб-страницы. Тогда значение PageRank представляет собой вероятность того, что на эту веб-страницу ссылаются другие веб-страницы (в определенной степени). Итак, как вы можете объяснить 1-d в уравнении PageRank? Фактически, 1-d представляет собой вероятность доступа к веб-странице путем случайного ввода URL-адреса вместо доступа к ней по ссылке.

Алгоритм PageRank рассчитывается итеративно до тех пор, пока результаты не сойдутся или не будет достигнут верхний предел итерации. На каждой итерации веса узлов и веса ребер будут обновляться в два этапа, как показано на рисунке ниже:

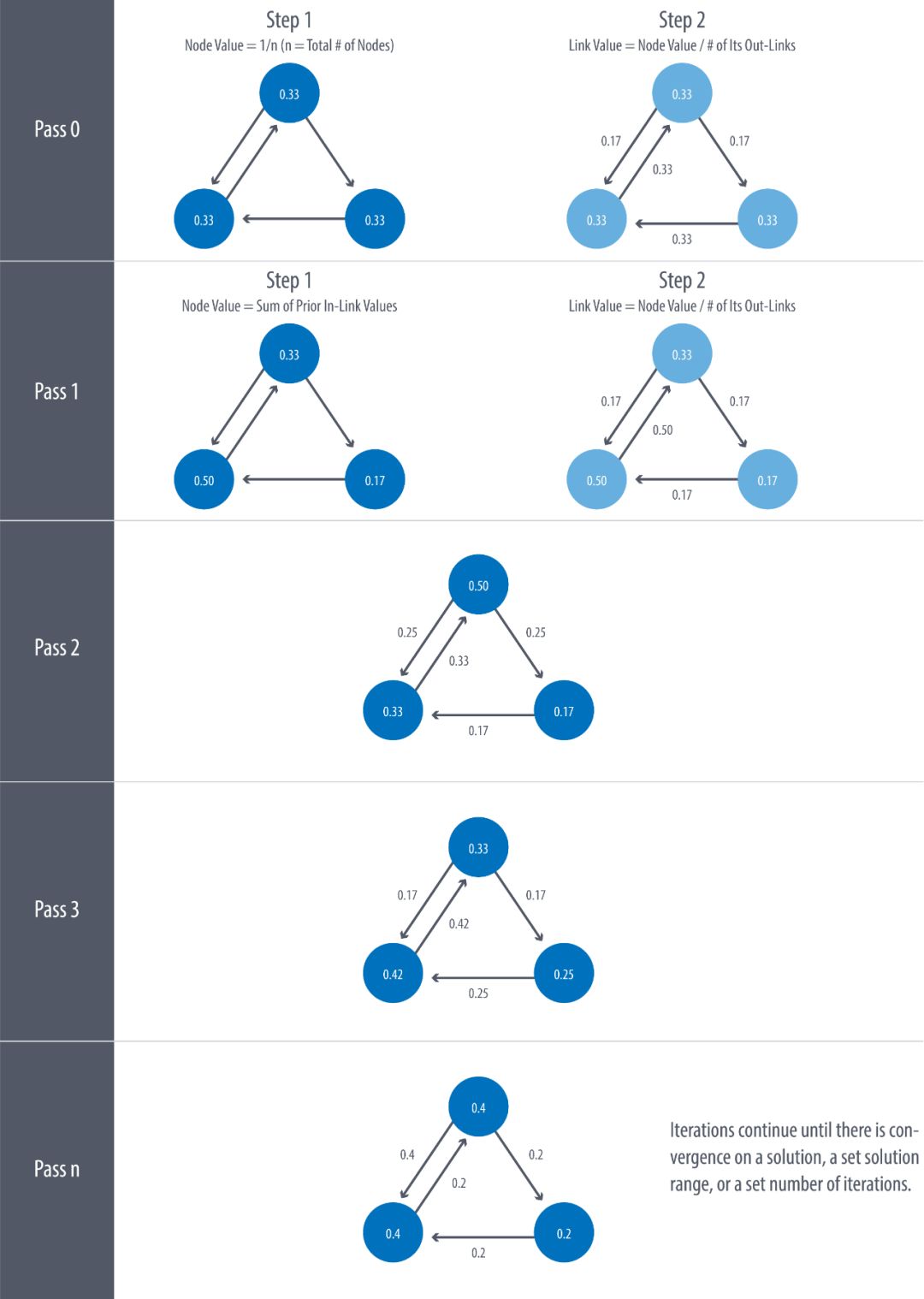
Конечно, расчет на приведенном выше рисунке не учитывает коэффициент демпфирования, так зачем же коэффициент демпфирования необходим? Помимо определяемой нами вероятности доступа по ссылке, есть ли еще какой-то смысл? Из процесса, показанного на рисунке выше, мы можем обнаружить проблему. Что произойдет, если в узел (или группу узлов) есть только входящие ребра, но нет выходящих ребер? Согласно итерации, показанной на рисунке выше, узлы будут продолжать получать баллы PageRank. Это явление называется Rank Sink, как показано ниже:

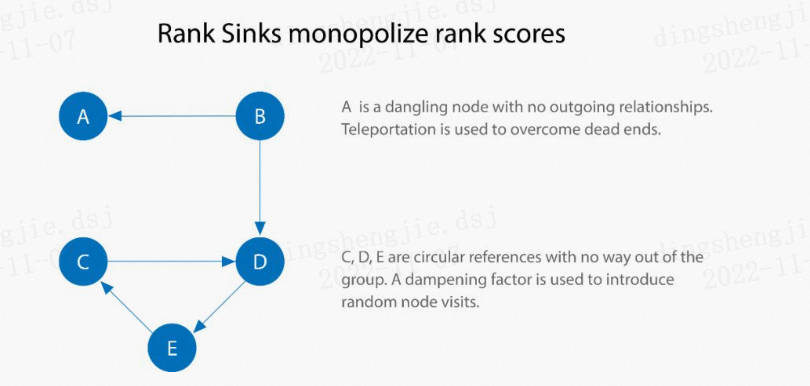
Есть два способа решить проблему Rank Sink. Во-первых, если предположить, что эти узлы имеют невидимые ребра, соединяющие все узлы, процесс прохождения этих невидимых ребер называется телепортацией. Во-вторых, используя коэффициент демпфирования, если мы установим d равным 0,85, у нас все равно будет вероятность выскока из этих узлов 0,15.

Хотя рекомендуемое значение коэффициента демпфирования составляет 0,85, мы все равно можем изменить его в соответствии с фактическими потребностями. Понижение коэффициента демпфирования означает, что при доступе к веб-странице вероятность продолжения нажатия на ссылки снижается, но происходит более случайный доступ к другим веб-страницам. Тогда показатель PageRank веб-страницы будет больше присваиваться ее непосредственным нижестоящим веб-страницам, а не нижестоящим веб-страницам.

Алгоритм PageRank больше не ограничивается рейтингом страниц. Например:

• Поиск наиболее важных генов. Гены, которые мы ищем, могут быть не генами, наиболее тесно связанными с биологическими функциями, а генами, тесно связанными с наиболее важными функциями;
• who to follow service at Twitter: Twitter использует персонализированный PageRank Алгоритм (Персонализированный PageRank, короче PPR) рекомендует пользователям, которым они, возможно, пожелают обратить внимание другие аккаунты на. Этот алгоритм объединяет интересы и другие отношения, чтобы показать пользователям других заинтересованных пользователей;
• Прогноз транспортного потока: использование PageRank Алгоритм вычисляет вероятность того, что люди остановятся или закончат поездку на каждой улице;
• Борьба с мошенничеством: в медицинской или страховой отрасли наблюдаются ненормальные или мошеннические действия, PageRank. Его можно использовать в качестве входных данных для последующих алгоритмов машинного обучения.

2.3 Алгоритм обнаружения сообществ

Формирование сообществ характерно для всех типов сетей. Выявление сообществ имеет решающее значение для оценки группового поведения или чрезвычайных ситуаций. Для сообщества внутренние узлы имеют больше связей (ребер) с внутренними узлами, чем узлы вне сообщества. Идентификация этих сообществ может выявить кластеризацию узлов, найти изолированные сообщества и выявить общие структурные связи сети. Алгоритмы обнаружения сообществ помогают обнаружить групповое поведение или предпочтения в сообществе, найти вложенные связи или стать предпосылкой для других анализов. Алгоритмы обнаружения сообщества также часто используются в сетевой визуализации.

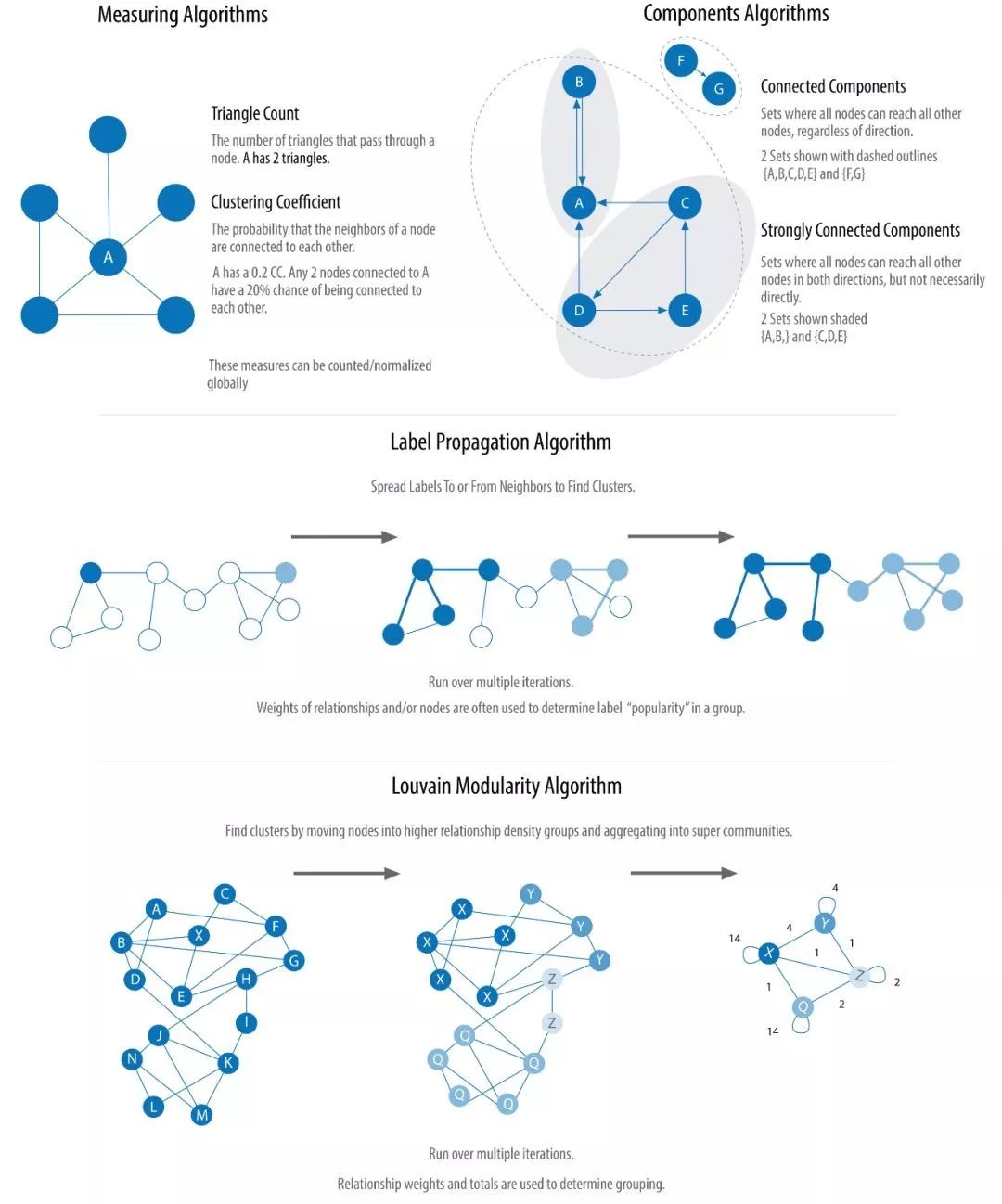
2.3.1 MeasuringAlgorithm

Число треугольников и коэффициент кластеризации часто используются вместе. Подсчет треугольников подсчитывает количество треугольников, состоящих из узлов в графе, требуя, чтобы любые два узла были соединены ребром (отношениями). Цель алгоритма коэффициента кластеризации — измерить, насколько тесно группа кластеризована. Алгоритм вычисляет количество треугольников в сети как отношение к возможным связям. Коэффициент кластеризации, равный 1, означает, что любые два узла в этой группе соединены ребром.

Существует два типа коэффициентов кластеризации: локальный коэффициент кластеризации и глобальный коэффициент кластеризации.

Коэффициент локальной кластеризации вычисляет близость между соседями узла и требует для расчета подсчета треугольников. Формула расчета:

Среди них u представляет узел, для которого нам нужно вычислить коэффициент кластеризации, R (u) представляет количество треугольников, проходящих через узел u и его соседей, а k (u) представляет степень узла u. На рисунке ниже представлена ​​схема расчета коэффициента кластеризации треугольного счета:

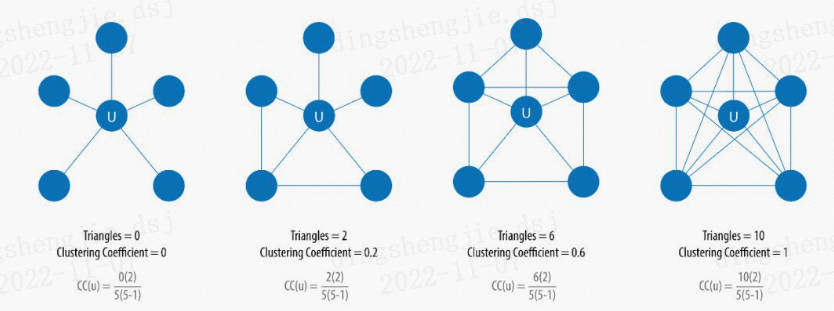
Коэффициент глобальной кластеризации представляет собой нормализованную сумму коэффициентов локальной кластеризации.

Когда нам нужно рассчитать устойчивость или коэффициент кластеризации группы, мы можем использовать подсчет треугольников. Подсчет треугольников широко используется при анализе социальных сетей, а общая навигация используется для обнаружения сообществ. Коэффициент кластеризации позволяет быстро оценить сплоченность конкретной группы или всей сети. Эти алгоритмы можно использовать вместе для поиска конкретных сетевых структур. Например, изучите тематическую структуру веб-страниц и определите «сообщества веб-страниц» с общими темами, основанными на взаимосвязях между веб-страницами.

2.3.2 ComponentsAlgorithm

Сильно связанные компоненты (Сильно связанные Connected Компоненты, аббревиатура SCC) алгоритм поиска ориентированного Группа узлов внутри графа, каждая группа узлов может быть связана друг друга доступ. существовать “Community Detection Algorithms” На диаграмме мы видим, что каждая группа узлов не нуждается в прямом внутреннем соединении, если доступ к ним осуществляется через пути.

В алгоритме связанных компонентов, в отличие от SCC, пары узлов внутри группы должны быть доступны только в одном направлении.

Ранние алгоритмы ассоциативного алгоритма анализа картины,Чтобы понять структуру изображения,Он очень эффективен при выявлении тесных групп, которые могут потребовать независимого расследования. Для таких приложений, как рекомендательные системы,Его также можно использовать для описания схожего поведения в группе и т. д. много раз,Алгоритмы используются для поиска кластеров и объединения их в один узел.,для дальнейшего межкластерного анализа. для нас,Сначала запустите следующий алгоритм корреляции, чтобы проверить, подключено ли изображение.,это Очень хорошая привычка.

2.3.3 LabelPropagation Algorithm

Алгоритм распространения меток (Label Propagation Алгоритм, короче Алгоритм быстрого обнаружения сообществ в LPA этосуществоватькартина. существовать LPA В алгоритме метка узла полностью определяется его прямыми соседями. Алгоритм хорошо подходит для полуконтролируемого обучения, где вы можете использовать уже помеченные узлы для начала процесса распространения.

LPA это Новый алгоритм, созданный Raghavan и др. 2007 предложено в этом году. Мы можем очень наглядно понять процесс распространения алгоритма. Когда метки находятся в тесно связанных областях, они распространяются очень быстро, но в редко связанных областях скорость распространения снижается. Когда узел принадлежит нескольким сообществам, алгоритм будет использовать метки и веса соседей узла для определения окончательной метки. После завершения распространения узлы с одинаковой меткой считаются принадлежащими к одной группе.

На рисунке ниже показаны два варианта алгоритма: Push и Pull. Среди них алгоритм Pull более типичен и может хорошо рассчитываться параллельно:

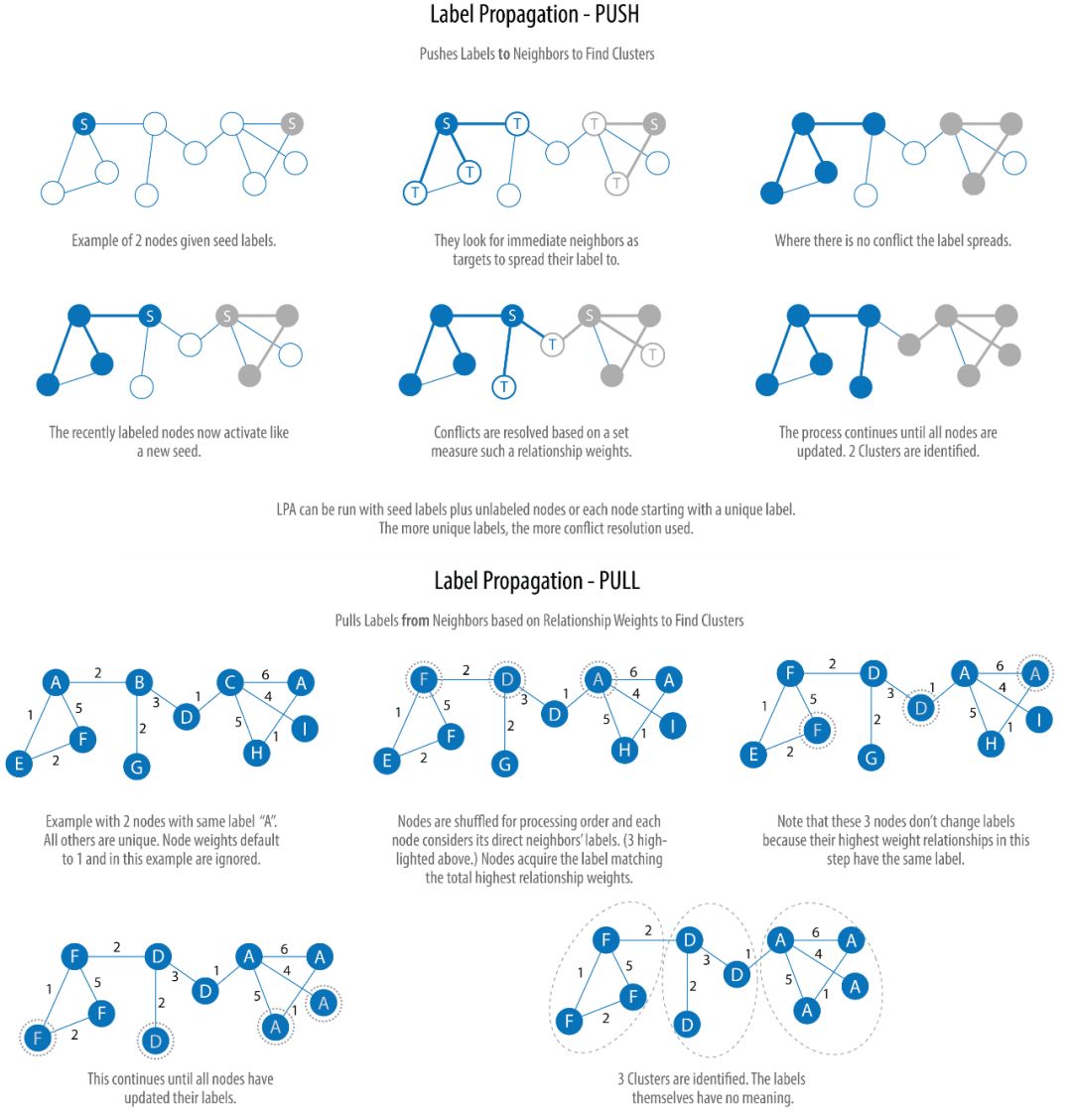
Прочитав картинку выше, вы уже должны понимать общий процесс работы алгоритма. На самом деле, люди, которые занимались обработкой изображений, легко поймут, что так называемый алгоритм распространения меток — это всего лишь вариант алгоритма сегментации изображения. Алгоритм Push — это упрощенная версия метода увеличения региона, а алгоритм Pull больше похож на него. алгоритм разделения и слияния, также известный как разделение-слияние). Действительно, пиксели изображения очень похожи на узлы графа.

2.3.4 LouvainModularity Algorithm

Когда алгоритм модульности Лувена присваивает узлу сообщество, он сравнивает плотность сообщества, а не только близость узла к сообществу. Алгоритм количественно определяет, принадлежит ли узел сообществу, сравнивая плотность отношений между узлом и сообществом со средней плотностью отношений. Алгоритм может не только обнаруживать сообщества, но также предоставлять иерархии сообществ разных масштабов и размеров, что очень помогает в понимании сетевой структуры секторов с различной степенью детализации.

После того, как алгоритм был предложен в 2008 году, он быстро стал одним из самых быстрых модульных алгоритмов. В алгоритме много деталей, и мы не можем охватить их все. На следующем рисунке показан приблизительный шаг, который поможет нам понять, как алгоритм может создавать сообщества в разных масштабах.

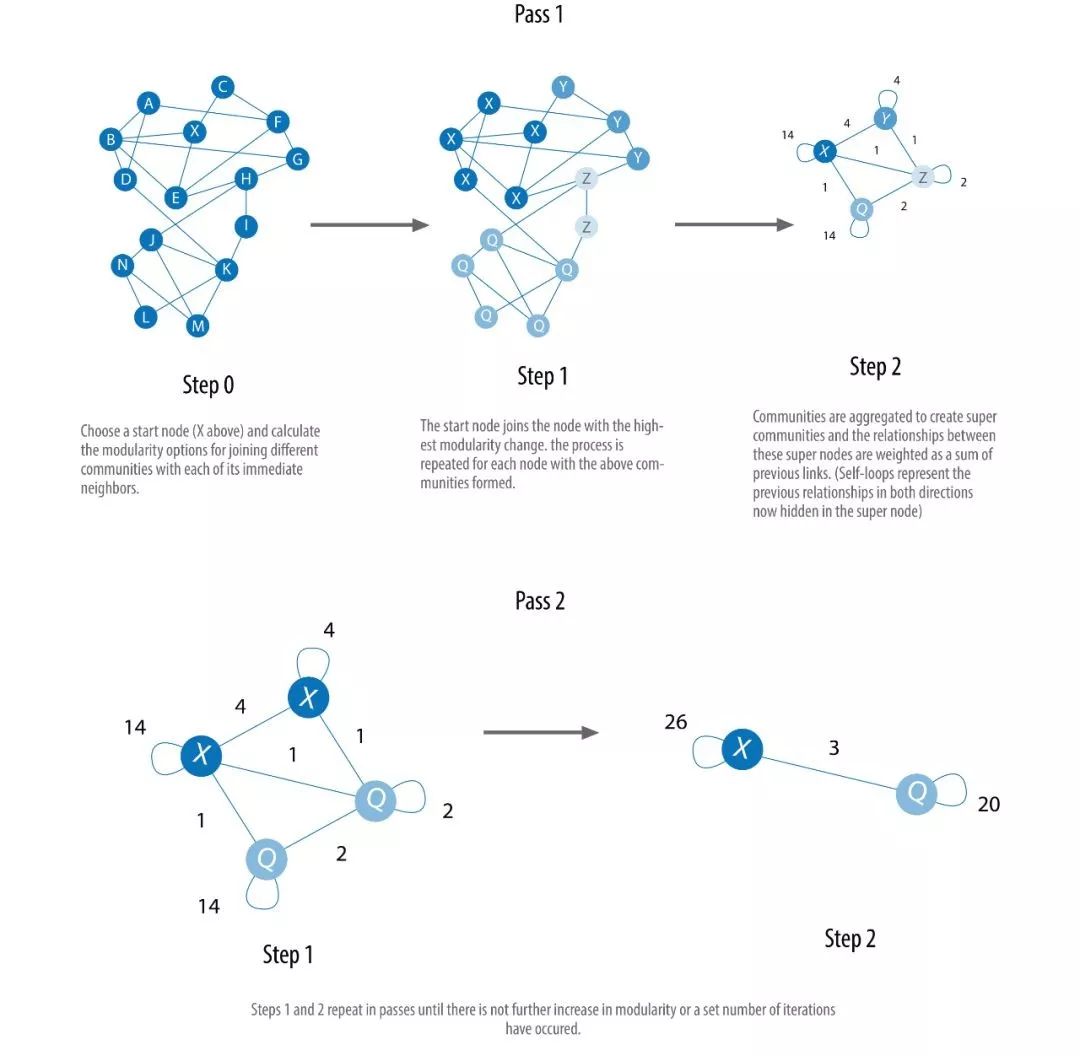
Алгоритм модульности Лувена очень подходит для обнаружения сообщества в огромных сетях. Алгоритм использует эвристический подход для преодоления ограничений традиционных алгоритмов модульности. Применение алгоритма:

• Обнаружение сетевых атак. Этот алгоритм можно применять для быстрого обнаружения сообществом проблем крупномасштабной сетевой безопасности. Как только эти сообщества будут обнаружены, их можно будет использовать для предотвращения кибератак;
• Моделирование темы: от Twitter и YouTube Извлекайте темы из социальных онлайн-платформ на основе терминов, встречающихся в документах, в рамках процесса моделирования тем.

3. Практика алгоритмов (анализ графов, расчет графов)

Имея предварительные знания, давайте вместе поработаем с программой.

3.1 Создайте график для простого анализа

import numpy as np
import random
import networkx as nx
from IPython.display import Image
import matplotlib.pyplot as plt

# Load the graph
G_karate = nx.karate_club_graph()
# Find key-values for the graph
pos = nx.spring_layout(G_karate)
# Plot the graph
nx.draw(G_karate, cmap = plt.get_cmap('rainbow'), with_labels=True, pos=pos)

Иллюстрация клуба каратэ

Что представляет собой эта диаграмма «каратэ»? Социальная сеть клуба каратэ, которую изучал Уэйн В. Захари в течение трех лет с 1970 по 1972 год. Сеть состоит из 34 членов этого клуба каратэ, а связи между парами членов указывают на то, что они связаны за пределами клуба. В ходе исследования возник конфликт между администратором JohnA и тренером Mr.Hi (псевдоним), в результате которого клуб разделился на две части. Половина участников сформировала новый клуб вокруг Mr.Hi, а другая половина нашла нового инструктора или бросила каратэ. На основании собранных данных Закари правильно отнес всех участников, кроме одного, к группе, в которую они вошли после разделения.

# .degree() Свойство возвращает список степеней (количество соседних узлов) для каждого узла данной картины:
n=34
print(G_karate.degree())
degree_sequence = list(G_karate.degree())

# Подсчитайте количество сторон, а также количество степеней последовательности:
nb_nodes = n
nb_arr = len(G_karate.edges())
avg_degree = np.mean(np.array(degree_sequence)[:,1])
med_degree = np.median(np.array(degree_sequence)[:,1])
max_degree = max(np.array(degree_sequence)[:,1])
min_degree = np.min(np.array(degree_sequence)[:,1])
# Наконец, распечатайте всю информацию:
print("Number of nodes : " + str(nb_nodes))
print("Number of edges : " + str(nb_arr))
print("Maximum degree : " + str(max_degree))
print("Minimum degree : " + str(min_degree))
print("Average degree : " + str(avg_degree))
print("Median degree : " + str(med_degree))

# В среднем все в этой картине связаны 4.6 личный.
# Мы можем нарисовать такие прямоугольники степеней:
degree_freq = np.array(nx.degree_histogram(G_karate)).astype('float')
plt.figure(figsize=(12, 8))
plt.stem(degree_freq)
plt.ylabel("Frequence")
plt.xlabel("Degree")
plt.show()

3.2 Типы фигур

3.2.1 Модель Эрдоша-Реньи

В модели Эрдоша-Реньи мы строим модель случайного графа с n узлами. Этот граф генерируется путем рисования ребер между парами узлов (i,j) независимо с вероятностью p. Следовательно, у нас есть два параметра: количество узлов n и вероятность p.

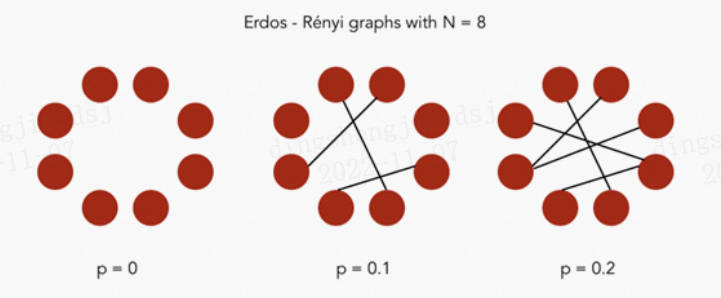
Эрдош-Реньи картина

существовать Python в сетиx Пакеты используются для создания Эрдош-Реньи Встроенные функции для графиков.

3.3 Основные графовые алгоритмы

3.3.1 Алгоритм поиска пути

Пример иллюстрации клуба каратэ

# 1.кратчайший путь
# кратчайший путь вычисляет кратчайший Взвешенный (если в изображении есть Взвешенный) путь между парой узлов.
# Это можно использовать для определения оптимального направления движения или социальной Процесс разделения между двумя людьми степени.
nx.draw(G_karate, cmap = plt.get_cmap('rainbow'), with_labels=True, pos=pos)
# Это возвращает список минимальных путей между каждым узлом в картине:
all_shortest_path = nx.shortest_path(G_karate)
# Здесь напечатан узел0и остальная часть узла, уменьшенная. путь
print(all_shortest_path[0])
# примернравитьсяузел0иузел26изкратчайший путьда[0, 8, 33, 26]

{0: [0], 1: [0, 1], 2: [0, 2], 3: [0, 3], 4: [0, 4], 5: [0, 5], 6: [0, 6], 7: [0, 7], 8: [0, 8], 10: [0, 10], 11: [0, 11], 12: [0, 12], 13: [0, 13], 17: [0, 17], 19: [0, 19], 21: [0, 21], 31: [0, 31], 30: [0, 1, 30], 9: [0, 2, 9], 27: [0, 2, 27], 28: [0, 2, 28], 32: [0, 2, 32], 16: [0, 5, 16], 33: [0, 8, 33], 24: [0, 31, 24], 25: [0, 31, 25], 23: [0, 2, 27, 23], 14: [0, 2, 32, 14], 15: [0, 2, 32, 15], 18: [0, 2, 32, 18], 20: [0, 2, 32, 20], 22: [0, 2, 32, 22], 29: [0, 2, 32, 29], 26: [0, 8, 33, 26]}

3.3.2 Обнаружение сообщества

Обнаружение сообщества делит узлы на несколько групп на основе заданных показателей качества.

Это часто можно использовать для идентификации социальных сообществ, поведения клиентов или тем веб-страниц. Сообщество — это совокупность связанных узлов. Однако в настоящее время не существует общепринятого определения сообщества, за исключением того, что узлы внутри сообщества должны быть тесно связаны.

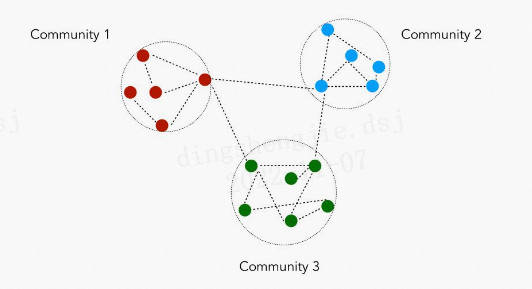
Girvan Newman Алгоритм — широко используемый алгоритм для обнаружения сообществ. Он определяет сообщество, постепенно удаляя стороны внутри сети. Мы называем промежуточное положение «краем». междумежность)». Это пропорционально узлу, проходящему через сторону между парами кратчайшего. Значение количества пути.

Шаги алгоритма следующие:

• Вычислите взаимосвязь всех существующих сторон в сети.
• Удалите самую промежуточную сторону.
• После удаления этой стороны пересчитайте посредничество всех сторон.
• Повторите шаги 2 и 3. Прямое прибытие больше не остается стороной.

from networkx.algorithms import community
import itertools
k = 1
comp = community.girvan_newman(G_karate)
for communities in itertools.islice(comp, k):
    print(tuple(sorted(c) for c in communities))

([0, 1, 3, 4, 5, 6, 7, 10, 11, 12, 13, 16, 17, 19, 21], [2, 8, 9, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33])

import community
partition = community.best_partition(G_karate)
pos = nx.spring_layout(G_karate)
plt.figure(figsize=(8, 8))
plt.axis('off')
nx.draw_networkx_nodes(G_karate, pos, node_size=600, cmap=plt.cm.RdYlBu, node_color=list(partition.values()))
nx.draw_networkx_edges(G_karate, pos, alpha=0.3)
plt.show(G_karate)

3.3.4 Алгоритм центральности

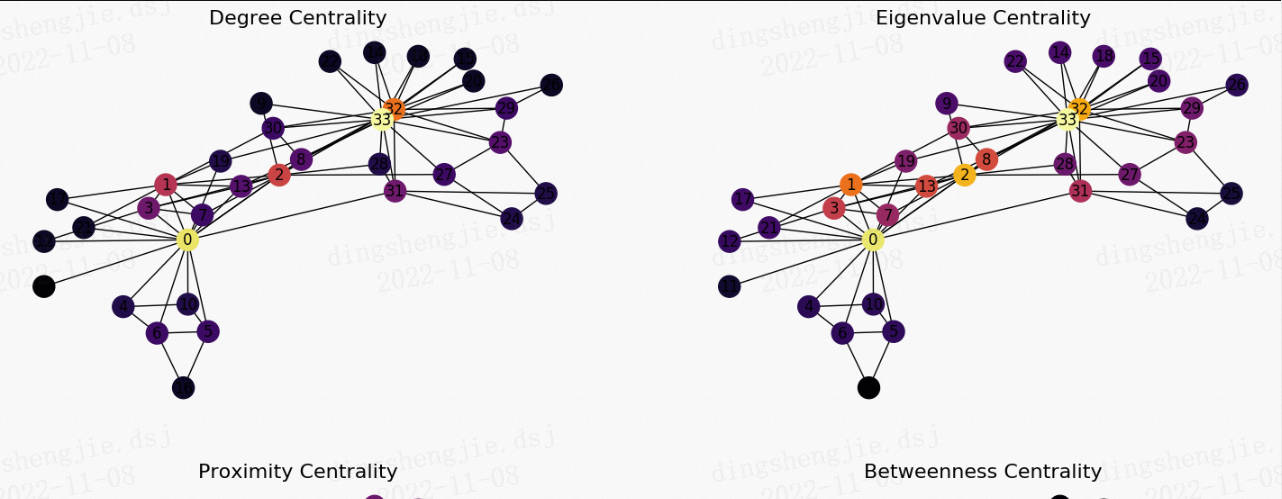
# Plot the centrality of the nodes
plt.figure(figsize=(18, 12))
f, axarr = plt.subplots(2, 2, num=1)
plt.sca(axarr[0,0])
nx.draw(G_karate, cmap = plt.get_cmap('inferno'), node_color = c_degree, node_size=300, pos=pos, with_labels=True)
axarr[0,0].set_title('Degree Centrality', size=16)

plt.sca(axarr[0,1])
nx.draw(G_karate, cmap = plt.get_cmap('inferno'), node_color = c_eigenvector, node_size=300, pos=pos, with_labels=True)
axarr[0,1].set_title('Eigenvalue Centrality', size=16)

plt.sca(axarr[1,0])
nx.draw(G_karate, cmap = plt.get_cmap('inferno'), node_color = c_closeness, node_size=300, pos=pos, with_labels=True)
axarr[1,0].set_title('Proximity Centrality', size=16)

plt.sca(axarr[1,1])
nx.draw(G_karate, cmap = plt.get_cmap('inferno'), node_color = c_betweenness, node_size=300, pos=pos, with_labels=True)
axarr[1,1].set_title('Betweenness Centrality', size=16)

4. Резюме

Из-за нехватки места я поместил в главу 3 только часть программы. Если вам это нужно, вы можете самостоятельно форкнуть исходную ссылку проекта.

добро пожаловатьforkОригинальная ссылка на этот проект：окартинавычислить&картина Обзор основ обучения：Изучение необходимых знаний（Paddle Graph L）https://aistudio.baidu.com/aistudio/projectdetail/4982973?contributionType=1

Потому что раньше я изучал алгоритмы, связанные с извлечением знаний.,Впоследствии, чтобы построить небольшой воротник знаний о домене картина,Может использовать объединение знаний, рассуждение знаний и другие технологии.,Сейчас существование начинает изучать изображение, связанное с вычислительной техникой.

В этом проекте в основном представлены основные типы графов и самые основные атрибуты, используемые для описания графов, а также классические принципы алгоритмов, такие как предварительное обучение (PGL). Наконец, программа демонстрируется, в надежде помочь). всем лучше. Необходимые знания для понимания.

В этом проекте упоминаются: мастер maelfabien, самооценка 3 и г-н Чжэн. ребятасуществоватьблог or Вклады на github

Приветствуем всех на форке, и мы начнем проекты, связанные с графовыми вычислениями, и углубим некоторые технологии извлечения знаний в будущем!