Предисловие

Сигнал линейной частотной модуляции (LFM) имеет большое произведение ширины полосы пропускания и может иметь большую степень сжатия импульса. Это форма сигнала, широко используемая в радиолокационных системах и гидролокаторах. В этой статье в основном проводится теоретическое исследование сигналов линейной частотной модуляции и используется MATLAB для моделирования.

1. Форма сигнала линейной частотной модуляции.

1. Принцип

Сигналы с частотной или фазовой модуляцией используются для получения гораздо более широкой рабочей полосы пропускания. Линейная частотная модуляция (ЛЧМ) является широко используемым методом. В этом случае частота изменяется линейно в пределах ширины импульса либо вверх (повышение частоты), либо вниз (понижение частоты). Полоса пропускания согласованного фильтра пропорциональна полосе развертки и не имеет никакого отношения к ширине импульса. На следующем рисунке показан типичный образец сигнала НЧМ с шириной импульса.

, полоса пропускания

。

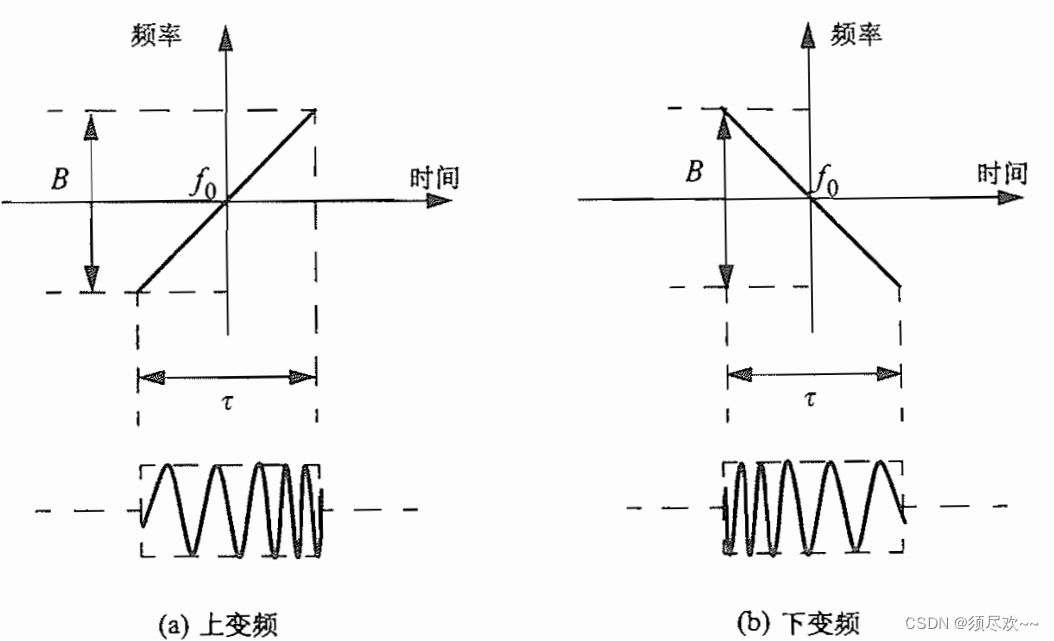
Типичная форма сигнала ЛЧМ

Мгновенную фазу сигнала преобразования с повышением частоты LFM можно выразить как:

в,

- центральная частота радара,

– коэффициент LFM, следовательно, мгновенная частота равна

Таким же образом, мгновенная фаза и частота сигнала понижающего преобразования равны:

2. Выражение во временной области

Типичный чирп-сигнал можно выразить как:

в,

Указывает, что ширина

прямоугольный импульс, то приведенную выше формулу можно записать как:

в:

да

сложный конверт.

3. Выражение в частотной области

Сигнал

Спектр представлен сложной огибающей

Решать,

Комплексный экспоненциальный член представляет собой центральную частоту.

сдвиг частоты. Воля

Выполните преобразование Фурье, чтобы получить

в:

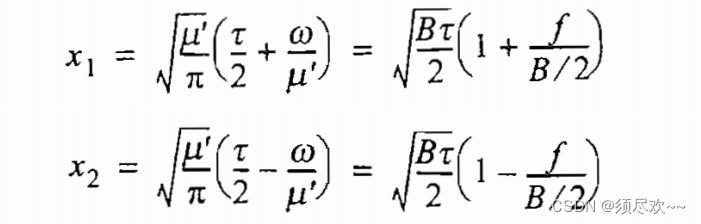
использовать

и

Представляет интеграл Френеля, определяемый следующим образом:

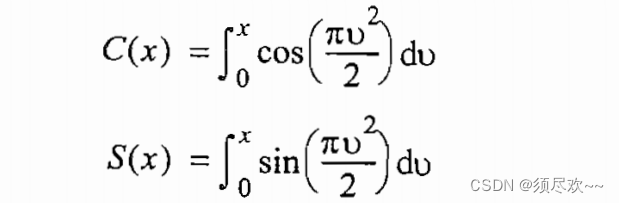
Интеграл Френеля приблизительно равен:

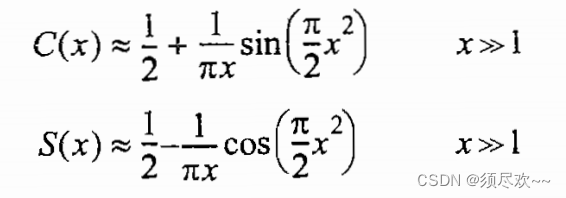
Уведомление:

Подстановка интеграла Френеля в выражение частотной области LFM

,получать:

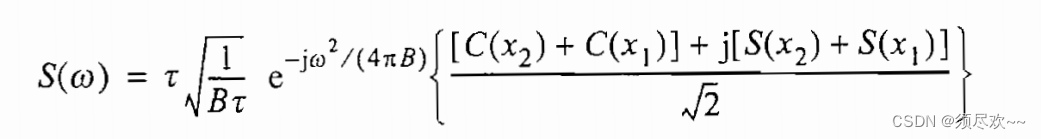
2. Моделирование MATLAB

1. Очки Нефила

①, исходный код MATLAB

clear all
close all
n = 0;
 for x = 0:.05:4
     n = n+1;
     sx(n) = quadl('fresnels',.0,x);
     cx(n) = quadl('fresnelc',.0,x);
 end
plot(cx)
x=0:.05:4; 
plot(x,cx,'k',x,sx,'k--')
grid
xlabel ('x')
ylabel ('Fresnel integrals: C(x); S(x)')
legend('C(x)','S(x)')

② Результаты моделирования.

Изображение ниже

и

существовать

график времени

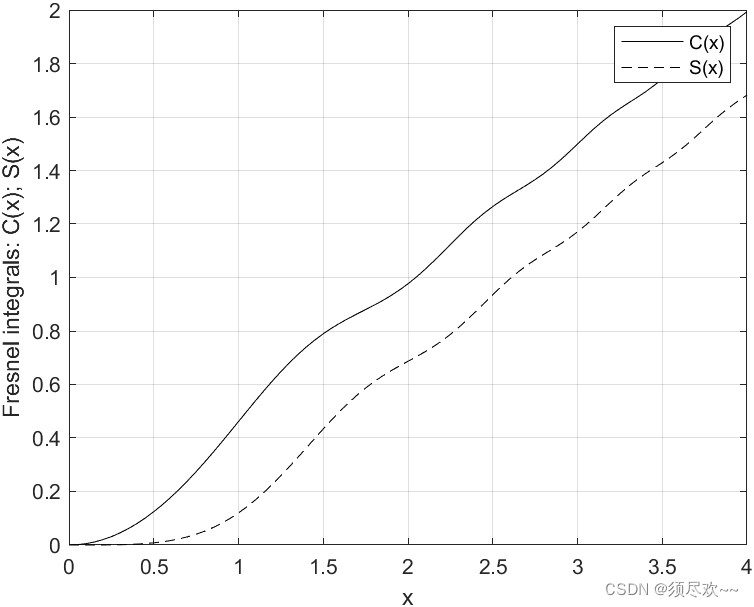
Интеграл Френеля

2、LFM

①, исходный код MATLAB

Ниже приведен типичный график, отображающий действительную часть, мнимую часть и амплитудный спектр сигнала ЛЧМ.

close all
clear all
eps = 0.000001;
%Enter pulse width and bandwidth
B = 200.0e6; %200 MHZ bandwidth
T = 10.e-6; %10 micro second pulse;
% Compute alpha
mu = 2. * pi * B / T;
% Determine sampling times
delt = linspace(-T/2., T/2., 10001); % 1 nano sceond sampling interval
% Compute the complex LFM representation
Ichannal = cos(mu .* delt.^2 / 2.); % Real part
Qchannal = sin(mu .* delt.^2 / 2.); % Imaginary Part
LFM = Ichannal + sqrt(-1) .* Qchannal; % complex signal
%Compute the FFT of the LFM waveform
LFMFFT = fftshift(fft(LFM));
% Plot the real and Immaginary parts and the spectrum
freqlimit = 0.5 / 1.e-9;% the sampling interval 1 nano-second
freq = linspace(-freqlimit/1.e6,freqlimit/1.e6,10001);
figure(1)
plot(delt*1e6,Ichannal,'k');
axis([-1 1 -1 1])
grid
xlabel('Time - microsecs')
ylabel('Real part')
title('T = 10 Microsecond, B = 200 MHz')
figure(2)
plot(delt*1e6,Qchannal,'k');
axis([-1 1 -1 1])
grid
xlabel('Time - microsecs')
ylabel('Imaginary part')
title('T = 10 Microsecond, B = 200 MHz')
figure(3)
plot(freq, abs(LFMFFT),'k');
%axis tight
grid
xlabel('Frequency - MHz')
ylabel('Amplitude spectrum')
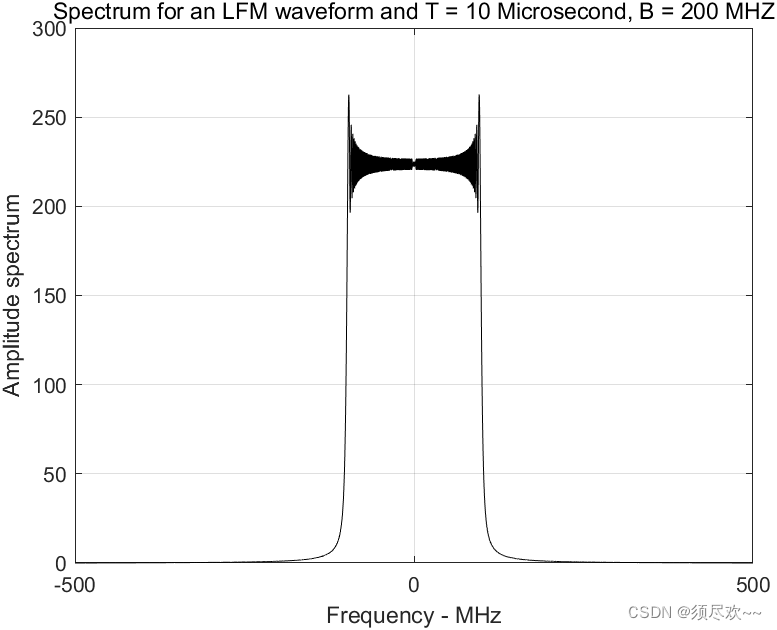
title('Spectrum for an LFM waveform and T = 10 Microsecond, B = 200 MHZ')

Значение B равно 200,0e6, что соответствует полосе пропускания 200 МГц. Значение T равно 10.e-6, что соответствует ширине импульса 10 микросекунд.

② Результаты моделирования.

1) Типичная форма сигнала ЛЧМ, действительная часть

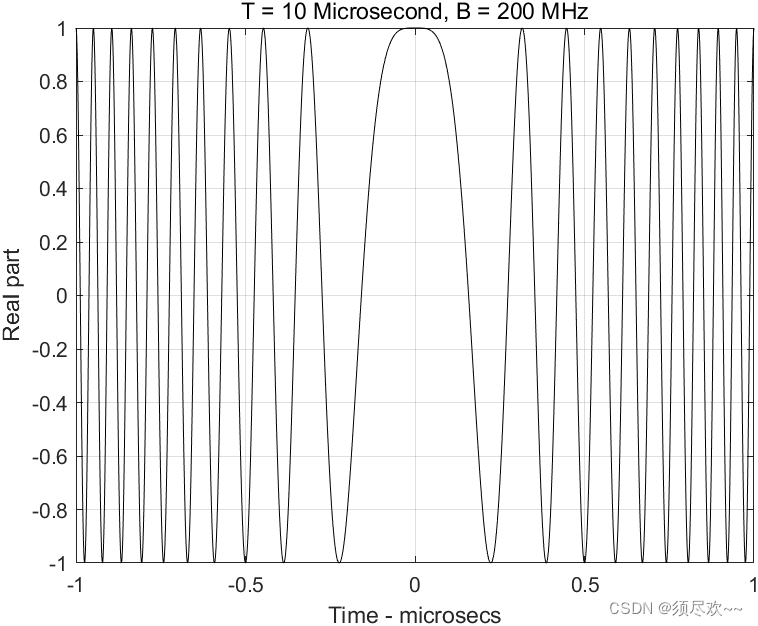
2) Типичная форма сигнала ЛЧМ, мнимая часть

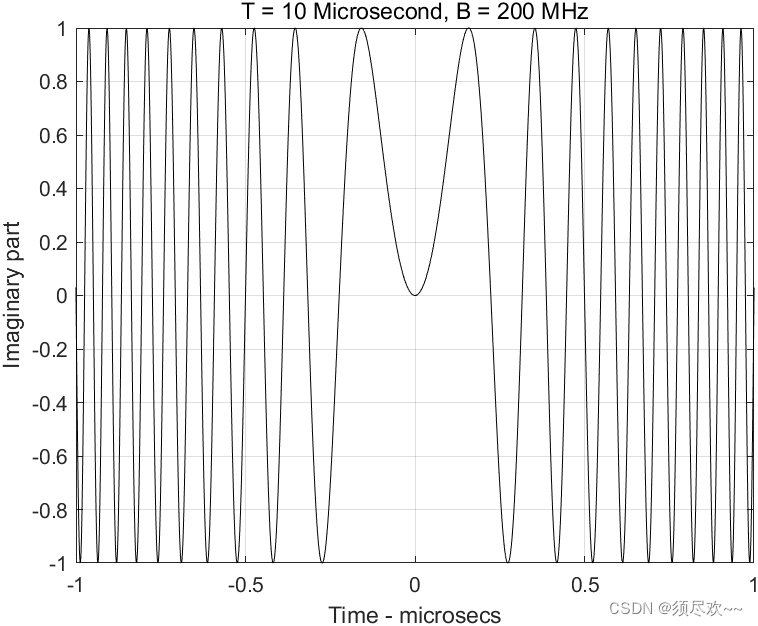
3) Типичный спектр сигнала ЛЧМ

Квадратный спектр на рисунке ниже — это хорошо известный спектр Френеля.