Обучение с подкреплением. Часть 13. Использование глубокого обучения для решения задач в лабиринте, выполнение шагов и код
Обучение с подкреплением было рассмотрено в двенадцатой статье ранее. Проблема лабиринта была решена с помощью Q-обучения. Сегодня используется другой метод: глубокая Q-сеть, или сокращенно сеть DQN.
Что такое ДКН?
Сеть Deep Q (Deep Q-Network, DQN) представляет собой сочетание глубокого обучениеиобучение с Алгоритм поднесений,Предназначен для решения задач принятия решений в многомерных пространствах наблюдения.。оно сделано изDeepMindсуществовать2015предложено в этом году,Успешно используется на нескольких Atari 2600играначальство Обучить агента,Достигнутая производительность, превосходящая производительность игроков-людей.。DQNстал глубинойобучение с Важная веха в области подкреплений – начало использования более глубоких обучение подход к решению сложных задач обучение с Новая эра проблем с поддержанием.
DQNсуществовать许多领域展现了其强大из能力,包括但不限于игра玩法、机器人控制и自动驾驶。DQNи его варианты(нравитьсяDouble DQN、Dueling DQNждать)для последующей глубиныобучение с Исследования и применение подкреплений обеспечивают прочную основу и способствуют быстрому развитию этой области.
Принцип DQN?
DQNОсновная идея заключается в использовании глубокого нейронногосетьприблизитьQ-функция(действиефункция значения),этотQ-функция预测существовать给定состояние Внизвозьми все возможноедействиеожидаемая доходность(накопительное вознаграждение)。традиционныйQАлгоритм обучения основан наТаблица Q来存储и更新每个состояние-действие ДаQценить,但这种方法существовать面对高维состояние空间час变得不切实际。DQNИспользуя глубокие нейронныесеть来克服этот限制,Позволяет обрабатывать сложные, многомерные входные состояния.,Например, изображения.
ключевая инновация
DQN представляет несколько ключевых инноваций, повышающих стабильность и эффективность обучения:
Опыт повтора(Experience Replay):опыт агента(состояние、действие、奖励и Вниз一个состояние)существовать每个час间步被存储существовать一个回放缓冲区中。тренироватьсясетьчас,Из этого буфера случайным образом будет выбрана небольшая партия опыта для обучения.,Это помогает разрушить корреляцию между опытом.,и позволяет повторно использовать каждый опыт несколько раз,Повысьте эффективность данных.Фиксированная цель Q(Fixed Q-targets):为了减少тренироваться过程中из目标Qценить与预测Qценить之间из相关性,DQN использует две сети:один для текущего шагаQценить预测,Другой используется для расчета целевого значения Q. Вес целевой сети получается из прогнозируемой сети копировать периодически (а не на каждом этапе).,Тем самым повышая стабильность обучения.
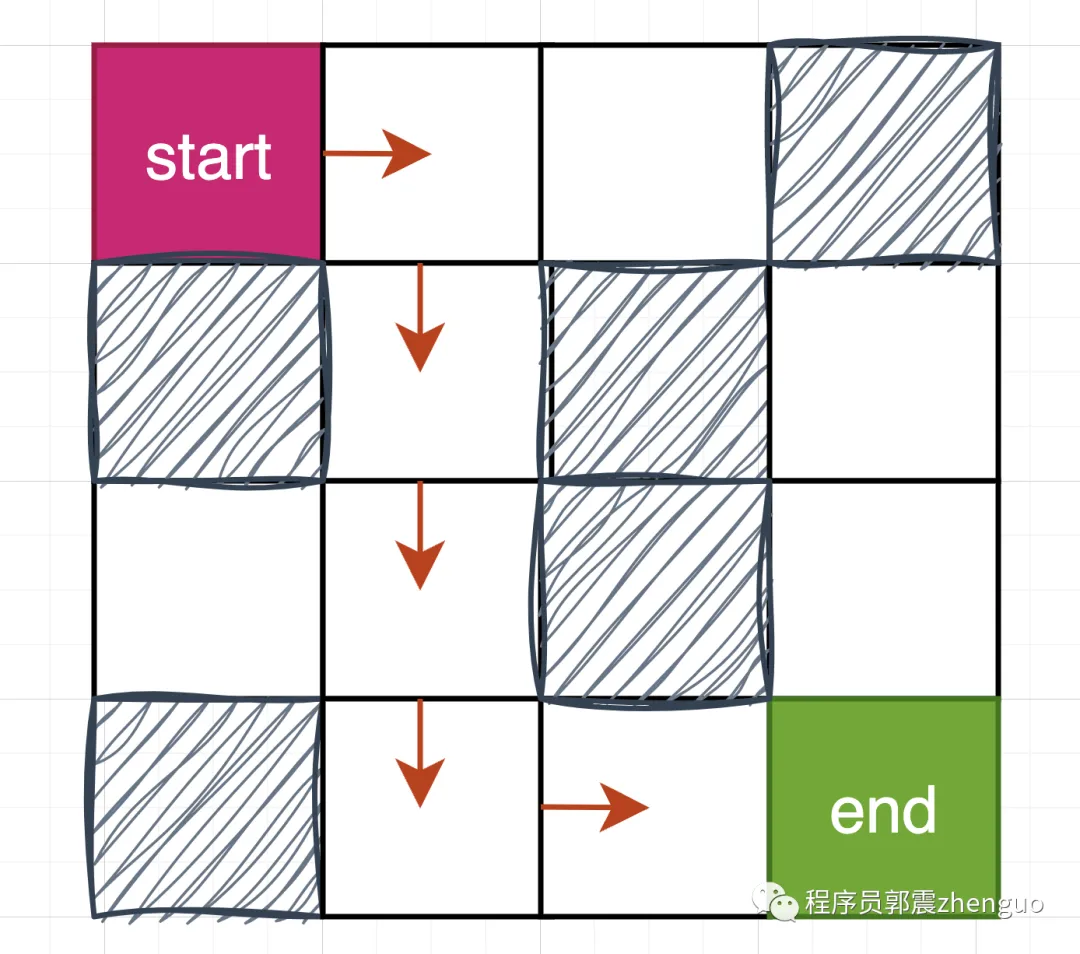
DQN решает проблемы лабиринта
Чтобы использовать Deep Q Network (DQN) для решения проблемы лабиринта, нам сначала нужно создать класс среды, который сможет обрабатывать взаимодействие с агентом: предоставление статуса, принятие действий, возврат нового статуса и вознаграждений и т. д. Далее мы будем использовать DQN, чтобы изучить политику достижения цели в этой среде.
Используйте модули:
import numpy as np
import torch.nn as nn
import torch
from torch.optim import Adam
from collections import deque
import random
import matplotlib.pyplot as plt
Шаг 1. Определите класс среды лабиринта.
class MazeEnv:
def __init__(self):
self.exit_coord = (3, 3)
self.row_n, self.col_n = 4, 4
self.walls = {(0, 3), (1, 0), (1, 2), (2, 2), (3, 0)}
self.state = (0, 0) # исходное состояние
self.actions = [0, 1, 2, 3] # вверх, вниз, влево, вправо
self.reset()
def reset(self):
self.state = (0, 0) # Сбросить положение агента до начальной точки
return self.state
def step(self, action):
row, col = self.state
if action == 0: # начальство
next_state = (max(row - 1, 0), col)
elif action == 1: # Вниз
next_state = (min(row + 1, self.row_n - 1), col)
elif action == 2: # левый
next_state = (row, max(col - 1, 0))
elif action == 3: # верно
next_state = (row, min(col + 1, self.col_n - 1))
else:
raise ValueError("Invalid action")
reward = -1 # Награда по умолчанию
done = False
if next_state in self.walls:
reward = -10
elif next_state == self.exit_coord:
reward = 10
done = True
self.state = next_state if next_state not in self.walls else self.state
return self.state, reward, done
def get_state_size(self):
return self.row_n * self.col_n
def get_action_size(self):
return len(self.actions)
Шаг 2. Определите модель нейронной сети DQN.
# Модель DQN
class DQN(nn.Module):
def __init__(self, input_dim, output_dim):
super(DQN, self).__init__()
self.fc1 = nn.Linear(input_dim, 128)
self.fc2 = nn.Linear(128, 128)
self.fc3 = nn.Linear(128, output_dim)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
output = self.fc3(x)
return output
Шаг третий: Определите восстановление опыта
# Опыт повтора
class ReplayBuffer:
def __init__(self, capacity):
self.buffer = deque(maxlen=capacity)
def push(self, state, action, reward, next_state, done):
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size):
state, action, reward, next_state, done = zip(*random.sample(self.buffer, batch_size))
return np.array(state), action, reward, np.array(next_state), done
def __len__(self):
return len(self.buffer)
Шаг 4. Определите функцию обновления DQN.
def update_model(dqn_model, target_dqn_model, replay_buffer, optimizer, batch_size, gamma):
# от Опыт Случайная выборка серии экспериментов из буфера повтора.
state, action, reward, next_state, done = replay_buffer.sample(batch_size)
# Преобразовать список в тензор
state = torch.FloatTensor(state)
action = torch.LongTensor(action)
reward = torch.FloatTensor(reward)
next_state = torch.FloatTensor(next_state)
done = torch.FloatTensor(done)
# вычислить当前состояние Вниз,принимать практические мерыдействиеизQценить
current_q_values = dqn_model(state).gather(1, action.unsqueeze(1)).squeeze(1)
# Используйте целевую модель DQNвычислить Вниз一состояниеиз最大Qценить
next_q_values = target_dqn_model(next_state).max(1)[0]
# Рассчитать ожидаемое значение Q
expected_q_values = reward + gamma * next_q_values * (1 - done)
# Рассчитать потери
loss = torch.nn.functional.mse_loss(current_q_values, expected_q_values.detach())
# Оптимизатор обнуления градиента
optimizer.zero_grad()
# Обратное распространение ошибки
loss.backward()
# Обновить вес модели
optimizer.step()
Шаг 5: Обучите DQN
# Обучение DQN
def train_dqn(epochs=300):
global epsilon
for epoch in range(epochs):
state = env.reset()
state = np.eye(env.row_n * env.col_n)[state[0] * env.col_n + state[1]]
total_reward = 0
done = False
while not done:
if random.random() < epsilon:
action = random.choice(env.actions)
else:
q_values = dqn_model(torch.FloatTensor(state).unsqueeze(0))
action = torch.argmax(q_values).item()
next_state, reward, done = env.step(action)
next_state = np.eye(env.row_n * env.col_n)[next_state[0] * env.col_n + next_state[1]]
replay_buffer.push(state, action, reward, next_state, done)
state = next_state
total_reward += reward
if len(replay_buffer) > batch_size:
update_model(dqn_model, target_dqn_model, replay_buffer, optimizer, batch_size, gamma)
epsilon = max(epsilon_min, epsilon_decay * epsilon)
print(f'Epoch: {epoch}, Total Reward: {total_reward}')
reward_list.append(total_reward)
if epoch % 10 == 0:
target_dqn_model.load_state_dict(dqn_model.state_dict())
Шаг 6: Анализ результатов
if __name__ == "__main__":
# Инициализировать среду
env = MazeEnv()
# Инициализировать DQN
state_size = env.get_state_size()
action_size = env.get_action_size()
dqn_model = DQN(input_dim=state_size, output_dim=action_size)
target_dqn_model = DQN(input_dim=state_size, output_dim=action_size)
target_dqn_model.load_state_dict(dqn_model.state_dict())
optimizer = Adam(dqn_model.parameters(), lr=1e-4)
replay_buffer = ReplayBuffer(10000)
batch_size = 64
gamma = 0.99
epsilon = 1.0
epsilon_min = 0.01
epsilon_decay = 0.995
reward_list = []
train_dqn()
x = range(len(reward_list))
plt.plot(x, reward_list, label='Line', color='blue')
plt.xlabel("step")
plt.ylabel("reward")
plt.title("DQN to solve the 4*4 maze problem")
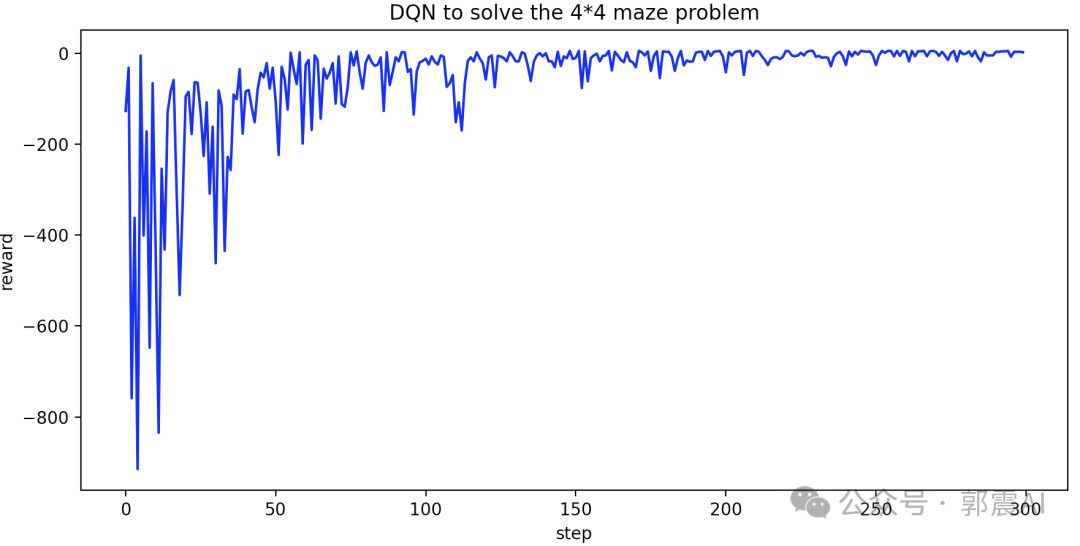
plt.show()Приведенный выше код можно запустить, чтобы нарисовать линейную диаграмму «шаг против вознаграждения». Вы можете видеть, что вознаграждение постепенно увеличивается и, наконец, сходится, примерно за 200 временных шагов.
Используйте полученную модель, чтобы спрогнозировать оптимальный путь ходьбы по лабиринту:
def simulate_optimal_path(model, env):
state = env.reset()
optimal_path = [state] # Запишите статус оптимального пути
done = False
while not done:
state = np.eye(env.row_n * env.col_n)[state[0] * env.col_n + state[1]]
state_tensor = torch.FloatTensor(state).unsqueeze(0)
with torch.no_grad():
action = model(state_tensor).max(1)[1].view(1, 1)
next_state, _, done = env.step(action.item())
optimal_path.append(next_state)
state = next_state
return optimal_path
Вызов:
optimal_path = simulate_optimal_path(dqn_model, env)
print(optimal_path)
Распечатанный оптимальный пешеходный маршрут:
[(0, 0), (0, 1), (1, 1), (2, 1), (3, 1), (3, 2), (3, 3)]
Это пешеходный маршрут на картинке ниже:

кначальство,Используйте ДКН решает проблемы Выполните шаги и код для лабиринта.

Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.

Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).

Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)

Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.

Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
Идеальная интеграция Cursor и DeepSeek API

DeepSeek V3 снижает затраты на обучение больших моделей

Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).

DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».

Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.

Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле

Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.

9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать

Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.

Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)

50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.

Cloud Native|Практика: установка Dashbaord для K8s, графика неплохая

Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности

MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.

Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.

Центр конфигурации————Накос

Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще

[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64

Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике

Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах

Feiniu fnos использует Docker для развертывания личного блокнота Notepad

Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов

[Зона легкого облачного игрового сервера] Управление игровыми архивами


