1. Введение: нейронные сети и уравнения в частных производных.

Уравнения в частных производных можно решать на основе нейронных сетей. Обычно нейронные сети отображают или преобразуют данные из одного конечномерного пространства (например, значения пикселей изображения) в другое конечномерное пространство (например, числа, которые классифицируют изображение, например 1 для кошки и 2). для собаки). Нейронная сеть, которая решает уравнения в частных производных, отображает бесконечное пространство в бесконечное пространство.

Уравнения в частных производных отличаются своей полезностью и сложностью. Например, если кто-то хочет наблюдать поток воздуха возле крыла самолета в двухмерной перспективе, разработчик модели хочет знать, куда течет жидкость в любой точке пространства (также называемой). поле потока) и где Если скорость и давление различны в разное время, необходимо использовать уравнения в частных производных. Этот поток жидкости можно смоделировать с помощью специального уравнения в частных производных, уравнения Навье-Стокса, принимая во внимание законы сохранения энергии, массы и импульса.

В этих случаях разработчики моделей обращаются к численным методам, чтобы преобразовать уравнения в частных производных в набор понятных алгебраических уравнений, предполагая, что эти уравнения могут сохранять небольшие приращения пространства и времени. Численное решение сложных уравнений в частных производных на суперкомпьютере может занять месяцы. Если начальные или граничные условия или геометрия исследуемой системы (например, конструкция крыла) изменяются, решение необходимо перезапустить. Чем меньше используемые приращения (чем тоньше сетка, как говорят исследователи), тем точнее становится модель и тем больше времени требуется для численного решения. Нейронные сети лучше подходят для такой неизвестной функции черного ящика, где входной сигнал является вектором, а выходным сигналом является другой вектор. Если существует функция, которая сопоставляет набор входных векторов с набором выходных векторов, сеть можно обучить этому отображению, и любая функция между двумя конечномерными пространствами может быть аппроксимирована нейронной сетью.

В 2016 году исследователи исследовали, как глубокие нейронные сети, обычно используемые для распознавания изображений, можно использовать для решения уравнений в частных производных. Сначала исследователи сгенерировали данные, используемые для обучения сети: численный решатель рассчитал поле скоростей жидкости, обтекающей простые объекты базовой формы (треугольники, четырехугольники и т. д.) с различными размерами и ориентацией по xy.

2. Как решать уравнения в частных производных на основе нейронной сети

1. Краткий обзор

Основная идея использования нейронных сетей для решения уравнений в частных производных состоит в том, чтобы преобразовать уравнения в частных производных в обучаемую модель, а затем использовать нейронные сети для обучения этой модели.

Вот простой пошаговый обзор:

• 1. Определите задачу. Сначала вам необходимо определить задачу уравнения в частных производных, которую необходимо решить. Это может включать выбор подходящей системы координат, определение граничных и начальных условий и т. д.
• 2. Дискретизация: преобразование непрерывных уравнений в частных производных в дискретные формы. Этого можно добиться, разделив пространственную и временную области на сетки.
• 3. Постройте нейронную сеть. Постройте нейронную сеть для аппроксимации дискретизированного уравнения в частных производных. Входными данными нейронной сети могут быть начальные и граничные условия в точках сетки, а выходными данными может быть решение в этой точке сетки на следующем временном шаге.
• 4. Обучение нейронной сети: используйте данные обучения для обучения нейронной сети. Обучение данных может быть выполнено численными методами Решите уравнения в частных Результаты получены производными методами.
• 5. Прогнозирование: используйте обученную нейронную сеть для прогнозирования решений при новых начальных и граничных условиях.

Следует отметить, что метод нейронных сетей является не точным аналитическим методом, а численным. Поэтому результаты его прогнозирования могут иметь определенные ошибки. Кроме того, обучение нейронных сетей требует большого количества данных и вычислительных ресурсов, поэтому эти факторы необходимо учитывать в практических приложениях.

В целом, использование нейронных сетей для решения уравнений в частных производных является многообещающим подходом, но требует тщательного выбора моделей и обучающих данных для обеспечения точности и надежности результатов прогнозирования.

2. Три основных направления решения уравнений в частных производных на основе нейронных сетей.

2.1 Управление данными

По материалам CNN

1.PDE-Net 2.0 Это метод обнаружения уравнений в частных производных (УЧП), основанный на глубоком обучении. Он обнаруживает (изменяющиеся во времени) УЧП на основе наблюдаемых динамических данных путем комбинирования численных аппроксимаций и символических нейронных сетей. Этот метод обладает высокой гибкостью и выразительностью, а также позволяет изучать дифференциальные операторы и функции нелинейного ответа базовой модели PDE. 2. Метод решения модели трехмерного нестационарного уравнения в частных производных на основе свертки. Метод решения на основе свертки для трехмерных нестационарных моделей уравнений в частных производных был предложен Цзинь Чжэньчжэнем из Школы компьютерных наук и технологий Университета Хуацяо. Этот метод создает формат итерации свертки на основе разностного формата уравнений в частных производных, извлекает ядро ​​свертки и аппроксимирует решение уравнения в частных производных путем сканирования изображения численного решения с помощью ядра свертки. Этот метод непосредственно выполняет итерацию свертки на изображении численного решения, тем самым заменяя процесс решения дискретных линейных уравнений с использованием традиционных численных методов. Численные примеры показывают, что метод итерации свертки GPU Эффективность решения масштабных задач лучше, чем у традиционных ADI Алгоритмы и т. д.

На основе других сетей

1. Нейронная сеть как аппроксиматор функции и ее применение при решении дифференциальных уравнений. Нейронные сети широко используются в качестве аппроксиматоров функций при решении дифференциальных уравнений. Вот некоторые основные концепции и приложения:

• 1. Аппроксимация функций. Нейронная сеть может аппроксимировать любую функцию, регулируя вес сети. Они могут изучить сопоставление между вводом и выводом.,Таким образом, достигается приближение комплексной функции.
• 2. Решение дифференциальных уравнений: для обыкновенных дифференциальных уравнений (ОДУ) или уравнений в частных производных (УЧП),Это можно преобразовать в задачу аппроксимации функции. Аппроксимация решений дифференциальных уравнений с помощью функции нейронной сети,Могут быть достигнуты численные решения дифференциальных уравнений.
• 3. Численное интегрирование: для интегральных задач.,Нейронную сеть можно использовать для аппроксимации функции продукта.,Результат интегрирования затем рассчитывается методом численного интегрирования.
• 4. Краевая задача: Для краевой задачи,Например, решите задачу начального значения ОДУ или задачу граничных условий УЧП.,Решение можно аппроксимировать с помощью нейронной сетевой функции.,И в сочетании с численными методами решения.
• 5. Модель прогнозирования и управления: нейронную сеть можно использовать для построения модели дифференциальных уравнений, позволяющей прогнозировать и контролировать. Изучая взаимосвязь между входом и выходом, можно предсказать будущее состояние системы и обеспечить контроль над ней.

2. Используйте глубокое обучение для решения многомерных уравнений в частных производных. Решение многомерных уравнений в частных производных с использованием глубокого обучения — это активная область исследований, которая сочетает в себе мощные возможности моделирования глубокого обучения с математическим описанием уравнений в частных производных для решения сложных физических задач. Вот некоторые основные концепции и методы:

• 1. Глубокая нейронная сеть: Глубокая нейронная сеть (DNN) — это обычная обучение Модель,Состоит из нескольких слоев нейронов,Можно изучить сложные отношения сопоставления между входными данными и выходными данными.
• 2. Физическая модель: уравнения в частных производных описывают динамическое поведение физических систем.,Например, механика жидкости.、электромагнетизм、Квантовая механика и т. д.
• 3. метод, основанный на данных: глубокое обучение с использованием обширного численного моделирования или экспериментов с данными. обучение Модель, позволяющая изучать поведение и характеристики физических систем.
• 4. Прогноз модели: тренировался глубоко Обучение Модель может использоваться для прогнозирования будущего состояния или реакции физической системы, например, эволюции поля потока, движения объектов и т. д.
• 5. Комбинирование численных методов: глубокое Обучение можно сочетать с традиционными численными методами для повышения точности и эффективности решений.

3. Численные методы решения многомерных параболических уравнений в частных производных и обратных стохастических дифференциальных уравнений на основе глубокого обучения. Численный метод многомерных параболических дифференциальных уравнений в частных производных и обратных стохастических дифференциальных уравнений, основанный на глубоком обучении, представляет собой численный метод, который использует технологию глубокого обучения для решения многомерных параболических дифференциальных уравнений в частных производных и обратных стохастических дифференциальных уравнений. Основная идея этого метода состоит в том, чтобы сопоставить многомерные проблемы с низкомерным пространством, а затем использовать модель глубокого обучения для изучения отношений отображения в низкомерном пространстве. Вот несколько основных шагов:

• 1. Уменьшение пространственной размерности. Сопоставьте многомерные проблемы с низкоразмерным пространством с помощью извлечения признаков или других методов уменьшения размерности.
• 2. глубокое обучение Модель：строитьглубокое обучение Модель,Например, нейронная сеть или сеть кровеносных нервов.,научиться отображать отношения в низкомерном пространстве.
• 3. Численное решение: использование обученного глубокого обучение Модель для приближенного решения многомерных параболических уравнений в частных производных или обратных стохастических дифференциальных уравнений.
• 4. Оценка и оптимизация модели: глубокая оценка путем сравнения с традиционными численными методами или реальными решениями. обучение Модель точности и необходимые оптимизации.

Преимущество этого метода заключается в том, что он может использовать мощные возможности моделирования глубокого обучения для решения многомерных задач и автоматически изучать характеристики и закономерности проблемы. Однако важно отметить, что точность и способность к обобщению моделей глубокого обучения могут зависеть от выбора данных и модели и, следовательно, требуют соответствующей оценки и проверки.

2.2 Физические ограничения

PINN

1. Глубокое обучение, основанное на физике Глубокое обучение на основе физики — это подход, который применяет принципы и концепции физики к глубокому обучению. Целью проекта является использование симметрии, законов сохранения и принципов оптимизации в физике для разработки более мощных и эффективных моделей глубокого обучения. Вот несколько примеров глубокого обучения, основанного на физике:

• 1. Моделирование физических систем. Используйте ньютоновскую механику, термодинамику и другие принципы физики для построения более глубоких систем. обучение Модель, для моделирования поведения и характеристик физических систем.
• 2. Ограничения симметрии: используйте принципы симметрии в физике, такие как вращательная симметрия, трансляционная симметрия и т. д., чтобы ограничить глубокие Структура обучения Модель улучшает способность обобщения и эффективность Модели.
• 3. Закон сохранения: используйте законы сохранения энергии, сохранения импульса и другие законы физики для проектирования глубоких объектов. обучение Модель, чтобы гарантировать, что Модельсуществовать сохраняет сохранение определенных физических величин в процессе обучения.
• 4. Метод оптимизации: изучите методы оптимизации в физике, такие как метод Ньютона, метод градиентного спуска и т. д., для глубокой оптимизации. Параметры обучения Модель.
• 5. Нейронная сеть с информацией о физике: сочетание предшествующих знаний и ограничений в физике.,Проектирование физически значимых структур нейронной сети и функция потерь,Чтобы повысить точность и интерпретируемость Model.

Глубокое обучение, вдохновленное физикой, направлено на объединение принципов и методов физики с глубоким обучением для решения сложных научных и инженерных задач и содействия применению глубокого обучения в области физики.

На основе ПИНН

1. Физическая нейронная сеть с монотонными ограничениями для уравнения Ричардсона-Ричардса. Физическая информационная нейронная сеть (PINN) для уравнения Ричардсона-Ричардса — это метод, основанный на глубоком обучении, для решения уравнения Ричардсона-Ричардса. PINN — это метод, который использует физическую информацию для ограничения нейронных сетей. Он преобразует физические законы в ограничения нейронных сетей, позволяя нейронным сетям лучше моделировать поведение физических систем. Уравнение Ричардсона-Ричардса представляет собой уравнение в частных производных, описывающее процесс вытеснения пласта, и оно широко используется в нефтяной инженерии. Используя PINN для решения уравнения Ричардсона-Ричардса, можно повысить эффективность и точность вычислений, а также лучше управлять сложными моделями резервуаров.

Измеримые данные этикетки

1. Глубокое изучение подземных потоков на основе теоретически управляемых нейронных сетей.

2.3 Физический привод (чисто физические ограничения)

Полносвязная нейронная сеть (FC-NN)

1. Эффективное обучение нейронных сетей физических знаний посредством выборки по важности. Эффективное обучение нейронных сетей физических знаний посредством выборки по важности — это метод обучения, основанный на вероятностных рассуждениях. Выборка по важности — это метод выборки с распределением вероятностей, который позволяет регулировать вероятность выборки в соответствии с важностью выборки, тем самым обеспечивая более эффективное использование ограниченных выборок. При обучении нейронных сетей физических знаний выборка по важности может использоваться для оптимизации процесса обучения и повышения способности к обобщению и точности модели. В частности, эффективное обучение может быть достигнуто за счет следующих шагов:

• 1. Определите целевое распределение вероятностей. В соответствии с характеристиками физической проблемы определите целевое распределение вероятностей, то есть истинное распределение физической величины.
• 2. Разработайте стратегию выборки по важности. Разработайте соответствующую стратегию выборки по важности на основе целевого распределения вероятностей, чтобы получить более целевые репрезентативные выборки.
• 3. Обучение нейронной сети. Используйте выборки, собранные с помощью стратегии выборки по важности, для обучения нейронной сети физических знаний изучению взаимосвязей и законов между физическими величинами.
• 4. Оценка и оптимизация модели: по сравнению с реальными данными или другими эталонными методами.,Оцените производительность обученной нейронной сети, владеющей физическими знаниями.,и провести необходимые оптимизации.

Эффективное обучение нейронных сетей физических знаний посредством выборки по важности может повысить эффективность обучения и способность модели к обобщению, но требует разумного проектирования и корректировки с учетом конкретных проблем.

CNN решает уравнения в частных производных

Физическая информационная геометрия Адаптивная сверточная нейронная сеть для решения параметрических стационарных уравнений в уравнениях в нерегулярных областях Нейронная сеть знаний физики (PINN), основанная на сверточной нейронной сети (CNN), предлагается для эффективного решения параметрических уравнений в частных производных (PDE) в нерегулярных областях без каких-либо помеченных данных. Путем введения эллиптического отображения координат достигается преобразование координат между нерегулярным физическим доменом и регулярным эталонным доменом, тем самым используя мощную классическую магистральную сеть CNN. Численные эксперименты показывают, что этот метод превосходит современный метод PINN, основанный на полностью связанных нейронных сетях, с точки зрения эффективности и точности и может использоваться для решения стационарных уравнений в уравнениях с параметризованными граничными условиями, переменной геометрией, и пространственно изменяющиеся исходные поля.

3. Новые прорывы в решении уравнений в частных производных на основе нейронных сетей.

https://new.qq.com/rain/a/20240229A02ZMH00 В последние годы решатели уравнений в частных производных на основе нейронных сетей получили широкое внимание в различных областях. Среди них квантовый вариационный метод Монте-Карло (NNVMC) внезапно появился в области квантовой химии и продемонстрировал точность, превосходящую традиционные методы, при решении ряда задач. [1, 2, 3, 4]. Пекинский университет и исследовательский отдел Bytedance ByteDance Research совместно разработанная вычислительная среда Forward Laplacian инновационное использование Laplace Расчет оператора прямого распространения: NNVMC Он обеспечивает десятикратное ускорение работы в этой области, тем самым значительно сокращая вычислительные затраты и достигая многих целей в этой области. State of the Искусство также помогает этой области решать больше научных проблем. Эта работа основана на книге «А. computational framework for neural network-based variational Monte Carlo with Forward Лапласа» опубликована в ведущем международном журнале «Nature». Machine Intelligence», соответствующий код имеет открытый исходный код.

• Кодовый адрес:
• https://github.com/bytedance/LapNet
• https://github.com/YWolfeee/lapjax

Эта работа привлекла пристальное внимание соответствующих исследователей, как только она была предложена, вокруг этой работы и структуры программирования было реализовано несколько проектов с открытым исходным кодом. JAX В него также планируется включить эту работу. Эту работу проводили совместно исследовательская группа Ван Ливея в Школе разведки Пекинского университета, исследовательская группа Чэнь Цзи в Школе физики и исследовательский отдел ByteDance. ByteDance Research В состав авторов, разработанных совместно, входят несколько докторантов Пекинского университета. ByteDance Research упражняться. Краткое введение Квантово-вариационный метод Монте-Карло на основе нейронных сетей (NNVMC) стал - Передовая технология в области вычислений ab initio. Он имеет преимущества высокой точности и широкого диапазона применения. Однако его ахиллесовой пятой является высокая вычислительная стоимость, что также ограничивает применение этого метода в практических химических задачах. Автор предлагает новую вычислительную структуру. "Forward Лапласа», используя Laplace Распространение операторов вперед значительно улучшается. NNVMC Вычислительная эффективность метода открывает новые возможности для применения искусственного интеллекта в микроскопических квантовых задачах. Введение метода Forward Laplacian рамка существовать NNVMC В методе целевой функцией нейронной сети является энергия микроскопической системы, включая кинетическую энергию и потенциальную энергию. Термин кинетической энергии предполагает вычисление оператора Лапласа нейронной сети, который также NNVMC Самое продолжительное вычислительное узкое место в процессе. Когда существующая автоматическая дифференциальная рамкасуществовать вычисляет оператор Лапласа, необходимо сначала вычислить матрицу Гессе, а затем получить член Лапласа (т. е. след матрицы Гессе). Расчет предложенной автором рамки "Forward Laplacian" Член Лапласа получается напрямую посредством одного прямого распространения, что позволяет избежать расчета матрицы Гессе, тем самым уменьшая масштаб общего расчета и достигая значительного ускорения.

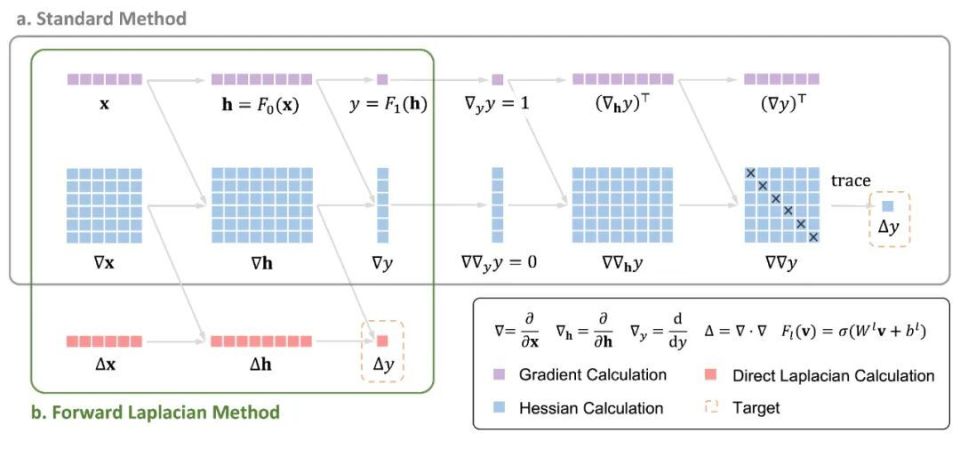
LapNet сеть Помимо эффективного уменьшения размера расчетного графика, Forward Laplacian Еще одна важная особенность кадра заключается в том, что он может эффективно использовать разреженность в вычислениях градиента нейронной сети и предлагать структуру нейронной сети. LapNet。LapNet При увеличении разреженности нейронной сети теряется точность существования, но при этом значительно повышается эффективность сетевых вычислений.

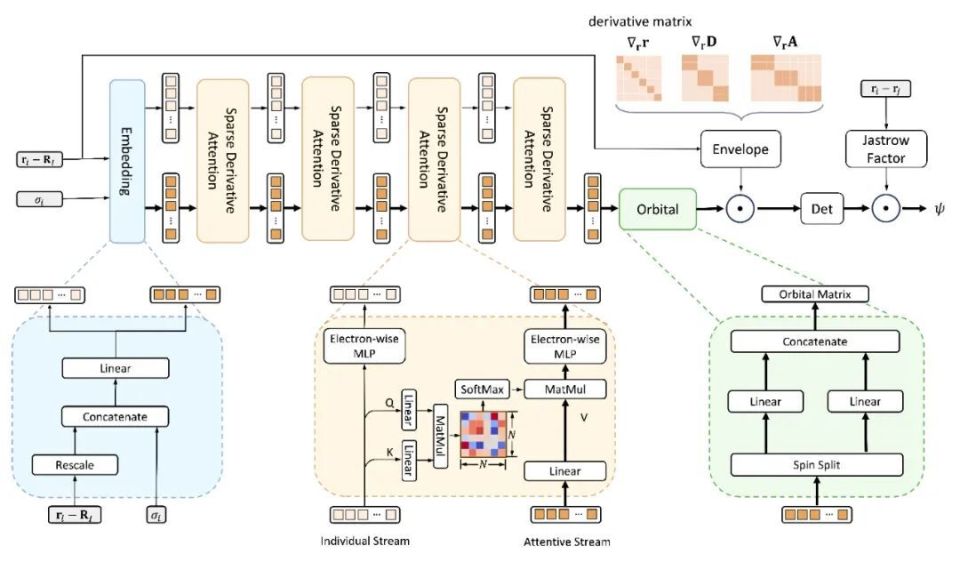
Результат расчета абсолютная энергия Автор впервые сравнивает эффективность и точность метода с современными. NNVMC Сравниваются несколько репрезентативных работ в этой области. Из абсолютной энергияиз Результат В плане расчета автор предложил LapNet существовать Forward Laplacian Эффективность под рамкой в ​​несколько раз выше, чем у эталонной работы, а точность такая же, как у эталонной работы. SOTA Будьте последовательны. Более того, если существуют одни и те же вычислительные ресурсы (т.е. одни и те же GPU час), Лап Нет из Результат расчет может быть существенно лучше предыдущего SOTA。

шкала ускорения С целью более наглядного изучения предложенного автором метода по сравнению с предыдущим SOTA изшкала ускорения, автор существование было протестировано на цепных полиэтиленовых системах разных размеров, и результаты можно ясно увидеть Forward Laplacian принесённый работой O (n) ускориться. здесь n – число электронов в целевой молекуле.

относительная энергия существоватьфизика、Химические исследования,относительная энергияпо сравнению сабсолютная энергия имеет более ясный физический смысл. Автор также провел испытания ряда систем и добился идеальных результатов.