Обзор:

Метрика Маккейба сделал Томас Маккей Предлагается метод измерения сложности, основанный на программном управлении. Также называется цикловой метрикой, цикломатической сложностью (Cyclomatic complexity）, Это программная метрика, также известная как условная сложность или цикломатическая сложность. Он считает, что сложность программы во многом зависит от сложности графа программы. Единая последовательная структура является самой простой. Чем больше циклов и выборок, тем сложнее будет программа.

Метрика Маккейбактеория графовкак инструмент,Сначала нарисуйте изображение программы,Тогда используйте картинкуКоличество петелькакпрограммамера сложности。программа Граф вырожденпрограммаблок-схема。То есть,Выродить каждый символ обработки в блок-схеме программы в узел.,Исходные линии тока соединения с разными символами обработки становятся направленными дугами с разными узлами соединения.,Полученный таким образом ориентированный граф называется программным графом.

в соответствии стеория графов,В сильно связном ориентированном графе G,количество колецV(G)Зависит отк Следующая формула дает：

в,V(G)представляет собой ориентированный графGсерединаКоличество петель,mэто картинкаGсерединаКоличество дуг,nэто картинкаGсерединаКоличество узлов,pэто картинкаGсерединаКоличество сильно связанных компонентов。впрограммасередина,Из точки входа в граф программы вы всегда можете добраться до любого узла графа.,поэтому,программа всегда подключена,Но это не сильно связано. Чтобы сделать граф сильно связным,,Добавьте направленное ребро, представленное пунктирной линией, от точки выхода до точки входа графа.,Сделайте граф сильно связным. Таким образом, сложность цикла можно рассчитать по приведенной выше формуле.

Некоторые из них полезныEпредставлять графикGсерединаКоличество дуг,Прямо сейчас

пример:

Пример 1

использовать Метрика Маккейба вычисляет сложность цикла программы, показанной на рисунке ниже, как ( ）

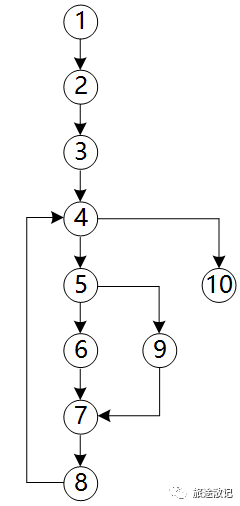
A.1 B.2 C.3 D.4

развязать:

Цикломатическая сложность

, где E — количество ребер в графе потока, а M — количество узлов.

То есть V(G) = 11-10+2 = 3.

Пример 2

Изображение ниже протестировано с использованием метода белого ящика. На рисунке изображены пути ( ). Использование метрики Мак Кейба для расчета сложности цикла графа программы: ( )

Вопрос 1 Варианты A.3 B.4 C.5 D.6

Вариант вопроса 2 А.3 Б.4 В.5 Г.6

развязать:

Пометьте все узлы порядковыми номерами. Согласно схеме можно найти всего 4 различных пути:

1-2-3-11； 1-2-3-4-5-6-10-11； 1-2-3-4-5-7-9-10-11； 1-2-3-4-5-7-8-9-10-11。

Выберите вариант Б в первый раз.

По формуле расчета цикломатической сложности

, выберите вариант B во второй раз.

Пример 3

Определите блок-схему программы, показанную ниже. Тесты покрытия требуют как минимум ( ) тестовые случаи. использовать Метрика Маккейба вычисляет его цикломатическую сложность как ( ）。

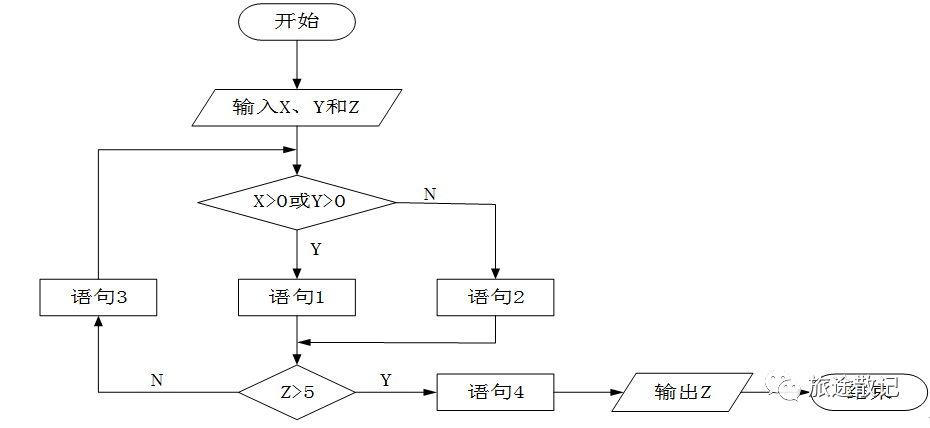
Варианты вопроса 1 A.2 B.3 C.4 D.5

Вариант вопроса 2 А.2 Б.3 В.4 Г.5

развязать:

Покрытие решений заключается в разработке достаточного количества тестовых примеров, чтобы каждое суждение в программе получало «истина» и «ложь» хотя бы один раз, то есть каждая истинная и ложная ветвь в блок-схеме программы выполнялась хотя бы один раз. По смыслу вопроса необходимо всего 2 тестовых примера;

По формуле расчета цикломатической сложности

Охват решений (охват филиалов)

Разница между покрытием решений и условным покрытием

Разница между покрытием условий, покрытием путей, покрытием операторов и покрытием ветвей при тестировании программного обеспечения

Пример 4

Используйте метод тестирования белого ящика для проверки блок-схемы, показанной на рисунке ниже. Если вы хотите обеспечить покрытие путей, вам необходимо как минимум (. ) тестовые случаи. использовать Метрика Маккейба вычисляет сложность цикла этой программы как ( ）

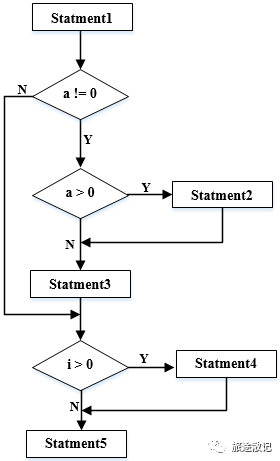
Варианты вопроса 1 A.3 B.4 C.6 D.8

Вариант вопроса 2 А.1 Б.2 В.3 Г.4

развязать:

Вопрос 1 исследует покрытие тестовых путей «белого ящика»: охват всех возможных путей.

в соответствии сблок-схема,Чтобы охватить все возможные пути,Для значения a требуется a=0,a<0,a>0Три варианта использования,И дляiСтоимостьi>0иi<=0Два варианта использования,Перестановка и комбинация,Всего необходимо 6 наборов тестов, чтобы охватить все возможные пути.

Вопрос 2 Для расчета цикломатической сложности по формуле

, где E — количество ребер в графе потока, а N — количество узлов.

。

Пример 5

использовать Метрика Маккейба вычисляет цикломатическую сложность следующего графа программы как ( ）

Вариант вопроса 1

A.2 B.3 C.4 D.5

развязать:

Метрика Маккейба сначала рисует диаграмму программы, а затем использует формулу V(G) = m-n+2 для расчета сложности цикла, где m — количество направленных дуг, а n — количество узлов.


10-8+2=4。

Пример 6

Выполните проверку покрытия путей для следующего псевдокода программы (используйте отступы для обозначения блоков программы), для чего требуется как минимум ( ) тестовые случаи. использовать Метрика Маккейба вычисляет его цикломатическую сложность как ( ）。

Вариант вопроса 1

A.2 B.4 C.6 D.8

Вариант вопроса 2 А.2 Б.3 В.4 Г.5

По этому вопросу,вариант использования(x,y,z) соответственно (1,1,0）（1,-1,0）（-1,0,1）（-1,0,-1）,Эти 4 тестовых варианта использования могут пройти все возможные пути. Потому что в псевдокоде,мы можем видеть,когдаx>0час,Просто нужноYсоответственно взять больше, чем0ине больше, чем0ценить Прямо сейчас да, z не участвует в сравнении, когда x не больше 0, нужно брать только значения z больше 0 и не больше 0 соответственно Прямо сейчас Да, в сравнении не участвует, нужно всего 4 варианта использования Прямо сейчас Может。

Для второго пространства преобразование в граф узлов выглядит следующим образом:

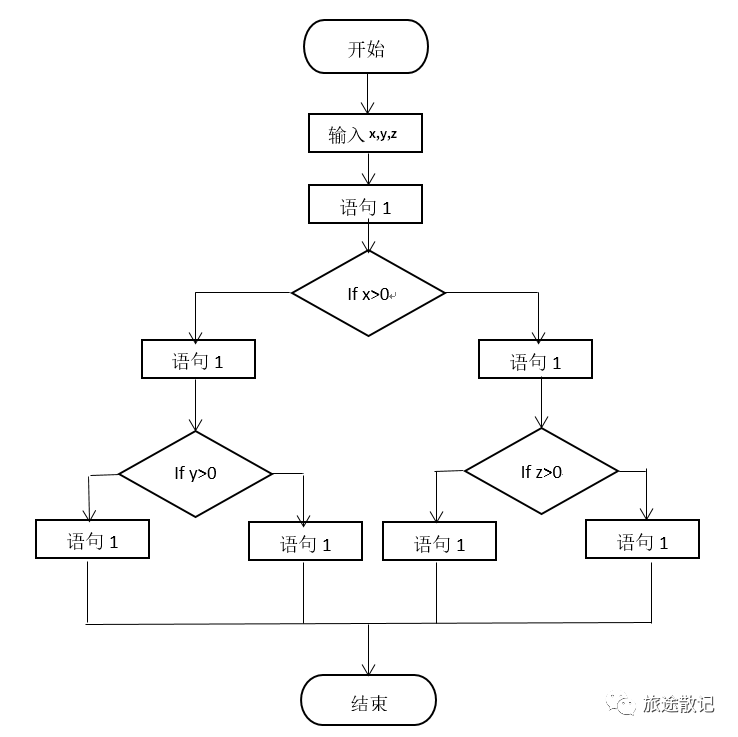
в соответствии с

, где m — дуга ориентированного графа, равная 15, n — количество вершин ориентированного графа, равная 13, 15-13+2=4, то есть комплексный цикл равен 4.

Пример 7

В блок-схеме программы, показанной ниже, есть ( ) разные простые пути. Принять Метрику Маккейба вычисляет сложность цикла графа программы как ( ）

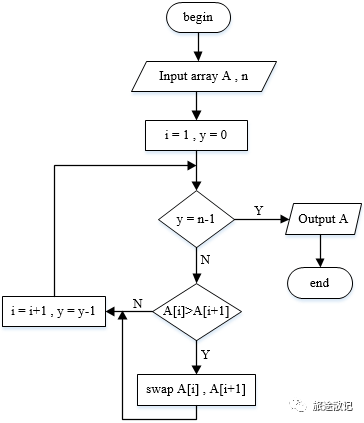
Вариант вопроса 1

A.3 B.4 C.5 D.6

Вопрос 2 варианта

A.3 B.4 C.5 D.6

развязать:

Цикломатическая количественно измеряет логическую сложность программы. После изображения графа потока управления программой, Цикломатическая может быть рассчитана с использованием любого из следующих трех методов. сложность。

(1) Число регионов в потоковом графе равно Цикломатическая сложность。
（2）График потокаGиз Цикломатическая сложностьV(G)=E-N+2, где E — количество ребер в графе потока, а N — количество узлов.
（3）График потокаGиз Цикломатическая сложностьV(G)=P+1, где P — количество узлов принятия решений в потоковом графе.
Идея расчета этого метода измерения контура заключается в следующем: он учитывает сложность управления, Прямой Сейчас Отраслевая сложность условного выбора.
На картинке три простых суждения. Следовательно, 3 простых пути образуют 3 кольцевые области, а сложность области равна 3

Пример 8

Сложность программного обеспечения в основном отражается на сложности программы. ( ) является мерой безопасности обеспечение Основной параметр сложности. Если используете Метрику Маккейба вычисляет сложность цикла, тогда для графа программы, показанного на рисунке ниже, сложность цикла равна ( ）。

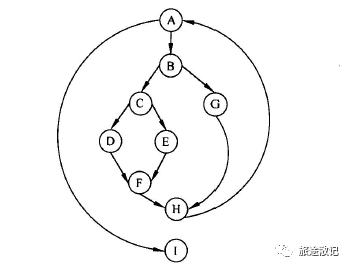
Вариант вопроса 1

A. Количество строк кода B. Количество констант C. Количество переменных D. Количество вызываемых библиотечных функций

Вопрос 2 варианта

A.2 B.3 C.4 D.5

развязать:

Метод измерения количества строк кода использует общее количество строк кода программы как меру сложности программы.

Метрика Маккейба сначала нарисовал диаграмму программы, а затем использовал формулу

Вычислите цикломатическую сложность, где m — количество направленных дуг, а n — количество узлов. В этой задаче количество узлов 9, а дуг 11, поэтому сложность цикла 11-9+2=4.

ссылка:

Мера сложности программы Маккейба

Банк вопросов Сисай