В этой статье подробно рассматривается машинное Концепция матрицы путаницы в обучении, включая ее математические принципы, реализацию Python и ее важность в практическом применении. Мы используем пример диагностики рака легких, чтобы продемонстрировать, как использовать матрицу путаницы для выполнения оценки. модели,И выдвинул ряд уникальных технических идей. Целью статьи является предоставление читателям всестороннего и глубокого понимания,От База до продвинутых приложений.

1. Введение

машинное обучение Часто упускаемая из виду, но важнейшая концепция в науке о данных — это оценка. модели. Возможно, вы создали очень продвинутую Модель, но без надлежащего механизма оценки у вас не будет возможности понять производительность и ограничения Модели. Это матрица путаницы (путаница Матрица) пригодится.

1.1 Что такое матрица путаницы?

Матрица путаницы — это особый макет таблицы, используемый для визуализации производительности алгоритмов обучения с учителем, особенно алгоритмов классификации. В этой матрице каждая строка представляет фактический класс, а каждый столбец — прогнозируемый класс. Каждая ячейка матрицы содержит количество выборок в фактической категории и прогнозируемой категории. С помощью матрицы путаницы мы можем не только рассчитать оценочные показатели, такие как точность, точность и полнота, но также получить более полное представление о производительности модели в различных категориях.

1.2 Зачем нужна матрица путаницы?

1. комплексная оценка：Точность（Accuracy）Обычно люди в первую очередьсосредоточиться показатель, но он может маскировать недостатки Модели в отдельных категориях. Матрица путаницы может предоставить более полную информацию.
2. Экономически эффективный：В некоторых сценариях применения（например, медицинский диагноз、Обнаружение мошенничества и многое другое）,Различные типы ошибок (False Positives и False Негативы) могут иметь различную стоимость или серьезность. Матрица путаницы позволяет нам оценить эти затраты более детально.
3. Оптимизация модели：Матрицы путаницы также можно использовать для оптимизации.Модель,Анализируя, что Модель делает хорошо или плохо,Мы можем внести целевые улучшения.
4. Мост между теорией и практикой：Матрица путаницы помогает не только в теоретическом анализе,Это также облегчает практическое применение. Это дает нам путь от данных к информации.,Затем к мощному инструменту трансформации знаний.

Благодаря этой статье вы получите глубокое понимание всех аспектов матрицы путаницы, включая ее основные концепции, математический анализ и способы реализации практических приложений в средах Python и PyTorch. Независимо от того, являетесь ли вы новичком в машинном обучении или экспертом, желающим глубже понять и применять матрицы путаницы, эта статья предоставит вам ценную информацию.

Далее давайте углубимся в детали матрицы путаницы.

2. Основные понятия

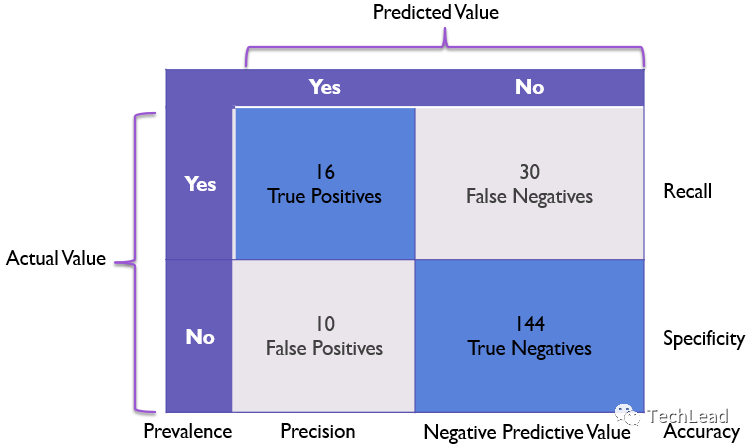
Прежде чем мы углубимся в сложные приложения и математические модели матриц путаницы, мы должны сначала освоить некоторые основные понятия и терминологию. Эти концепции являются основой для понимания и использования матриц неточностей.

Объяснение TP, TN, FP, FN

В задаче двоичной классификации четырьмя основными компонентами матрицы путаницы являются: истинные положительные результаты (TP), истинные отрицательные результаты (TN), ложные положительные результаты (FP) и ложные отрицательные результаты (FN). Мы узнаем о них больше из следующих объяснений и примеров.

True Positive (TP)

Когда модель предсказывает положительный класс и прогноз верен, мы называем его True Positive.

Например, если в системе диагностики рака модель предсказывает, что у пациента рак, а у пациента действительно рак, то это истинный случай.

True Negative (TN)

Когда модель предсказывает отрицательный класс и прогноз верен, мы называем его True Negative.

Например, в описанной выше системе диагностики рака, если модель предсказывает, что у пациента нет рака, а у пациента на самом деле нет рака, то это истинно отрицательный случай.

False Positive (FP)

Когда модель предсказывает положительный класс, но прогноз неверен, мы называем это ложным срабатыванием.

Например, если модель предсказывает, что у пациента рак, но на самом деле у него нет рака, это ложноположительный случай.

False Negative (FN)

Когда модель предсказывает отрицательный класс, но прогноз неверен, мы называем это ложноотрицательным.

Например, если модель предсказывает, что у пациента нет рака, но на самом деле у него рак, это ложноотрицательный случай.

Общие индикаторы оценки

Используя вышеупомянутые четыре основных компонента, мы можем получить различные показатели оценки для более полной оценки эффективности модели.

Поняв эти базовые концепции и показатели оценки, мы можем углубиться в сложные приложения и математические модели матриц путаницы. В следующем разделе мы представим математический анализ матрицы путаницы.

3. Математические принципы

Матрица путаницы — это не только практический инструмент, но и имеющий глубокую математическую основу. Понимание лежащей в ее основе математики может помочь нам более полно оценить и улучшить модель. В этом разделе основное внимание будет уделено этим математическим принципам.

Условная вероятность и теорема Байеса

Матрицы путаницы и множественные показатели оценки связаны с условными вероятностями. В рамках теоремы Байеса мы можем описать эту связь более точно.

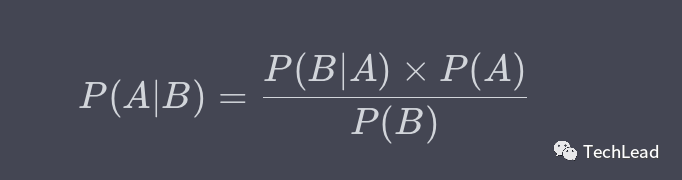
Например, мы можем использовать теорему Байеса для расчета вероятности того, что модель предсказывает положительное наблюдение, при условии, что оно на самом деле положительное.

РПЦ и АУК

Кривая ROC (рабочая характеристика приемника, рабочая характеристика приемника) — это широко используемый инструмент, используемый для отображения истинно положительного уровня (TPR) и ложноположительного уровня (ложно положительного результата, FPR).

AUC (площадь под кривой) — это площадь под кривой ROC, которая используется для количественной оценки общей производительности модели.

Чувствительность и специфичность

Чувствительность (также называемая отзывом) и специфичность обычно используются в таких областях, как медицинская диагностика.

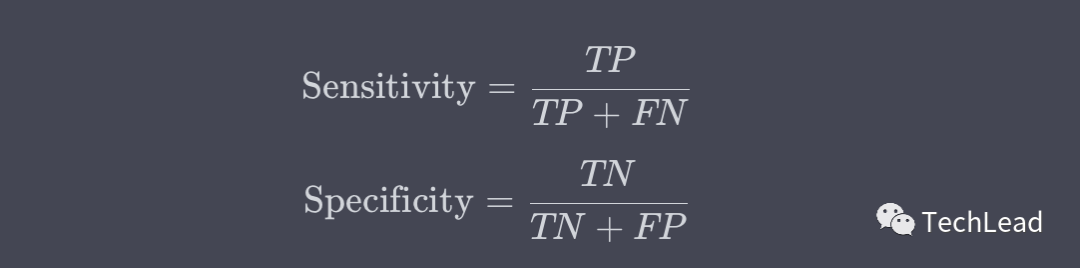
Эти две метрики используются для оценки эффективности модели в положительных и отрицательных классах.

Выбор порога и влияние затрат

В практических приложениях крайне важно выбрать соответствующие пороговые значения, исходя из потребностей бизнеса и затрат. Регулируя порог, мы можем контролировать частоту ложных срабатываний и ложных отрицательных результатов модели для достижения конкретных целей, таких как максимизация точности или полноты.

G-мера и показатель Fβ

Помимо широко используемого показателя F1, существуют и другие показатели, используемые для балансировки точности и полноты, такие как G-мера и показатель Fβ.

Получив более глубокое понимание этих математических принципов,Мы можем не только более точно оценить Модель,Вы также можете внести более подходящие настройки модели для конкретных сценариев применения. следующая часть,Мы перейдем к реальному коду,Показывает, как использовать матрицу путаницы для оценки моделей в среде Python и PyTorch.

4. Реализация Python

Реализация матрицы путаницы не сложна, но реализация ее в коде сделает теоретические знания более конкретными и практичными. В этой части мы будем использовать библиотеки Python и PyTorch для реализации матрицы путаницы и расчета некоторых основных показателей оценки.

Вычисление элементов матрицы путаницы

Сначала давайте воспользуемся кодом Python для расчета элементов матрицы путаницы задачи двоичной классификации: TP, TN, FP, FN.

import numpy as np

# Предположим, y_true — это реальная метка, а y_pred — метка, предсказанная Моделью.
y_true = np.array([1, 0, 1, 1, 0, 1, 0])
y_pred = np.array([1, 0, 1, 0, 0, 1, 1])

# Инициализируйте элементы матрицы путаницы
TP = np.sum((y_true == 1) & (y_pred == 1))
TN = np.sum((y_true == 0) & (y_pred == 0))
FP = np.sum((y_true == 0) & (y_pred == 1))
FN = np.sum((y_true == 1) & (y_pred == 0))

print(f"TP: {TP}, TN: {TN}, FP: {FP}, FN: {FN}")

Выход:

TP: 3, TN: 2, FP: 1, FN: 1

Рассчитать показатели оценки

Используя элементы матрицы путаницы, мы можем затем рассчитать некоторые основные показатели оценки, такие как точность (Accuracy), прецизионность (Precision), скорость отзыва (Recall) и показатель F1 (F1-Score).

# Рассчитать показатели оценки
accuracy = (TP + TN) / (TP + TN + FP + FN)
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1_score = 2 * (precision * recall) / (precision + recall)

print(f"Accuracy: {accuracy:.2f}, Precision: {precision:.2f}, Recall: {recall:.2f}, F1-Score: {f1_score:.2f}")

Выход:

Accuracy: 0.71, Precision: 0.75, Recall: 0.75, F1-Score: 0.75

Реализация PyTorch

Для моделей глубокого обучения с использованием PyTorch нам может быть удобнее использовать встроенные функции для расчета этих показателей.

import torch
import torch.nn.functional as F
from sklearn.metrics import confusion_matrix

# Предположим, что logits — это выходные данные модели, а метки — настоящие метки.
logits = torch.tensor([[0.4, 0.6], [0.7, 0.3], [0.2, 0.8]])
labels = torch.tensor([1, 0, 1])

# Используйте softmax для получения прогнозируемых вероятностей
probs = F.softmax(logits, dim=1)
predictions = torch.argmax(probs, dim=1)

# Используйте sklearn, чтобы получить матрицу путаницы
cm = confusion_matrix(labels.numpy(), predictions.numpy())
print("Confusion Matrix:", cm)

Выход:

Confusion Matrix: [[1, 0],
                   [0, 2]]

Таким образом, мы можем использовать Python и PyTorch для реализации матрицы путаницы и связанных с ней индикаторов оценки. В следующем разделе мы покажем на примерах, как применять эти концепции в реальных проектах.

5. Пример анализа

Теория и код — важные инструменты для понимания матриц путаницы, но их конечная цель — применить их к реальным проблемам. В этом разделе мы будем использовать конкретный пример – диагностику рака легких – чтобы показать, как использовать матрицу путаницы и соответствующие показатели оценки.

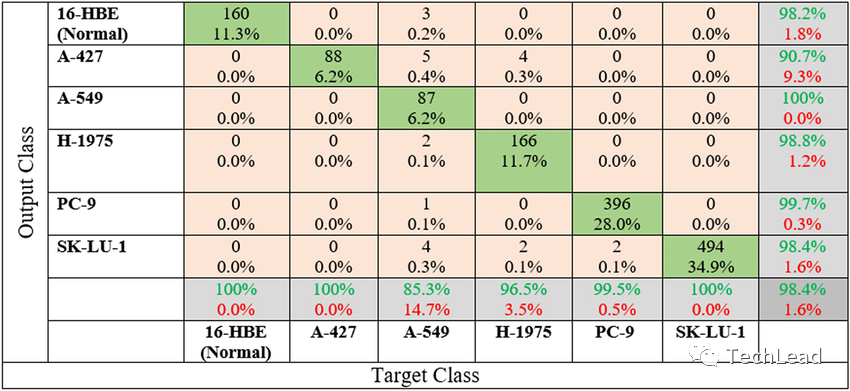
Введение в набор данных

Предположим, у нас есть набор данных о диагностике рака легких, который включает 1000 образцов. Каждый образец имеет набор медицинских изображений и соответствующие метки (1 означает, что у него рак легких, 0 — нет).

Построить модель

В этом примере мы будем использовать PyTorch для построения простой модели нейронной сети. Основная логика кода следующая:

import torch
import torch.nn as nn
import torch.optim as optim

# Модель простой нейронной сети
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(128, 64)
        self.fc2 = nn.Linear(64, 2)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

# Создание модели, оптимизатор и функция потерь
model = SimpleNN()
optimizer = optim.Adam(model.parameters(), lr=0.001)
criterion = nn.CrossEntropyLoss()

Оценка модели

После обучения модели мы будем использовать матрицу путаницы, чтобы оценить ее производительность.

from sklearn.metrics import confusion_matrix

# Предположим, y_test — истинная метка набора тестов, а y_pred — прогнозируемая метка Модели.
y_test = np.array([1, 0, 1, 1, 0, 1, 0])
y_pred = np.array([1, 0, 1, 0, 0, 1, 1])

# Получить матрицу путаницы
cm = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:", cm)

Выход:

Confusion Matrix: [[2, 1],
                   [1, 3]]

Интерпретация индикатора

Из матрицы путаницы мы можем рассчитать такие показатели, как точность, точность, полнота и т. д. Но что еще более важно, поскольку это проблема медицинской диагностики, FN (ложноотрицательный показатель) может означать пропущенный диагноз, что неприемлемо. Следовательно, в этом случае нам, возможно, придется уделять больше внимания запоминаемости или оценке F1, а не просто точности.

в заключение

На этом примере мы видим, что матрица путаницы не только позволяет количественно оценить производительность модели, но также помогает нам настроить модель в соответствии с реальными сценариями применения. Это делает матрицы путаницы незаменимым инструментом в области машинного обучения и науки о данных.

В следующем разделе мы подведем итоги всей статьи и обсудим некоторые сложные темы и перспективы применения матриц путаницы.

6. Резюме

Матрица путаницы — это не только фундаментальная концепция в задачах классификации машинного обучения, но и ключевой инструмент для понимания и оценки эффективности модели. С помощью матрицы мы можем не только количественно оценить качество модели, но и получить глубокое понимание производительности модели в различных аспектах (таких как точность, точность, полнота и т. д.).

1. Важность сценариев применения: Матрица путаницы не является изолированнойинструмент,Его важность заключается в том, как он интерпретируется в зависимости от конкретных сценариев применения (например, медицинский диагноз, финансовое мошенничество и т. д.). в определенных зонах повышенного риска,Некоторые типы ошибок, например ложноотрицательные результаты, могут быть более серьезными, чем другие.
2. Направление оптимизации: Благодаря матрице путаницы мы можем более четко определить направление улучшения Модели. Например, если уровень ложноотрицательных результатов нашей Модели высок, это означает, что необходимо больше внимания. При скорости отзыва может возникнуть необходимость сбалансировать набор данных или скорректировать структуру Модели.
3. Выбор порога: Обычно мы используем 0,5 в качестве порога классификации, но это значение не обязательно является оптимальным. Матрица путаницы может помочь нам оптимизировать Модельпроизводительности путем изменения порога.
4. Проблема мультиклассификации: Хотя в этой статье в основном обсуждается проблема бинарной классификации, матрица путаницы также применима к проблеме. мультиклассификации。существовать Проблема мультиклассификациисередина,Матрица путаницы станет тензором более высокой размерности.,Но основные концепции и методы применения по-прежнему актуальны.
5. Интерпретируемость модели: В реальных приложениях Интерпретируемость Модели часто и Модельпроизводительность одинаково важны. Матрица путаницы дает нам интерпретируемый и интуитивно понятный способ показать преимущества и недостатки Модели.
6. Автоматизация и мониторинг: существовать生产环境середина,Матрицу путаницы можно использовать в качестве инструмента непрерывного мониторинга.,Используется для отслеживания изменений моделипроизводительности.,Это позволяет своевременно обнаруживать корректировки или проблемы в режиме реального времени.

Матрица путаницы — мощный и гибкий инструмент, подходящий не только начинающим пользователям, но и экспертам с глубоким опытом в этой области. Независимо от того, занимаетесь ли вы академическими исследованиями или практикуете, матрицы путаницы должны быть неотъемлемой частью вашего набора инструментов. Надеемся, эта статья поможет вам глубже понять эту тему и максимизировать ее ценность в практических приложениях.