Предисловие

Позвольте мне кратко представиться: блогер, который занимается модельным бизнесом уже пять лет.,Участвовал в десятках проектов по математическому моделированию, больших и малых.,Понимать принципы различных моделей и процесс моделирования каждой модели.и Различные методы анализа вопросов。сейчасПредоставляйте бесплатные идеи и некоторые исходные коды. Пока у меня еще есть время для будущих цифровых и аналоговых соревнований, я обязательно напишу бесплатные идеи с открытым исходным кодом как можно скорее.Блогеры следят за различными конкурсами по математическому моделированию,Блогеры каждого цифрового аналогового конкурса будут совершенно бесплатно писать в этой рубрике новейшие идеи и подробные идеи. Я надеюсь, что нуждающиеся друзья не пропустят статью, тщательно составленную автором.

Основные этапы математического моделирования примерно следующие:

1. определение проблемы：Определите, что вам нужно решитьвопрос。Это включает в себявопрос Исследования на фоне,Поймите, что на самом деле означает вопрос,А также определение граничных условий и допущений для вопроса.
2. Стройте математические модели：будет актуальнымвопроспреобразовать в математикувопрос。Обычно это предполагает Определить переменные、параметр、Ограниченияа такжецелевая Функция (если она оптимизирована, вопрос).
3. Решайте математические модели：Выбирайте правильные математические инструментыиметод Решите модель。这可能包括анализироватьметод、Численные методы、Моделирование и т. д.
4. Проверка и анализ модели：Проверьте эффективность вашей модели, используя реальные данные,Анализ результатов модели,Внесите необходимые корректировки и оптимизации в модель.
5. Написать модельный отчет：Подробные записи процесса построения модели、Этапы решения、Анализ результатов и ограничений модели.

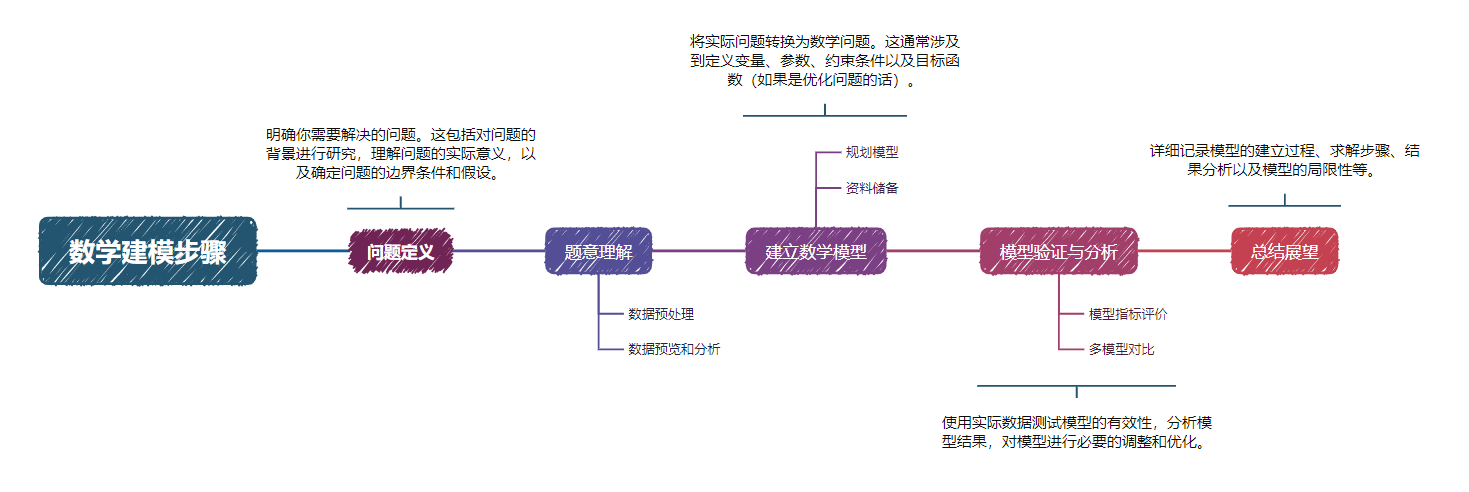
Мы по-прежнему следуем вышеуказанным шагам, чтобы завершить анализ и ответить на вопрос C.

Вопрос C. Предыстория

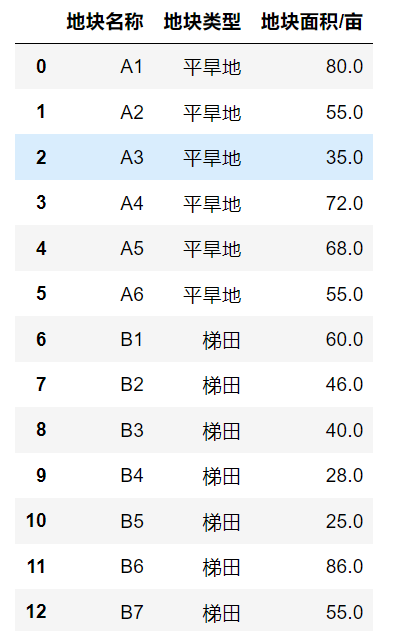
Сельская деревня расположена в горной местности на севере Китая, где температура низкая круглый год. На большей части обрабатываемых земель можно выращивать только один урожай в год. В настоящее время в селе имеется 1201 акр сельскохозяйственных угодий под открытым небом, которые разделены на 34 участка разного размера, в том числе 4 типа: плоская сухая земля, террасные поля, земли на склонах холмов и орошаемые земли. Ровные засушливые земли, террасные поля и земли на склонах холмов подходят для посадки продовольственных культур в течение одного сезона в год; орошаемые земли подходят для посадки одного сезона риса или двух сезонов овощей в год; В поселке 16 обычных теплиц и 4 умных теплицы, каждая с площадью обрабатываемой земли 0,6 соток. Обычные теплицы подходят для посадки одного сезона овощей и одного сезона съедобных грибов каждый год, а умные теплицы подходят для посадки двух сезонов овощей каждый год. На одном и том же участке земли (в том числе в теплицах) каждый сезон можно выращивать разные культуры.

Подробности см. в Приложении 1.

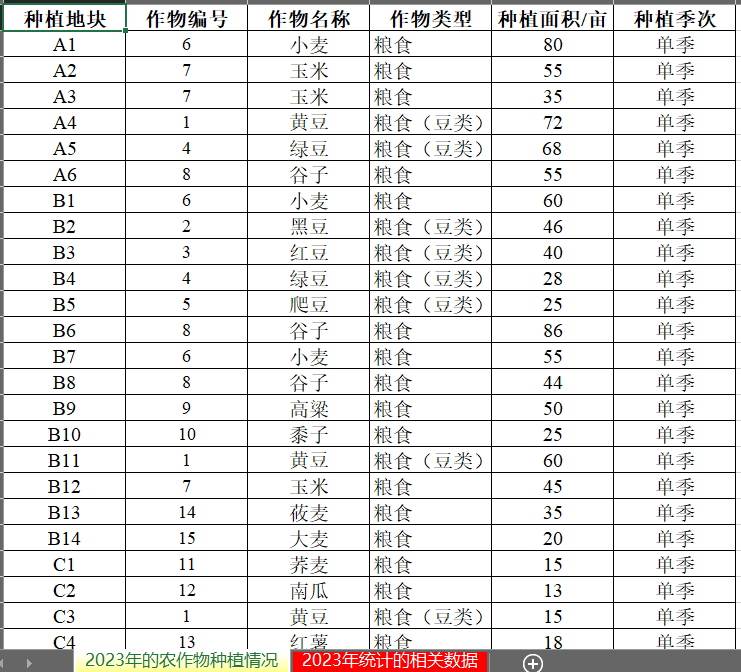
По характеру роста культур нельзя сажать каждую культуру непрерывно на одном участке (в том числе в теплицах), иначе урожайность снизится, поскольку почва, содержащая корневища бобовых культур, благоприятствует росту других культур, каждого участка; будет необходимо выращивать с 2023 года и далее. Все земли (включая теплицы) должны быть засажены бобовыми культурами не реже одного раза в три года. При этом план посадки должен учитывать удобство проведения сельскохозяйственных работ и ведения поля. Например, площади посадки каждой культуры в каждый сезон не должны быть слишком разбросаны, площадь посадки каждой культуры должна быть единой. участок (включая теплицы) не должен быть слишком маленьким и т. д. Посев сельскохозяйственных культур и соответствующие статистические данные в 2023 году представлены в Приложении 2.

Пожалуйста, создайте математическую модель для изучения следующих вопросов:

Вопрос 1

Урожай, выращенный каждый сезон, продается в этом сезоне, при условии, что ожидаемые будущие продажи, затраты на посадку, урожайность с акра и цены реализации различных культур останутся стабильными по сравнению с 2023 годом. Если общий объем производства определенной культуры за сезон превышает соответствующие ожидаемые продажи, избыток не может быть продан нормально. Для следующих двух ситуаций предоставьте оптимальный план посадки сельскохозяйственных культур в деревне на период с 2024 по 2030 год соответственно и заполните результаты в result1_1.xlsx и result1_2.xlsx соответственно (см. приложение 3 для файла шаблона).

(1) Излишки не подлежат продаже, что приводит к растратам;

(2) Излишняя часть будет продана по сниженной цене в размере 50% от цены продажи 2023 года.

Шаг первый: определение проблемы

Этот вопрос посвящен планированию и размещению посевов сельскохозяйственных культур в условиях низких температур в горных районах Северного Китая. В этой области на обычных сельскохозяйственных угодьях под открытым небом можно выращивать продовольственные культуры только один сезон в год, тогда как на орошаемых землях можно выращивать рис или два урожая овощей; в теплицах (обычных и «умных» теплицах) определенные культуры можно выращивать в течение нескольких сезонов. Важным вопросом стало то, как рационально организовать севооборот, смешивание и распределение различных культур на ограниченных сельскохозяйственных угодьях и объектах, чтобы максимизировать экономическую отдачу, удовлетворить требования севооборота и обеспечить плодородие почвы и устойчивое развитие.

Условия расчесывания

Это типичный вопрос сельскохозяйственного экономического математического моделирования.,Включает многоцелевую оптимизацию, планирование и проектирование посадок. первый,Разберем ключевую информацию вопросаи Ограничения:

Ресурсы пахотных земель:

1. Пахотная земля под открытым небом: 1201 акр.,точка34участки
   • Включая плоские засушливые земли, террасные поля, земли на склонах холмов и орошаемые земли.
2. теплица：
   • 16 обычных теплиц (по 0,6 соток каждая)
   • 4 умные теплицы (0,6 соток каждая)

Ограничения посадки:

1. Ограничения севооборота
   • Один и тот же участок земли не может быть засажен постоянно.
   • Каждый участок земли необходимо засаживать бобовыми один раз в три года.
2. Требования к разнообразию посадок
   • Посевные площади каждой культуры в каждый сезон не должны быть слишком разбросаны.
   • Посевная площадь одного участка не должна быть слишком маленькой.

Интерпретация и организация данных

Сбор информации о урожаях

В Приложении 1 перечислены количество, название, тип и подходящий тип обрабатываемой земли, сезонные ограничения и некоторые иллюстративные ограничения. Ключевая информация извлечена ниже:

Классификация культур и ограничения посевного сезона：

• Пищевые культуры (включая фасоль)： Можно использовать на суше.、Террасыи Посадка один раз в год на склоне холма.（весна и летоилиосень,(в зависимости от смысла вопроса),Орошаемые земли (один сезон для риса),Овощи во многие сезоны,Не подходит для многосезонного посева зерновых, кроме фасоли),Теплица (не связанная с выращиванием пищевых продуктов),除бобы蔬菜可能在智慧теплица中种植）。
  • Бобовые продовольственные культуры (соя, черная фасоль, красная фасоль, маш, вьющаяся фасоль) количество: 1-5
  • Прочие продовольственные культуры (пшеница, кукуруза, просо, сорго, просо, гречиха, тыква, батат, овсянка, ячмень) количество: 6-15
  • Рис (№ 16) пригоден только для одного сезона на орошаемых полях.

овощные культуры： Делятся на бобовые овощи (вигна, фасоль, фасоль) и другие овощи (картофель, помидоры, баклажаны, шпинат, зеленый перец, цветная капуста, кочанная капуста, салат, мелкая зелень, огурцы, салат, перец, водяной шпинат, желтая капуста, сельдерей). , пекинская капуста, белая редька, морковь).

• вигна、меч-бобина、фасоль（17-19Число）для овощей（бобы）。
  • Вигна (17): можно сажать в первый сезон на орошаемых землях, в первый сезон в обычных теплицах и в два сезона в умных теплицах.
  • В инструкциях для меч-фасоли (18) и фасоли (19) конкретных сезонных ограничений нет (по умолчанию такое же, как и для обычных овощей. Возможно, это осуществимо в первый сезон орошаемых полей, первый сезон орошаемых полей, первый сезон теплицы и два сезона умных теплиц, но нужно ссылаться на общее правило).
• другие овощи（20-34Число）：
  • На орошаемых землях в первый сезон можно выращивать разнообразные овощи (кроме пекинской капусты, белой редьки и моркови). Во втором сезоне - только одну китайскую капусту (35), белую редьку (36) и морковь (37). ) можно вырастить добрым.
  • В обычных теплицах в первый сезон можно выращивать самые разные овощи (за исключением пекинской капусты, белой редьки и моркови), а во второй сезон — только съедобные грибы.
  • Умные теплицы могут выращивать овощи в оба сезона, но в них также исключены китайская капуста, белая редька и морковь.

культуры съедобных грибов（38-41Число：Юйхуанский гриб、гриб、белый гриб, сморчки): Высаживать его можно только во втором сезоне в обычных теплицах.

Определение посевного сезона (справочные примечания)：

• Орошаемые земли:
  • Сезон 1: примерно с марта по июнь.
  • Второй квартал: примерно с июля по октябрь.
• Обычная теплица:
  • Сезон 1: примерно с мая по сентябрь.
  • Второй сезон: с сентября по апрель следующего года (подходит для съедобных грибов).
• Умная теплица:
  • Сезон 1: примерно с марта по июль.
  • Второй квартал: август ~ примерно февраль следующего года.

специальный запрос：

• Если на одной и той же орошаемой земле посадить две культуры, то в первый сезон можно выращивать разнообразные овощи (за исключением пекинской капусты, белой редьки и моркови), а во втором сезоне среди пекинской капусты можно выращивать только один вид — белокочанную. редис и морковь.
• Китайскую капусту, белую редьку и морковь можно сажать только во второй сезон орошаемых земель и неприменимо к другим типам земель или сезонам.
• В обычных теплицах во второй сезон можно выращивать только съедобные грибы (в первый сезон можно выращивать овощи, но не китайскую капусту, белую редьку и морковь).
• Умные теплицы могут выращивать овощи (за исключением пекинской капусты, белой редьки и моркови) в течение двух сезонов в году.
• Ровные засушливые земли, террасные поля и земли на склонах холмов пригодны только для ежегодного выращивания зерновых (бобовых или небобовых). Рис, орошаемые культуры, специфичные для земель, или овощи не допускаются.
• Рис пригоден для посадки только на орошаемых землях в течение одного сезона (альтернатива посадке овощей) и не пригоден для других типов земель.

Организация информации о земельных участках

(1) Равнина, террасные поля и земли на склонах холмов:

• Ежегодно можно выращивать только один урожай продовольственных культур (включая бобовые, но не рис).

(2) Полив земли:

• Вы можете выращивать только один сезон риса или два урожая овощей в год.
• Если вы выращиваете овощи в два сезона: в первый сезон вы можете выращивать все виды овощей (кроме пекинской капусты, белой редьки и моркови), а во второй — только один вид: пекинскую капусту, белую редьку или морковь. сезон.

(3) Обычная теплица:

• В году два сезона: в первый сезон можно выращивать самые разные овощи (кроме пекинской капусты, белой редьки и моркови), а во второй — только съедобные грибы.

(4) Умная теплица:

• Овощи можно выращивать в оба сезона года (за исключением пекинской капусты, белой редьки и моркови).

(5) Требования к бобовому севообороту (из предыдущего раунда описания, непосредственно в Приложении 1 не повторяются, но известно, что в вопросе упоминается хотя бы одна бобовая культура в течение трех лет)

(6) Требования к непостоянному выращиванию культур (одну и ту же культуру нельзя сажать непрерывно на одном и том же участке)

(7) На одном и том же участке в один и тот же сезон можно сажать разные культуры (комбинированные посадки), но при этом должны соблюдаться минимальные требования к выделению площади (в этом вопросе могут возникнуть последующие ограничения).

Ассоциация участка и культуры

Согласно Приложению 1 и Приложению 2 мы располагаем следующей информацией:

Тип земли и подходящие культуры（См. вложение1анализировать）：

• Ровная сухая земля, террасные поля и склоны холмов: один сезон в году выращиваются только продовольственные культуры (можно считать бобовые и зерновые). Запрещено выращивать рис, овощи и грибы.
• Орошаемая земля: вы можете выбрать один сезон риса или два сезона овощей (первый сезон овощей не включает китайскую капусту (35), белую редьку (36) и морковь (37); второй сезон должен включать китайскую капусту, Выберите один из белой редьки или моркови).
• Обычная теплица: два сезона в году. В первый сезон можно выращивать овощи (исключая номера 35-37), а во второй сезон — только съедобные грибы (38-41).
• Умная теплица: овощи можно выращивать два сезона в году (исключая номера 35-37). Никаких съедобных грибов, выращивания риса или зерна.

выпуск, себестоимость, цена（См. вложение2）：

• В Приложении 2 показаны урожайность на му (цзинь/му), стоимость посадки единицы продукции (юань/му) и диапазон продажной цены (юань/цзинь) каждой культуры на разных типах участков и в разные сезоны посадки.
• Урожайность и стоимость одной и той же культуры могут быть разными на разных типах участков, в разные сезоны и в разных типах теплиц.
• Поскольку в вопросе базовым годом считается 2023 год.,Цены, выпуск и затраты останутся стабильными в будущем.,Доступно во вложении2Возьмите это непосредственно из данных2023годы данных как будущеепараметр：
  • Если цена представляет собой диапазон, в качестве определяемого значения можно использовать среднее значение или эталонную цену диапазона. Например, если цена составляет 2,50–4,00 юаня/цзинь, то за стабильную цену можно принять медианное значение 3,25 юаня/цзинь.
  • В этой модели это записано как:

$$

Y{j,i,s},C{j,i,s},P_{j}

$$

Соответственно представляют урожайность, себестоимость и цену определенной культуры j в зависимости от типа участка и сезонных условий.

В реальной реализации необходимо сначала сопоставить данные в Приложении 2 с соответствующими i и s в зависимости от типа земельного участка и сезона, а затем решить задачу.

Описание математической модели (вопрос 1)

Коллекции и индексы

• Коллекция года: $$ T={2024,2025,…,2030},tεTT = {2024,2025,\dots,2030}, \quad t \in T $$
• Сезонная коллекция (по смыслу вопроса есть в течение года 1 или 2 посевной сезон, то конкретное определение имеет преимущественную силу. Если предположить, что четвертей два, то: $$ S={{1,2}} \quad s \in S $$ Если для некоторых типов земель характерен только один сезон в году, возникнут соответствующие ограничения при принятии соответствующих решений. Второй сезон переменные. решениядля0。
• Сбор участка (включая открытое пространство и теплицу): $$ I={{1,2,…,N}}, \quad i \in I $$ Различные земельные участки имеют разные типы, например, плоские засушливые земли, террасные поля, земли на склонах холмов, орошаемые земли, обычные теплицы и умные теплицы.
• Сбор урожая: $$ J={{1,2,…,M}}, \quad j \in J $$ К сельскохозяйственным культурам относятся зерновые (бобовые и другие зерновые), рис, овощи (бобовые и другие овощи) и съедобные грибы.

параметр

• $A_{i}$: Площадь (акров) участка $i$.
• $Y_{j,i,s}$: В зависимости от типа участка и сезонных условий урожайность с единицы акра (jin/mu) посевной культуры $j$ на участке $i$. Это значение можно определить на основе применимых данных для типа участка и сезона в Приложении 2.
• $ C_{j,i,s}$: стоимость посадки единицы урожая $j$ (юаней/акр) в зависимости от типа участка и сезонных условий.
• $P_j$: Цена продажи ножа $j$ (юань/цзинь). В качестве стабильной цены примите среднее и медианное значение из ценового диапазона.
• $D_{j,s,t}$: Нет. $t$ год ss ожидаемый лимит продаж сезонных культур jj (кошки). При превышении этой суммы,В сценарии (1) дохода нет.,Продается за полцены в сценарии (2).

переменные решения

• $x_{i,j,s,t}≥0$: в $t$ год $s$ сюжет Джию $i$ выращивание сельскохозяйственных культур на $j$ площадь (акров).
• Вспомогательные переменные (используются для обработки превышения и снижения ожидаемого объема продаж):

$Uj, s, t ≥ 0$: объем продукции культуры j в этом сезоне и году, превышающий ожидаемый объем продаж (jin) $U{j,s,t} \geq 0$: $\text{Урожай этого сезона и года } j \text{ Объем производства, превышающий ожидаемый объем продаж (цзинь)}$

$Wj,s,t≥0$: урожайность культуры j в этом сезоне и году ниже ожидаемого объема продаж (jin) $W{j,s,t} \geq 0$: $\text{Урожай этого сезона и года } j \text{ Часть выпуска, которая ниже ожидаемого объема продаж (jin)}$

в оптимальном решении,$U{j,s,t} $ и $W{j,s,t} $ не может быть одновременно положительным.

Ограничения

1. ограничения землепользования： Общая площадь посадок каждого участка в каждый сезон не должна превышать площадь участка: $$ \sum{j} x{i,j,s,t} \leq A_i, \quad \forall i,s,t $$ .
2. Пригодность и сезонные ограничения： Ограничения накладываются на допустимые комбинации типа участка-сезона в зависимости от типа участка и требований сезона сбора урожая (описанных в Приложении 1):

$xi,j,s,t=0$ Если комбинация $ (i,j,s)$ невозможна $x_{i,j,s,t} = 0$ $\quad \text{Если комбинация} (i, j,s)\text{ Невозможно}$

Например: только один сезон продовольственных культур можно сажать на равнинных засушливых землях, террасных полях и склонах холмов; при посадке двух культур овощей на орошаемых землях в первый сезон посевы № 35-37 не высаживаются; а в обычных теплицах можно сажать только одну культуру №35-37, в умных теплицах можно выращивать только съедобные грибы (кроме №35-37); в оба сезона.

1. ограничение прерывистой обрезки： Одну и ту же культуру нельзя сажать на одном и том же участке земли в последовательные сезоны (в том числе в разные годы): $$ y{i,j,s,t} + y{i,j,s',t'} \leq 1 $$ в $(s',t')$ — предыдущий квартал $(s,t)$. Используйте двоичные переменные $y{i,j,s,t} $ указывает, будет ли участок засажен сельскохозяйственными культурами в этом сезоне. $j$, и через логические соотношения $(x{i,j,s,t}>0⇒y{i,j,s,t}=1)(x{i,j,s,t}>0 )$ выполнить.
2. Ограничения трехлетнего севооборота бобовых： Каждый участок должен быть засажен бобовыми не менее одного сезона в течение любых трех последовательных лет:

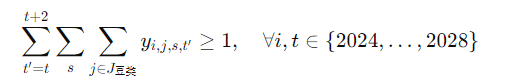
Определение производства и перепроизводство/недопроизводство：

Общий выпуск:

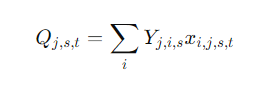
Превзошли ожидания:

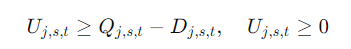
Меньше, чем ожидалось:

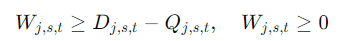
1. Благодаря этим двум ограничениям его можно линейно охарактеризовать $min⁡(Q{j,s,t},D{j,s,t})=D{j,s,t}−U_j$ и $max⁡(Q{j,s,t}−D{j,s,t},0)=U{j,s,t}$。

целевая функция

Вопрос 1 требует решения оптимального плана посадки по двум сценариям.

помнить:

Сценарий (1)：超过部точка滞销无доход

доход = Распродажа по обычной цене $\min(Q{j,s,t},D{j,s,t})$ Сумма вывода превышает лимит.

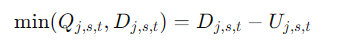
поэтому,

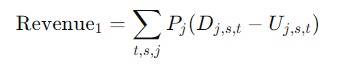
целевая функция：

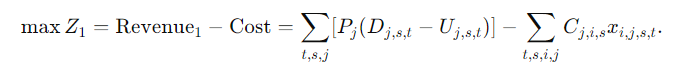
Сценарий (2)：Нажмите на лишняя распродажа за полцены

Если излишки производства составляют $U_{j,s,t}$, то эта часть продается по $0,5P_j$.

В то же время, когда $Q{j,s,t}<D{j,s,t}$ Когда есть недостатки $W{j,s,t}$,Распродажа по обычной Количество цены $D{j,s,t}-W_{j,s,t}$。

Комплексное доступное:

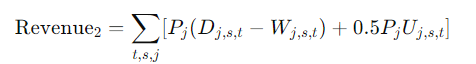
целевая функция：

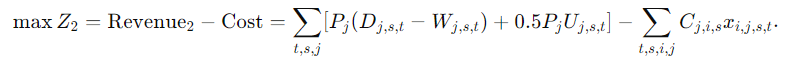
Моделирование на Python

Здесь будут даны основная структура и идеи моделирования. Впоследствии соответствующий словарь параметров и таблица данных могут быть отсортированы на основе прикрепленных данных, а затем считаны в модель.

# Чтобы установить межсезонные ограничения, необходимо знать соответствующую взаимосвязь предыдущего сезона. Например, если в году два сезона, предыдущим сезоном может быть (s-1,t) или Новый год.
# Для связи сезонов предполагается, что S=[1,2], Тогда (s=1,t=2025) прошлый сезон был (s=2,t=2024) и т.д.
def prev_season(s, t):
    # Возвращает данные предыдущего сезона (s', t')
    if s == 1:
        return (2, t-1)
    else:
        return (1, t)
# -----------------------------------------
# Построить модель
model = pyo.ConcreteModel("Farming_Optimization")

# Определить переменные
model.x = pyo.Var(I, J, S, T, domain=pyo.NonNegativeReals) # x_{i,j,s,t}
model.U = pyo.Var(J, S, T, domain=pyo.NonNegativeReals)    # U_{j,s,t}
model.W = pyo.Var(J, S, T, domain=pyo.NonNegativeReals)    # W_{j,s,t}

# двоичная переменная y_{i,j,s,t} Используется для указания, сажать или нет, с использованием метода большой М и логических ограничений.
# для简化,Прямо определено здесьyдлядвоичная переменная
model.y = pyo.Var(I, J, S, T, domain=pyo.Binary)

# -----------------------------------------
# Ограничения

# 1. ограничения землепользования
def land_use_rule(model, i, s, t):
    return sum(model.x[i,j,s,t] for j in J) <= A[i]
model.LandUse = pyo.Constraint(I, S, T, rule=land_use_rule)

# 2. Пригодность и сезонные ограничения
def feasibility_rule(model, i, j, s, t):
    if no_plant[(i,j,s)]:
        return model.x[i,j,s,t] == 0
    return pyo.Constraint.Skip
model.Feasibility = pyo.Constraint(I, J, S, T, rule=feasibility_rule)

# 3. ограничение прерывистой обрезки
# Необходимо следить за тем, чтобы, если в прошлом сезоне на том же участке была посажена та же культура, в этом сезоне эта же культура не будет посажена.
def no_repeated_rule(model, i, j, s, t):
    s_prev, t_prev = prev_season(s, t)
    if t_prev < min(T):
        return pyo.Constraint.Skip
    return model.y[i,j,s,t] + model.y[i,j,s_prev,t_prev] <= 1
model.NoRepeated = pyo.Constraint(I, J, S, T, rule=no_repeated_rule)

# xиyассоциация：когдаx>0时 y=1, иначе y=0
# Вы можете использовать следующие методы: x[i,j,s,t] <= A[i]*y[i,j,s,t]
def x_y_link_rule(model, i, j, s, t):
    return model.x[i,j,s,t] <= A[i]*model.y[i,j,s,t]
model.XYLink = pyo.Constraint(I, J, S, T, rule=x_y_link_rule)

# 4. Ограничения трехлетнего севооборота бобовых
# любому i,t, фасоль выращивают не реже одного раза в три года подряд
# Взяв 3 года как окно t, t+1, t+2
def bean_rotation_rule(model, i, start_t):
    # start_t с 2024 по 2028 год
    # трехлетнее окно = start_t, start_t+1, start_t+2
    # Посевы фасоли удовлетворяют требованию, чтобы y=1 в определенный сезон.
    years = [start_t, start_t+1, start_t+2]
    return sum(model.y[i,j,s,t_] for t_ in years for s in S for j in bean_crops) >= 1
model.BeanRotation = pyo.Constraint(I, [t for t in T if t <= 2028], rule=bean_rotation_rule)

# 5. Определения доходности и превышения/недостатка
# Q_{j,s,t} = sum_i Y_{j,i,s} x_{i,j,s,t}
def Q_expr(model, j, s, t):
    return sum(Y[(j,i,s)]*model.x[i,j,s,t] for i in I)
model.Q = pyo.Expression(J, S, T, rule=Q_expr)

# Избыток: U_{j,s,t} >= Q_{j,s,t}-D_{j,s,t}
def U_rule(model, j, s, t):
    return model.U[j,s,t] >= model.Q[j,s,t] - D[(j,s,t)]
model.UConstraint = pyo.Constraint(J, S, T, rule=U_rule)

# Недостатки: W_{j,s,t} >= D_{j,s,t}-Q_{j,s,t}
def W_rule(model, j, s, t):
    return model.W[j,s,t] >= D[(j,s,t)] - model.Q[j,s,t]
model.WConstraint = pyo.Constraint(J, S, T, rule=W_rule)


# -----------------------------------------
# целевая функция
# Для вопроса 1 у нас есть два сценария:
# Сценарий (1): Никаких лишних деталей
#   Revenue = sum_{t,s,j} P_j*(D_{j,s,t}-U_{j,s,t})
# Сценарий (2): Излишки продаются за полцены.
#   Revenue = sum_{t,s,j} [P_j(D_{j,s,t}-W_{j,s,t}) + 0.5P_j U_{j,s,t}]

# Сначала мы можем определить параметр scenario Указывает выбранную сцену
scenario = 1  # Измените его на 2, чтобы переключить Сценарий. (2)

def obj_rule(model):
    if scenario == 1:
        # Сценарий (1)
        revenue = sum(P[j]*(D[(j,s,t)] - model.U[j,s,t]) for j in J for s in S for t in T)
    else:
        # Сценарий (2)
        revenue = sum(P[j]*(D[(j,s,t)] - model.W[j,s,t]) + 0.5*P[j]*model.U[j,s,t] for j in J for s in S for t in T)
    cost = sum(C[(j,i,s)]*model.x[i,j,s,t] for i in I for j in J for s in S for t in T)
    return revenue - cost

model.OBJ = pyo.Objective(rule=obj_rule, sense=pyo.maximize)

# -----------------------------------------
# Решите модель
solver = pyo.SolverFactory('gurobi')  # или cplex/glpk
results = solver.solve(model, tee=True)

# Вывод результатов в файл
# Предположим, что вам нужно x_{i,j,s,t} Результаты выводятся в result1_1.xlsx или result1_2.xlsx
# Использование pandas для записи в Excel — распространенный метод, здесь мы только проиллюстрируем:
import pandas as pd

solution_x = []
for i in I:
    for j in J:
        for s in S:
            for t in T:
                val = pyo.value(model.x[i,j,s,t])
                if val > 1e-6: # Если есть положительная посадочная площадка
                    solution_x.append([i,j,s,t,val])

Этот вопрос на данный момент здесь, и мы добавим ответы на другие вопросы позже. Содержание слишком обширное и требует глубокого понимания.