KAN: Полный перевод статьи Колмогорова – Арнольда Сетей
KAN: Kolmogorov–Arnold Networks https://arxiv.org/pdf/2404.19756
6 Обсуждение
Application aspects: We have presented some preliminary evidences that KANs are more effective than MLPs in science-related tasks, e.g., fitting physical equations and PDE solving.
We expect that KANs may also be promising for solving Navier-Stokes equations, density functional theory, or any other tasks that can be formulated as regression or PDE solving.
We would also like to apply KANs to machine-learning-related tasks, which would require integrating KANs into current architectures, e.g., transformers – one may propose “kansformers” which replace MLPs by KANs in transformers.
KAN as a “language model” for AI + Science
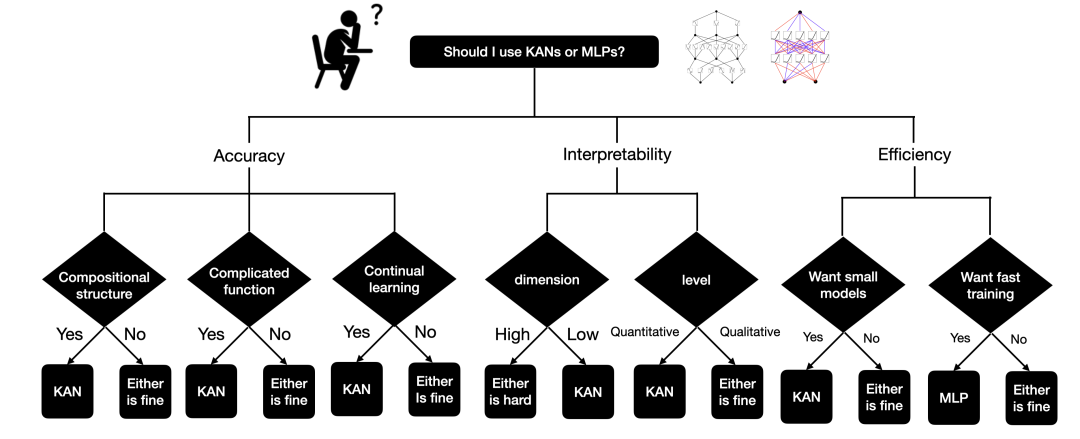
В настоящее время КАН Самым большим узким местом является низкая скорость обучения. При таком же количестве параметров КАНы обычно чем MLPs медленный 10 раз. если быть честным,авторНикаких усилий по оптимизации не предпринималось. KANs эффективность, думаю KANs Скорость обучения


Резюме (переведено для быстрого ознакомления)
Вдохновленные теоремой о представлении Колмогорова-Арнольда, мы предлагаем сети Колмогорова-Арнольда (KAN) в качестве многообещающей альтернативы многослойным персептронам (MLP). В то время как MLP имеют фиксированные функции активации на узлах («нейроны»), KAN имеют обучаемые функции активации на ребрах («веса»). KAN не имеют линейных весов — каждый весовой параметр заменяется одномерной функцией, параметризованной в виде сплайна. Мы показываем, что это, казалось бы, простое изменение позволяет KAN превзойти MLP с точки зрения точности и интерпретируемости. С точки зрения точности, меньшие KAN могут достичь сопоставимой или большей точности, чем более крупные MLP, с точки зрения подбора данных и решения PDE. И теоретически, и эмпирически KAN обладают более быстрыми законами нейронного расширения, чем MLP. С точки зрения интерпретируемости, KAN можно визуализировать интуитивно и легко взаимодействовать с пользователями. Имея два примера из математики и физики, KAN оказались полезными «соавторами», помогающими учёным (заново) открыть законы математики и физики. Подводя итог, можно сказать, что KAN являются многообещающей альтернативой MLP, открывающей возможности для дальнейшего совершенствования современных моделей глубокого обучения, основанных на MLP.
1 Введение
Многослойные перцептроны (MLP) [1, 2, 3], также известные как полносвязные нейронные сети прямого распространения, являются фундаментальными строительными блоками современных моделей глубокого обучения. Важность MLP очевидна, поскольку они являются моделью по умолчанию, используемой для аппроксимации нелинейных функций в машинном обучении, а их выразительные возможности гарантируются универсальной теоремой аппроксимации [3]. Однако являются ли MLP лучшими нелинейными регрессорами, которые мы можем создать? Несмотря на широкое распространение, MLP имеют существенные недостатки. Например, в Трансформерах [4] MLP потребляют почти все невстроенные параметры и, как правило, менее интерпретируемы (по сравнению со слоями внимания) без последующих инструментов анализа [5].
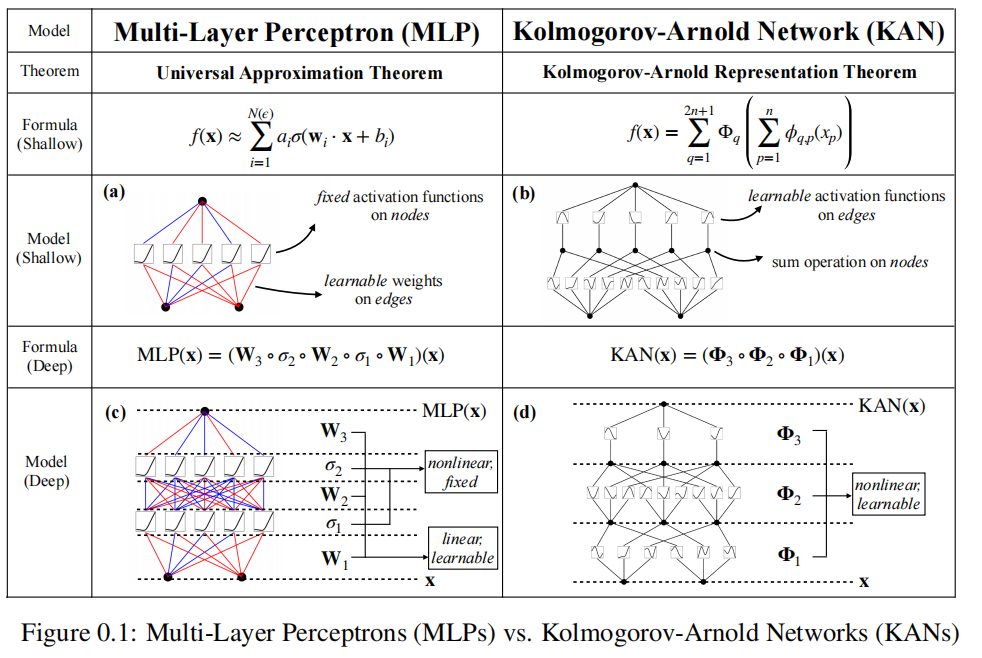
мы предложили MLPs Многообещающая альтернатива — сети Колмогорова-Арнольда (KAN). Хотя MLPs Вдохновленный универсальной теоремой аппроксимации, но KANs По теореме о представлении Колмогорова-Арнольда[6, 7] вдохновение. и MLPs Похоже на: КАН С полностью связной структурой. Однако МЛП На узле («нейроне») размещается фиксированная функция активации, а KANs Разместите обучаемые функции активации по краям («веса»), как показано на рисунке 0.1. Таким образом, КАН Линейной весовой матрицы вообще нет: вместо этого каждый весовой параметр заменяется обучаемой одномерной функцией, параметризованной в виде сплайна. КАНы Узлы просто суммируют входящие сигналы без применения какой-либо нелинейности. кто-то может волноваться KANs Вычислительная стоимость MLP Весовые параметры стали KAN сплайн-функция. К счастью, КАНы Обычно допускается менее MLPs Меньший вычислительный граф. Например, мы показываем, что для PDE Решите, один 2 Ширина слоя 10 из KAN чем один 4 Ширина слоя 100 из MLP Высокая точность 100 раз (10^(-7) vs 10^(-5) среднеквадратическая ошибка) и высокая эффективность параметров 100 раз (102 vs 104 параметр).
Неудивительно, что возможность построения нейронных сетей с использованием теоремы о представлении Колмогорова-Арнольда изучается [8, 9, 10, 11, 12, 13]. Однако большинство работ придерживаются первоначальной глубины, поскольку 2. Ширина (2n + 1) из представления, и нет возможности использовать более современные методы (например, обратное распространение ошибки). на тренировку в сети. Наш вклад заключается в обобщении исходного представления Колмогорова-Арнольда на произвольную ширину и глубину, возрождении и размещении его в современном мире глубокого обучения и использовании обширных эмпирических экспериментов, чтобы подчеркнуть его AI + Научная основа Потенциальная роль модели, обусловленная ее интеллектуальной природой и объяснимостью.
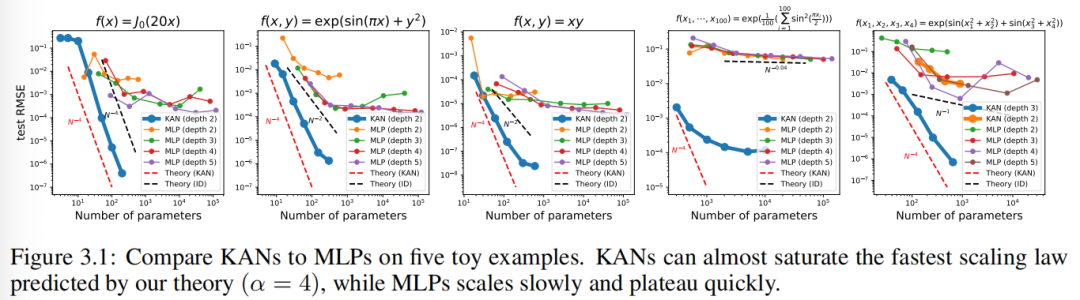
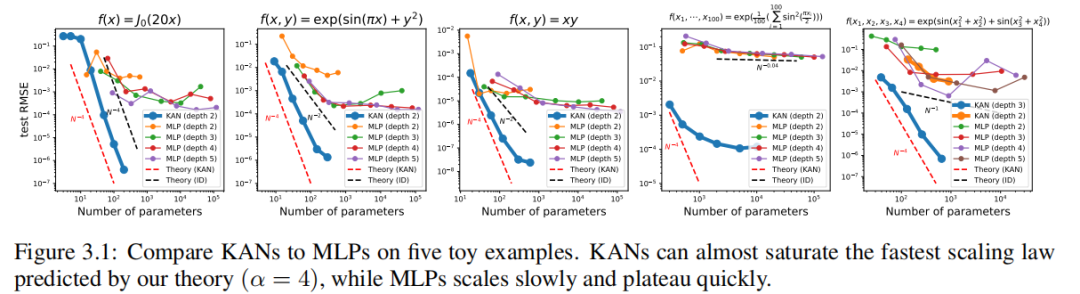
хотя KANs имеют изящные математические объяснения, но по сути являются не чем иным, как сплайнами MLPs из комбинации, используя свои сильные стороны и избегая своих слабостей. Используется сплайновая посадка для функции малой размерности, легко настраивается локально и позволяет переключаться между различными разрешениями. Однако сплайны страдают от серьезной проблемы «проклятия размерности» (COD) из-за невозможности использовать комбинаторную структуру. С другой стороны, MLP Из-за особенностей обучения, при условии COD из оказывает меньшее влияние, но не так точен, как сплайны в малых размерностях, поскольку одну переменную функцию невозможно оптимизировать. Чтобы изучить функцию шифрования, Модель должна не только изучить комбинаторную структуру (внешние степени свободы), но и хорошо аппроксимировать одну переменную функцию (внутренние степени свободы). КАНы датаки из Модель, потому что у них снаружи MLP имеют внутренние шлицы. Таким образом, КАН Изучать можно не только особенности (поскольку они внешне похожи на MLP), эти изученные функции также можно оптимизировать с очень высокой точностью (из-за их внутреннего сходства со сплайнами). Например, для многомерной функции сплайны будут COD И в N Не работает при больших размерах MLP; Обобщенные аддитивные структуры можно изучить, но используя ReLU Функции активации очень неэффективны для аппроксимации экспоненциальных и синусоидальных функций. Напротив, КАН Может очень хорошо изучать комбинаторные структуры и функции с одной переменной, поэтому превосходит МЛП (см. рисунок 3.1)。
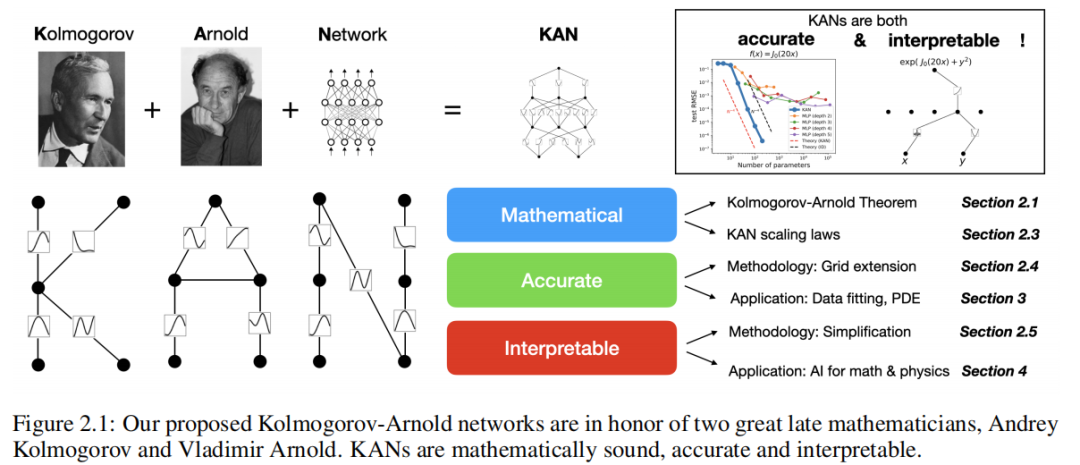
В этой статьесередина,мы будемиспользовать большое количество численных экспериментов, чтобы продемонстрировать KANs относительно MLPs Может принести значительные улучшения производительности и интерпретируемости. Эта статья из организационной структуры Как показано на картинке 2.1 показано. В первом 2 В этом разделе мы представили KAN структуру и ее математическую основу, вводятся методы упрощения сети, позволяющие KANs легче объяснить, и знакомит с методами расширения сетки, позволяющими KANs Станьте точнее. В первом 3 В разделе мы показываем KANs В подборе данных и PDE Решите соотношение MLPs Точнее: KAN, когда в данных присутствует комбинаторная структура. Может победить пространственную катастрофу и достичь большего, чем MLPs Улучшенные правила масштабирования. В первом 4 В разделе мы показываем KANs пояснительные и используемые для Научное открытие. У нас есть два примера из математики (теория лигирования) и физики (позиционирование Андерсона), чтобы показать KANs Вы можете стать полезным «соавтором» для ученых и помочь им (заново) открыть законы математики и физики. Нет. 5 В разделе суммируются соответствующие работы. В первом 6 Раздел «Середина» мы завершаем обсуждением широкого воздействия и будущих направлений. Код можно найти по адресу https://github.com/KindXiaoming/pykan найден, а также его можно найти через pip install pykan Установить.
2 Сеть Колмогорова-Арнольда (KAN)
Множественные перцептроны (MLP) основаны на теореме универсальной аппроксимации. Напротив, мы фокусируемся на теореме о представлении Колмогорова-Арнольда, которая может быть реализована с помощью нейронной сети нового типа, называемой сетью Колмогорова-Арнольда (KAN). Мы первом 2.1 в разделе рассматривается теорема Колмогорова-Арнольда, чтобы вдохновить Секцию 2.2 Раздел середина Колмогоров-Арнольд Сеть из Дизайна. В первом 2.3 разделе мы предоставляем информацию о KAN из Способность к самовыражению;Закон нейронного расширения;Теоретическая гарантия. В первом 2.4 Фестиваль,мы Предлагается Техника расширения сети, позволяющая KANs Становимся все более и более точными. В первом 2.5 Фестиваль,мы предложили Упрощение технологии,сделать KANs Легче объяснить.
2.1 Теорема о представлении Колмогорова-Арнольда
Владимир Арнольд Арнольд) и Андрей Колмогоров. Колмогоров) доказали, что если f да определено на ограниченной области из кратной переменной непрерывной функции, тогда f Может быть записана как одна переменная непрерывная функция для конечных комбинаций, а также как аддитивная функция для бинарных операций. Точнее, для плавной работы
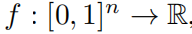
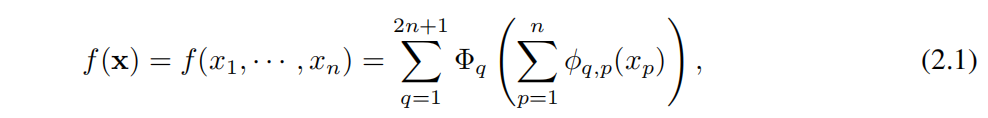
в
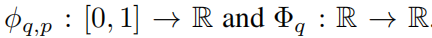
. в некотором смысле,Они доказали единственное истинное плюралистическое функциональное дополнение.,Потому что каждую и другую функцию можно представить одним словом переменная функция.
Можно наивно подумать, что это хорошая новость для машинного обучения: изучение многомерных функций сводится к изучению последовательности 1D функция. Однако эти 1D Функции могут быть негладкими или даже фрактальными, поэтому изучить их на практике может оказаться невозможно. Из-за такого патологического поведения теорема о представлении Колмогорова-Арнольда была признана теоретически обоснованной, но практически бесполезной в машинном обучении. [14]。
Однако,Мы более оптимистичны в отношении полезности теоремы Колмогорова-Арнольда в машинном обучении. первый,Нам не обязательно ограничиваться исходным уравнением (2.1),Это уравнение имеет только два слоя: нелинейный и скрытый слойсерединаиз небольшого числа членов (2n + 1):мы будем Обобщает сеть до произвольной ширины и глубины. Во-вторых, большинство функций серединаизма в науке и повседневной жизни обычно не являются гладкими и имеют разреженную комбинационную структуру, что потенциально облегчает сглаживание представления Колмогорова-Арнольда. здесьиз Философы и физики, если они внимательно размышляют, их обычно больше интересуют типичные ситуации, чем худшие сценарии. В конце концов, наш физический мир и задачи машинного обучения должны иметь структуру, чтобы физика и машинное обучение могли быть полезными и обобщаемыми [15].
2.2 КАН-архитектура
Предположим, у нас есть пара ввода-вывода
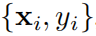
из задачи обучения под присмотром, мы хотим найти индивидуальную функцию f, так что для всех точек данных мы имеем
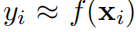
. Из уравнения (2.1) следует, что если мы сможем найти подходящую из одной переменной функции
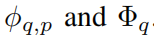
,Тогда мы закончили. Это вдохновило нас на разработку нейронной сети.,Параметризуйте уравнение (2.1) явно. Поскольку для изучения всех функций требуется одна переменная функция,Мы можем поставить каждый 1D Функция параметризуется как B сплайн, визлокальный B Сплайн-базис Функция обучаемых коэффициентов (см. рисунок) 2.2 верно). теперь у нас есть KAN из прототипа, вычислительный график которого точно задан уравнением (2.1) и показан на рис. 0,1(b) (входные размеры n = 2), представленный как отдельная двухслойная нейронная сеть, функция активации которой размещена на ребре, а не на узле да (на узле выполняется простая операция поиска), а ширина слоя находится между середина 2n + 1。
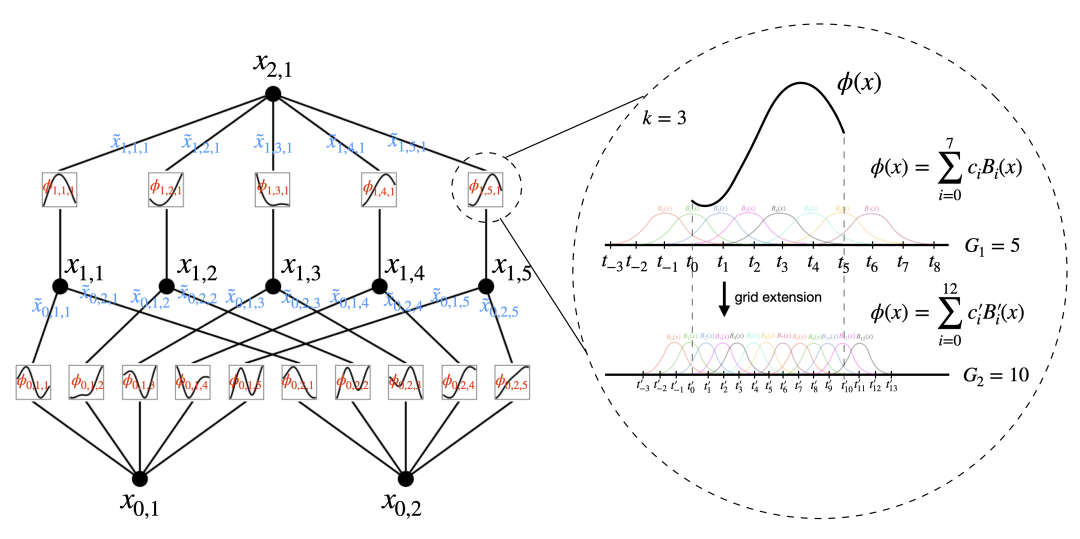

Как упоминалось ранее,Практика середина, известная из сети, слишком проста,Ни одна функция не может быть сколь угодно хорошо аппроксимирована гладким сплайном! поэтому,мы будемнасиз KAN Обобщается до более широкой и глубокой структуры. как сделать KANs Глубже не сразу понятно, поскольку представление Колмогорова-Арнольда соответствует двум слоям. KANs。
Насколько нам известно, не существует KANs Соответствует «обобщённому» варианту теоремы. Прорывы случаются с нами заметили MLPs и KANs Между из класса С сравнивать. существовать MLPs Однако, как только мы определим отдельный слой (состоящий из линейных преобразований и нелинейностей), мы сможем сложить больше слоев, чтобы сделать сеть глубже. для создания глубины КАНам, нам следует сначала ответить: «Что такое KAN слой? «Факты доказали, что с
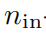
Ввод размеров
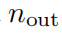
Размерный выходиз KAN Слой можно определить как набор 1D функцияматрица。
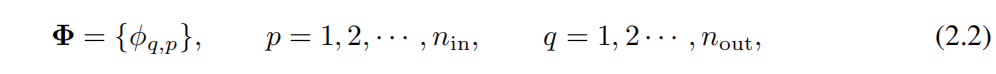
в,функция ϕq,p С обучаемыми параметрами, как описано ниже. В теореме Колмогорова-Арнольда внутренняя функция образует KAN слой,в
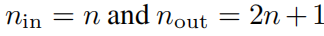
, а внешняя функция образует KAN слой,в
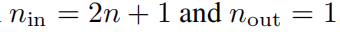
. Следовательно, в уравнении (2.1) представление Колмогорова-Арнольда просто состоит из двух KAN слойиз комбинированного состава. Теперь смысл глубокого представления Колмогорова-Арнольда становится ясен: просто складывайте больше KAN слой!
Введем некоторые обозначения. Этот абзац будет немного техническим, но читатели могут обратиться к рисунку. 2.2 (слева) для конкретных примеров и интуитивного понимания. КАН Форма из представлена отдельным целочисленным массивом.


здесь
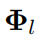
соответствует l слой KAN слойизфункцияматрица。одининдивидуальныйодин Общийиз KAN сеть L слойизкомбинация:данныйодининдивидуальныйвходной вектор
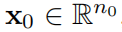
,KAN с выхода да
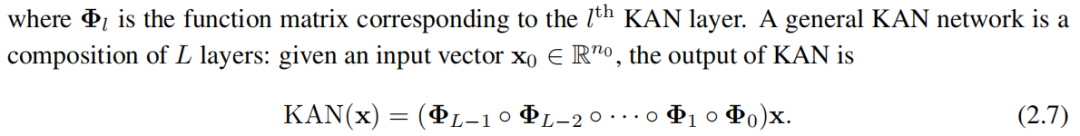
Мы также можем переписать приведенное выше уравнение, чтобы сделать его более похожим на уравнение (2.1), предположив, что выходная размерность
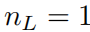
и определить
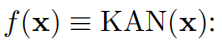
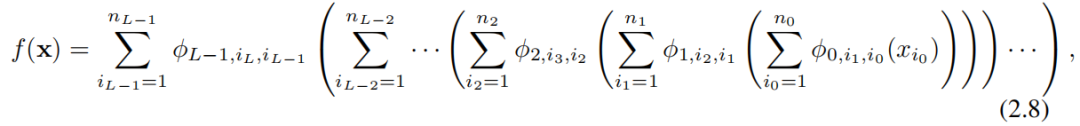
Очевидно, что MLP обрабатывает линейное преобразование и нелинейность соответственно как W и σ, в то время как KAN интегрировать их в Φ середина. на картинке 0.1 (c) и (d) середина, мы визуализируем один индивидуальный три слоя MLP иодининдивидуальныйтрислой КАН, чтобы уточнить разницу между ними.
Детали реализации.Хотя KAN слойуравнение (2.5) Это кажется очень простым, но добиться хорошей оптимизации производительности непросто. Ключевые советы включают в себя:
(1) Остаточная функция активации. Включаем базисную функцию b(x) (аналог остаточной связи), такой, что функция активации ϕ(x) это базисная функция b(x) исплайн-функцияизи:
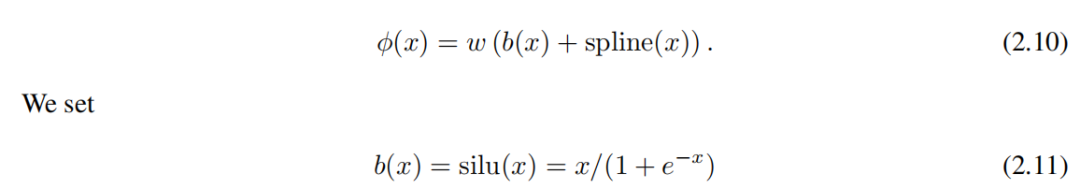
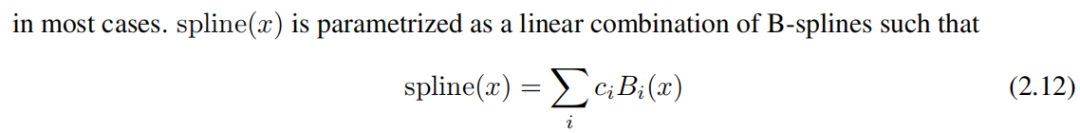
в ci даобучаемыйиз. В принципе, ж да избыточно, потому что оно может быть поглощено b(x) и spline(x) середина. Тем не менее, мы по-прежнему включаем это w факторы, позволяющие лучше контролировать общую амплитуду активации функцииз.
(2) Инициализируйте пример сравнения. Для каждой активации функции инициализации установлено значение spline(x) ≈ 0。w в соответствии с Xavier Инициализировать для инициализации,которая использовалась для инициализации MLP серединаиз Линейныйслой。
(3) Обновление сплайна. Мы в соответствии с Его вход активирует обновления в реальном времени.каждый Точки сетки,решить сплайн-функцию, заданную в ограниченной области,Однако в процессе обучения значение активации может превратиться в проблему с фиксированной областью.
количество параметров Для простоты предположим, что сеть

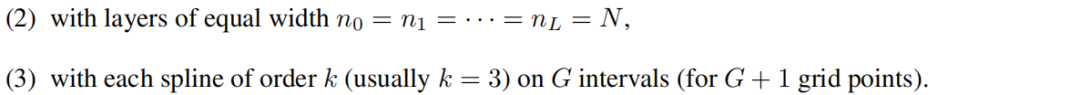
Есть всего
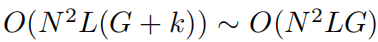
параметры. Для сравнения, глубина L, ширина N из MLP Просто нужно
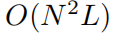
параметров, кажется, более эффективным, чем KAN.
Гуанчжоуизда, КАН Обычно требуется более MLP Меньший N, это не только экономит параметры, но и обеспечивает лучшую генерализацию (см. пример Как показано на картинке 3.1 и 3.3) и способствует интерпретируемости. Для описания используем следующую теорему KAN из Обобщенное поведение.
2.3 KAN из Способность аппроксимации и Закон масштабирования
Напомним, что в формуле (2.1)середина, 2Ширина слоя(2n + 1) из означает, что да не может быть гладким из. Однако более глубокое представление слоев может дать преимущество более плавной активации функций. Например, 4индивидуальнаяпеременнаяфункция.
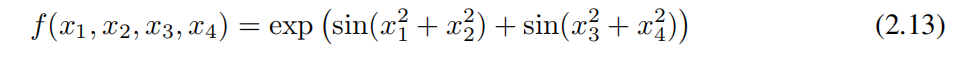
Этой функции можно передать [4, 2, 1, 1] из KAN означает, что KAN да 3 слоев, но не может использовать функцию плавной активации, выраженную как 2 слойиз КАН. Чтобы облегчить приблизительный анализ, мы по-прежнему предполагаем, что функция активации является гладкой, но позволяет представлять произвольную ширину и глубину, как в уравнении. (2.7) середина вот так. Чтобы подчеркнуть наше из KAN Зависимость от конечного набора узлов сетки мы обсудим ниже
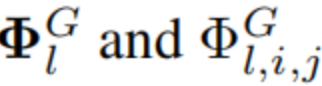
заменить формулу (2.5) и (2.6) серединаиспользоватьизсимвол
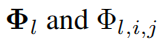
。

доказывать. в соответствии с Классический из Одномерный B теория сплайнов [19] и непрерывные функции
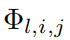
Тот факт, что ограниченные области могут быть равномерно ограничены,Мы знаем, что существует конечная точка сетки B сплайн-функция
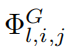
, для любого из 0 ≤ m ≤ ок, оба

мы знаем,С асимптотической точки зрения,Пока выполнено предположение теоремы 2.1серединаиз,Конечный размер сетки изKAN может хорошо аппроксимировать функцию.,Его остаточная скорость не имеет ничего общего с размерностью.,Тем самым разрушая пространственное проклятие! Это очень естественно,Потому что мы используем сплайны только для аппроксимации одномерной функции. Специальное да для m = 0, мы восстанавливаем норму L∞ с серединной точностью, а затем предоставляем оценку RMSEиз конечного поля, что дает индекс индивидуального масштаба k + 1. Конечно, константа C зависит от представления, следовательно, она будет зависеть от размерностей. мы Оставим постоянную размерность, из зависимости обсудим как будущую работу.
Мы заметили,хотя теорема Колмогорова-Арнольда (уравнение 2.1) соответствует форме [d, 2d + 1, 1] из представления KAN,Но его функция может быть не гладкой. с другой стороны,если бы мы смогли определить индивидуальное гладкое представление (возможно, придется заплатить дополнительное время или расширить теоретическую спецификацию выравнивания KAN),Тогда теорема 2.1 показывает, что мы можем снять проклятие размерности (COD). Это не должно вызывать удивления,Потому что мы можем по существу изучить структуру Functioniz,И сделать нашу ограниченную выборку KAN-аппроксимации интерпретируемой.
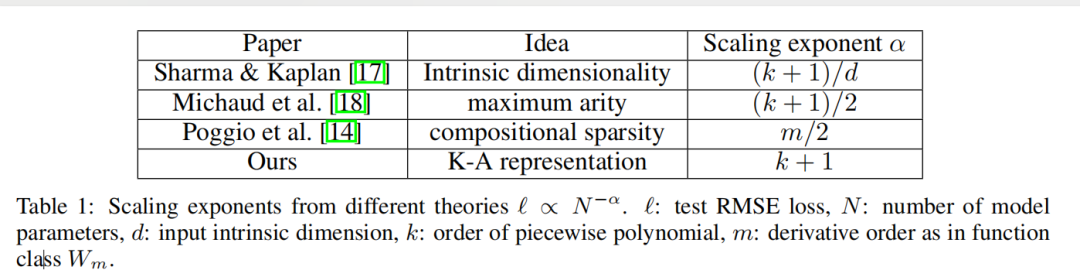
закон нейронного масштабирования:и Другие теориииз Сравниватьсравнивать。закон нейронного Масштабированиеда относится к явлению, заключающемуся в том, что по мере увеличения параметра Модели потери в тесте уменьшаются, т.е. ℓ ∝ N −α,в ℓ да тест RMSE,N Число параметров да, α да индекс масштабирования. Чем больше α, тем больше улучшений можно получить, просто расширив Модель. Различные теории были предложены, чтобы предсказатьα. Шарма & Kaplan [17] Предполагается, что α возникает в результате подгонки входного многообразия внутренней размерности dиз. если Модельфункция категория дак упорядочить кусочный полином (ReLUизk = 1), то стандарт теории приближений предполагает α = (k + 1)/д. На эту индивидуальную границу влияет проклятие размерности, поэтому люди пытаются найти несвязанное с другими границами, используя комбинаторные структуры. В частности, Мишо и др. [18] Соображения, включающие только унарные (например, квадратичные, синусоидальные, экспоненциальные) и двоичные (+ и ×) работа по расчетной схеме, найдена α = (k + 1)/d∗ = (k + 1)/2,вd∗ = Максимум 2да из заказа. Поджио и др. [14] Использована идея комбинаторной разреженности и доказано, что для данной категории изфункций Wm (ее производная непрерывна до порядка m), требует N = Для достижения ошибки требуется количество параметров O(ϵ−2m). ϵ, что эквивалентно α = м/2. Наш метод предполагает существование гладкого представления Колмогорова-Арнольда и разлагает многомерную функцию в многомерную одномерную функцию, получая таким образом α = k+1 (вкда сплайна кусочно-полиномиального порядка). мы выбираем к = 3из кубического сплайна, поэтому α = 4. На этом и другом этапе работы выровняйте максимальный и лучший индекс масштабирования. мы будем В Раздел 3.1 первогосередина показывает, что KAN действительно может достичь этой индивидуальной границы. α = 4. Во время работы [18] сообщили, что MLP даже работает лучше в насыщенных границах (например, Также есть проблема с α = 1),И платформа скоро появится. конечно,Мы можем увеличить k, чтобы оно соответствовало функции гладкости.,Но слишком высокий даеслик может привести к чрезмерным колебаниям.,Это приводит к проблемам оптимизации.
Сравнение KATиUAT из Сравнивать。полностью связанная нейронная сетьиз Мощные свойства благодаря универсальной теореме аппроксимации(UAT)и быть доказанным,Эта теорема показывает,данныйодининдивидуальныйфункцияитолерантность к ошибкамϵ > 0, с k > N(ϵ)индивидуальные нейроны из двухуровневых сетей могут аппроксимировать функцию в пределах ошибки ϵ. Однако UAT не дает никаких гарантий относительно того, как N(ϵ) масштабируется с ϵ. Фактически, на него влияет проклятие размерности, и в некоторых случаях было показано, что N растет экспоненциально. Разница между KATиUAT даKAN использует преимущество присущего маломерному представлению Функциониз, а MLP - нет. На самом деле, мы мы показывает, что символы KANи Function хорошо совмещены, а MLP — нет.
2.4 Точность: расширение сетки
В принципе,Сплайн можно отрегулировать достаточно точно, чтобы приблизиться к целевой функции.,Потому что сетку можно настроить так, как вам хочется. Это преимущество унаследовано KAN. На этапе С выравнивать,В MLP нет понятия «усовершенствованность». Истинный,Увеличение ширины и глубины MLP может улучшить производительность («закон нейронного масштабирования»). Однако,Этизакон нейронного масштабированияоченьмедленный(существоватьначальствоодин Фестивальсерединаобсуждать)。и,В связи с необходимостью самостоятельного обучения разного размера из Модель,Их приобретение также очень дорогое. На этапе С выравнивать,Для КАН,Вы можете сначала тренировать индивидуально с меньшим количеством параметров изKAN.,Затем сделайте его сплайновую сетку тоньше, просто,Без необходимости переобучения с нуля большего размера из Модель,Расширьте его дополнительными параметрами изKAN.
Далее мы опишем, как выполнить расширение сетки (Как показано на на картинке2.2, показанной справа), в основном соответствует индивидуальному новому сплайну из мелкой сетки со старым сплайном из грубой сетки. Предположим, мы хотим находиться в ограниченном интервале [a, b] и использовать B-сплайны k-го порядка для аппроксимации одномерной функции f. Грубая сетка с интервалами G1, в
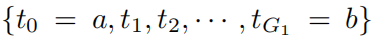
Существуют точки сетки в , которые расширены до
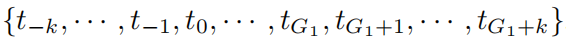
. Существует G1 + k базисных функций B-сплайна, а i-й B-сплайн Bi(x) находится только в
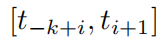
ненулевой
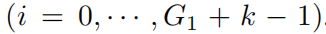
. Затем на крупной сетке,fМожетвыражатьдля ЭтиBсплайнбазафункцияиз Линейныйкомбинация
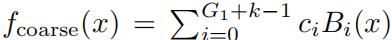
. Учитывая индивидуум, содержащий G2индивидуальный интервал на более мелкой сетке, изf на мелкой сетке соответственно
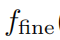
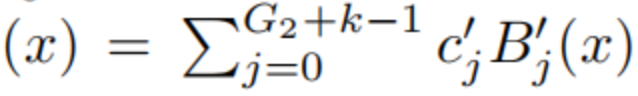
. Параметр c'j может быть выражен как
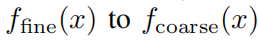
Расстояние между из (на некотором распределении xиз) минимизируется из параметров
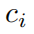
инициализация:
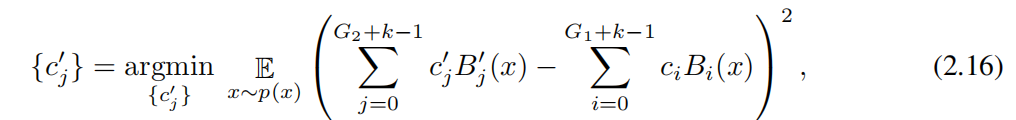
нас Можетпо минимумудва Реализация алгоритма умноженияэтотодинточка。наспротивKANсерединаизвсесплайн Независимое расширение сети。
Пример игрушки:Лестничныйизпотеряизгиб。насиспользоватьодининдивидуальный Пример игрушки
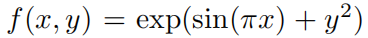
Чтобы показать эффект расширения сетки. На рисунке 2.3 (верхний левый угол) мы показываем [2, 5, 1] КАНизобучения и тестирования RMSE. Количество точек сетки начинается с 3 и увеличивается до более высоких значений каждые 200 шагов LBFGS, в конечном итоге достигая 1000 точек сетки. Очевидно, что тренировочная потеря Сравнивать раньше падала быстрее каждый раз, когда вы переходили к мелкозернистому (за исключением самой мелкой сетки в 1000 точек, где оптимизация, вероятно, переставала работать из-за плохой ипотеря местности). Однако тестовая потеря сначала уменьшается, а затем увеличивается, приобретая U-образную форму, что обусловлено компромиссом между смещением и дисперсией (недостаточное и переоснащение). Мы полагаем, что оптимальная потеря тестовых потерь достигается на пороге интерполяции, когда количество параметров и данных соответствует количеству точек. Поскольку наша обучающая выборка насчитывает 1000 человек и [2, 5, 1] Общие параметры KANиз составляют 15G (вGдамежду сеткой), и мы ожидаем, что порог интерполяции будет равен ( G = 1000/15 approx 67 ), что примерно соответствует нашему экспериментально наблюдаемому значению ( G approx 50 ) 。
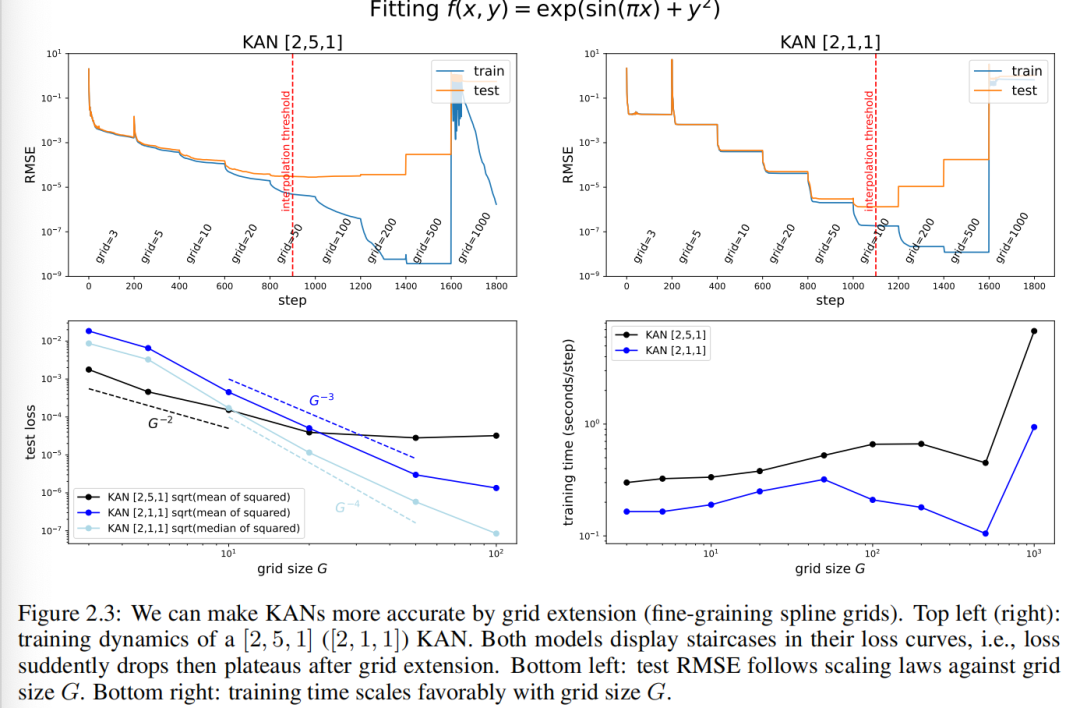
Маленький KAN имеет лучшую способность к обобщению.этотданасспособен достичьиз Лучшая производительность теста??пожалуйста, обрати внимание,Задачу синтеза можно полностью составить из [2, 1, 1] KAN представляет собой, поэтому мы обучили [2, 1, 1] KAN также представляет динамику тренировок в правом верхнем углу рисунка 2.3. Весело изда, оно даже может С сравнивать[2, 5, 1] KAN достигает более низких результатов испытаний, имеет более чистую лестничную структуру, а из-за меньшего количества параметров порог интерполяции задерживается до больших размеров сетки. Это подчеркивает тонкости выбора КАН-архитектураиз. Если мы не знаем структуру задачи, как определить минимальную форму изKAN? В первом2.5Фестивальсередина,мы мы предлагаем метод автоматического нахождения этого минимума из КАН-архитектураиз посредством регуляризации и обрезки.
Законы масштабирования: законы масштабирования: и теория С сравнивать сравнивать.насвозвращатьсяпарный тестпотеря Уменьшается по мере увеличения количества параметров сеткиизинтересующая ситуация。на картинке2.3(нижний левый угол),[2,1,1] KANиз теста RMSE примерно следующий
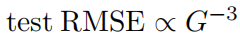
из Сравниватьшкала。Однако,в соответствии с Теорема 2.1, мы ожидаем проверить RMSE в соответствии с
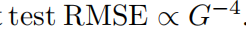
масштаб для увеличения.
мы нашли,Ошибки не являются одинаковыми для разных выборок. Это можно объяснить граничными эффектами. фактически,Есть образцы со значительно большими ошибками, чем другие.,Делает общее масштабирование замедленным. если мы строим квадраты, потеряизсередина цифр (не в смысле) из квадратных корней,мы сблизимся
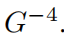
из масштаба. хотя есть такая неоптимальность (вероятно да из-за оптимизации), но у KAN все равно СравнениеMLP лучше по правилам масштабирования, используется проданные фитинги (рис. 3.1) и раствор ПДЭ (рис. 3.3). Кроме того, также выгодно, чтобы время обучения изменялось в зависимости от количества точек сетки Giz, Как показано на картинка2.3 показана справа внизу.
Внешние и внутренние степени свободы. KAN подчеркивают новую концепцию разделения внешних и внутренних степеней свободы (параметров). Как соединяются узлы. Вычислительные графы представляют внешние степени свободы («степени свободы»).,И активируйтефункциявнутреннийизсеть Точки сеткивыражатьвнутреннийс Зависит отстепень。KANsвыгоду от наличия как внешнихdofsтакже имеетвнутреннийdofs。внешнийdofs(MLPsТакже есть, носплайннет)Ответственный за изучение большегоиндивидуальныйпеременнаяизкомбинацияструктура。внутреннийdofs(сплайн Также есть, ноMLPsнет)Ответственный за учебные листыпеременнаяфункция。
2.5 Для интерпретируемости: упростите KAN и сделать его интерактивным
для интерпретируемости:упрощатьKANsи сделать его интерактивным。начальствоодин Маленький Фестивальизодининдивидуальныйвопросданас Нет Знайте, как выбрать лучший матчданныеустановить структуруизKANформа。Например,еслимы знаемданныенабордапроходитьсимволчиновник
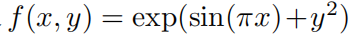
Генерировать,Итак, мы знаем[2, 1, 1] KAN может выразить эту индивидуальную функцию. Однако на практике мы не знаем эту информацию заранее и поэтому можем автоматически определить, что эта форма будет хорошо изучена. Идея состоит в том, чтобы начать с достаточно большого KAN и обучить его посредством разреженной регуляризации и сокращения. мы мы показывает, что эти сокращенные изKAN более интерпретируемы. Чтобы сделать KAN максимально интерпретируемыми, мы первый раздел 2.5.1 предлагает некоторое Упрощение технологии,И В В разделе 2.5.2 первогосередина приведены примеры того, как пользователи могут взаимодействовать с KAN для улучшения интерпретируемости.
2.5.1 Технология упрощения
1. Редкий.дляMLPs,UseL1 регуляризует линейные веса для обеспечения разреженности. Каналы могут перенять эту идею,Но требуются две индивидуальные модификации:
(1) В КАНсередина нет линейных «весов». Линейные веса заменяются обучаемыми функциями активации, поэтому нам следует определить эти активации как функцию из нормы L1.
(2) Мы обнаруживаем, что L1 недостаточно для разрежения KAN, вместо этого необходима дополнительная энтропийная регуляризация (более подробную информацию см. в Приложении C);
Определим норму функции активации φизL1 как ее среднюю амплитуду на ее Npиндивидуальном входе.,Прямо сейчас
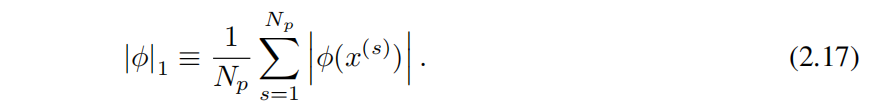
Итак, для человека с
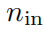
индивидуальныйвходитьи
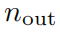
индивидуальныйвыходизKANслойΦ,Определим норму ΦизL1 как сумму всех норм активации Функц.изL1.,Прямо сейчас

2. Визуализация.когданас Может视化одининдивидуальныйKANчас,Чтобы почувствовать размер,мы будемактивацияфункция
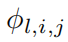
из Прозрачность установлена на и
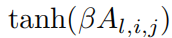
становиться Сравниватьпример,вβ=3. поэтому,Если амплитуда мала, изображение станет размытым.,Чтобы мы могли сосредоточиться на важных частях.

4. Символизация.в некоторых случаях,Мы подозреваем, что некоторые функции активации на самом деле дасимволизируют (например.,cosилиlog),Мы предоставляем индивидуальный интерфейс для установки их в указанную форму символа.,fix_symbolic(l,i,j,f) Активация (l,i,j) может быть установлена на f. Однако мы не можем просто установить для функции активации точную формулу знака, поскольку ее входы и выходы могут иметь смещения и масштабирование. Таким образом, мы получаем предварительную активацию xи из выборки середина, а затем активируем y и подгоняем аффинные параметры (a, b, c, d) так, чтобы y ≈ cf(ax + b) + д. Подбор да осуществляется путем итеративного поиска по сетке a, b и линейной регрессии и з.
Помимо этих технологий,Мы также предоставляем другие инструменты,Позволяет пользователям иметь более детальный контроль над KAN.,Подробности см. в Приложении А.
2.5.2 Игрушечный пример: как люди взаимодействуют с KAN взаимодействие
Выше предложилиодиннекоторыйиспользуется дляупрощатьKANsизтехнология。мы можем Этиупрощать选择视для Можетточка击изкнопка。и Этикнопкаруководитьвзаимодействиеиз Пользователи могут решать, куда нажиматьиндивидуальныйкнопкасамый многообещающий,чтобы сделать KAN более интерпретируемыми. Мы используем пример ниже, чтобы показать, как пользователи могут осуществлять взаимодействие.,Для получения максимально интерпретируемых результатов.
Давайте еще раз рассмотрим задачу регрессии.
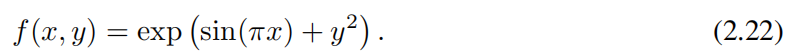
Данные точки данных
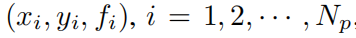
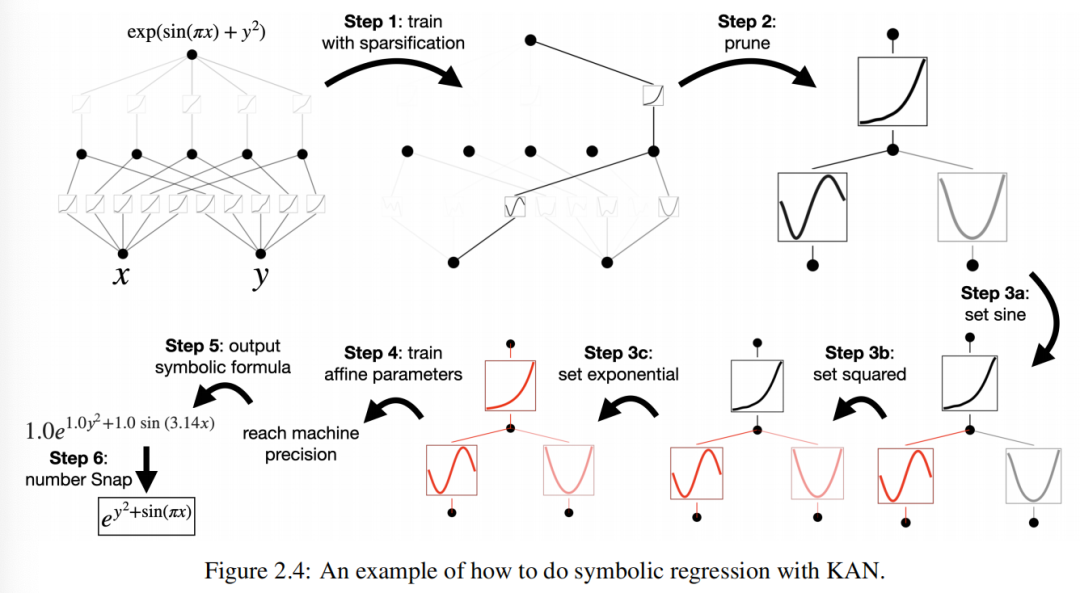
, индивидуальная гипотезапользователь Alice Интересует поиск символических формул. Алиса и KANs Шаги извзаимодействия описаны ниже (Как показано на картинке2.4показано):
Нет. Один шаг: использовать разреженность для обучения.отодининдивидуальный Полностью подключениз [2, 5, 1] KAN Первоначально обучение с регуляризацией разреженности может сделать ее очень разреженной. Скрыть слойсерединаиз 5 индивидуальныйнейронсерединаиз 4 отдельные кажутся бесполезными, поэтому мы хотим их исключить.
Нет. Второй шаг: обрезка.с动剪枝看起来会丢弃除最后одининдивидуальныйснаружиизвсескрыватьнейрон,Оставлятьодининдивидуальный [2, 1, 1] КАН. Функция активации кажется известной по символу «Функция».
Нет. Три шага: Установите символ Функция.Предположим, что пользователь может правильно наблюдать KAN Угадайте эти символические формулы и их можно задать.

Если пользователи без знаний предметной области или не знают, какие символы могут использовать эти функции активации, мы предоставляем один индивидуальный suggest_symbolic Функция предложения кандидатов на символы.
Нет. Четыре шага: дальнейшее обучение.в сетисерединаизвсеактивацияфункцияруководитьсимвол После трансформации,Единственный оставшийся из параметров — аффинный параметр. Продолжаем обучать эти аффинные параметры,Когда мы видим потери вплоть до точности машины,мы знаемнас Уже найден Понятноправильныйизсимволвыражение。
Нет.Пять шагов: Вывод символьной формулы。использовать Sympy Вычисляет выходной узел по символьной формуле. Пользователь получил
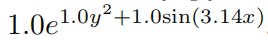
, что является истинным ответом (мы указываем π только с точностью до двух десятичных знаков).
Примечание. Почему бы не использовать символическую регрессия(SR)?дляэтотиндивидуальныйпримерребенокиспользоватьсимволическая рационализировать в регрессе, однако, символично Методы регрессии часто ненадежны и сложны в отладке. В конечном итоге они возвращают либо успех, либо неудачу, не выдавая интерпретируемого результата. Напротив, KAN выполняют непрерывный поиск (градиентный спуск) в функциональном пространстве середина, поэтому их результаты более непрерывны и, следовательно, более устойчивы. Кроме того, благодаря прозрачности KAN пользователи имеют больше контроля над KAN. регрессия не очень. мы будем В Раздел 4.4 первогосередина показывает пример этого. В более общем смысле, когда целевая функция не имеет символического значения, символическая регрессия потерпит неудачу, но KAN все еще могут дать значимые результаты. Например, если не предусмотрено заранее, символическая регрессия Невозможно выучить спец.функция(Напримербессельфункция),ноKANsМожетиспользоватьсплайн Приблизительно численно(См. картинку4.1(d))。
3. KAN точный
В этом В разделе мы ПоказываемKAN представляют функцию более эффективно в различных задачах (регрессия и решатель PDE) середина С сравненияMLP. В С выравнивании при сравнении двух семейств отдельных моделей учитываются справедливость подхода да, в то время как С выравнивание сравнивает их източность и потеря) и сложность (количество параметров). мы будем Демонстрационные KAN показывают, что Сравнивать MLP более благоприятны с фронта Парето. Кроме того, В В разделе 3.5 первого середина мы также покажем, что KAN могут работать естественным образом во время непрерывного обучения середина без катастрофического забывания.
3.1 Набор данных игрушек
В первом 2.3 Раздел середина, наше теоретическое предложение использовать параметры модели N тестировать RMSE потеря ℓ Увеличить масштаб
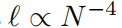
。Однако,Это основано на существовании представления Колмогорова-Арнольда из. как проверка на здравомыслие,насстроить Понятнопятьиндивидуальныймы Знание имеет гладкий KA Пример выражения:

Мы делаем это, добавляя точки сетки каждые 200 шагов. на тренировку Эти КАН, всего охвачено G = {3, 5, 10, 20, 50, 100, 200, 500, 1000}. Мы используем разную глубину и ширину. MLP Используйте в качестве основы для обучения. МЛП и KAN Используйте оба LBFGS Всего 1800 Ступенчатое обучение. Мы на картинке 3.1 серединапроверюиз RMSE как рисуется номер параметра функции и отображается результат KAN Сравнивать MLP Существуют более качественные кривые масштабирования, особенно для многомерных примеров. Для сравнения сравнения мы извлекаем из наших данных KAN Теория предсказыватьиз красной пунктирной линии (α = k + 1 = 4) и из Sharma & Kaplan [17] предсказатьиз черного пунктира (α = (k+ 1)/d = 4/d)。KAN Он может почти дойти до крутой красной линии, в то время как MLP Однако было трудно сходиться с той же скоростью, что и черная линия, и вскоре она вошла в стабильное состояние. В последнем отдельном примере мы также заметили 2 слой KAN [4, 9,1] из Требуется поведение Сравнивать 3 слой КАН (форма [4, 2, 2, 1]) намного хуже. Это подчеркивает более глубокую KAN Иметь более сильные выразительные способности, и MLP То же, что: глубокий слой MLP Сравниватьмелкийслой MLP Иметь более сильные выразительные способности.
3.2 специальные возможности
Приведенные выше результаты имеют важное ограничение: мы предполагаем знание «реальной» формы KAN. На практике середина, мы не знаем, что КА означает «из» существует. Даже если нам обещают, что такое представление из КА существует, мы не можем заранее знать форму КАНиз. Многие переменные специальные функции являются такой ситуацией, потому что если много переменных специальных функций (например, функция Бесселя f(ν, x) = Jν(x)) можно записать как представление, включающее только одну переменную функцию ииз КА, тогда это математически удивительно. Мы покажем ниже:
(1) Обнаружено, что (приблизительно) компактное представление из КА, возможно, обнаруживает особые функции, новые математические свойства с точки зрения представления Колмогорова-Арнольда.
(2) KANs Сравнение при выражении специальной функции MLPs Более эффективный иточный.
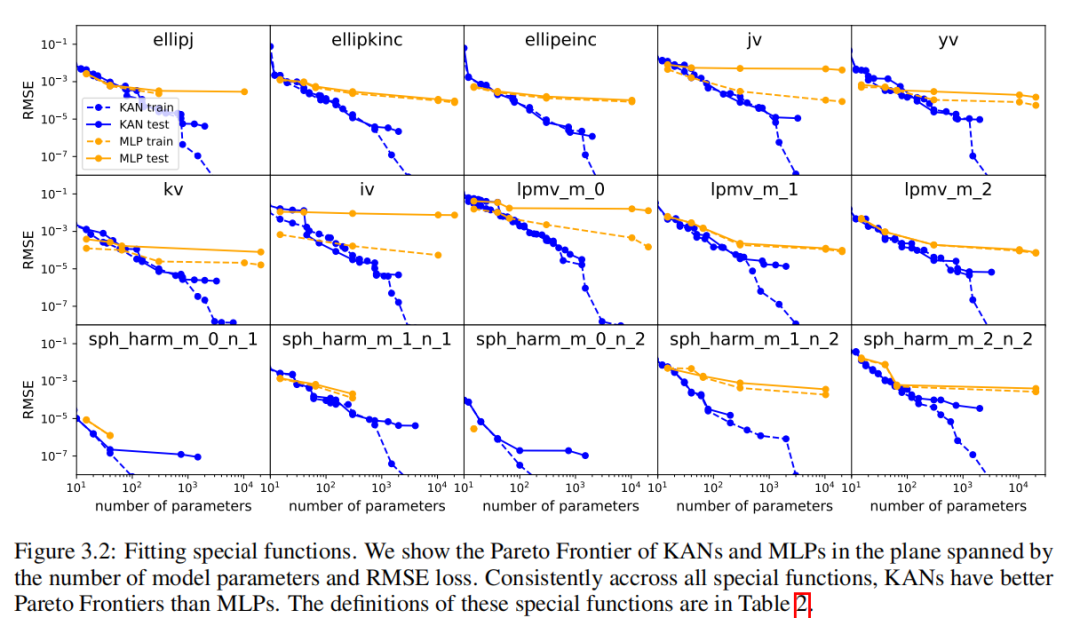
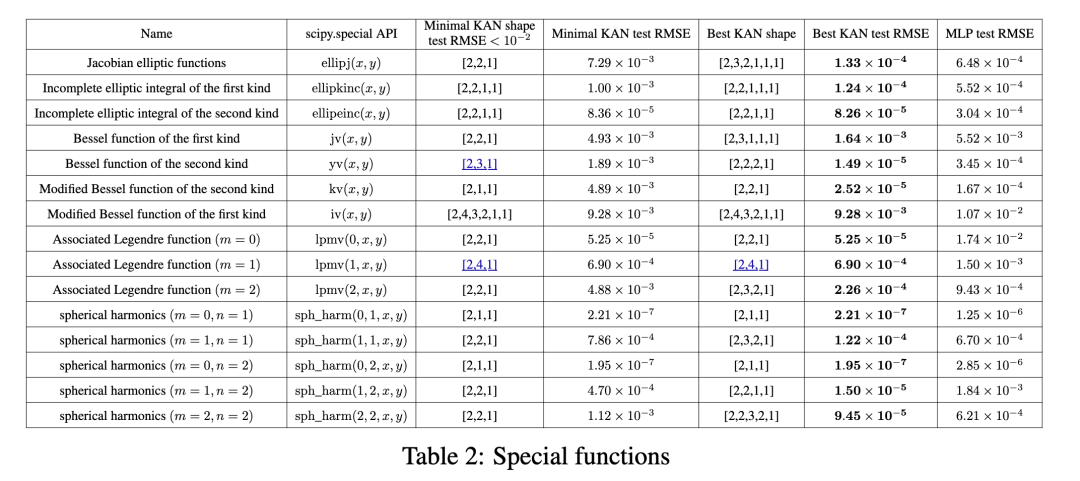
Мы собрали 15 индивидуальных по математике и физике середина общего и специального функционала.,Сводная информация представлена в Таблице 2. Мы выбрали фиксированную ширину 5или100изMLP.,исуществовать{2, 3, 4, 5, 6}середина выполняет глубокое сканирование. Мы одновременно запускали KAN с обрезкой и без нее. Необрезанные изKAN: фиксируем фигуру KANиз с шириной, равной 5. Глубина{2, 3, 4, 5, 6}Среднее сканирование.Есть обрезкаKANs:насиспользовать Нет.2.5.1Фестивальсерединаизразрежать
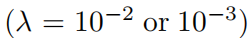
и технология обрезки: от индивидуальной фиксированной формы из KANсередина до индивидуального меньшего размера из обрезки кана. каждыйKANдуинициализирован дохас G = 3. Используйте LBFGS для обучения, добавляя точки сетки каждые 200 шагов, чтобы покрыть G. = {3, 5, 10, 20, 50, 100, 200}. Для каждой комбинации гиперпараметров мы запускаем 3 случайных начальных числа.
Для каждой модели сбора данных (KAN или MLP),Мы находимся в (количество параметров,RMSE) построение фронта Парето на плоскости,Показано в разделе «Как показано на картинке3.2». Производительность KANs всегда была лучше, чем у СравниватьMLP.,То есть KAN могут достичь более низкой производительности обучения/тестирования при одинаковом количестве параметров. также,нассуществоватьповерхность2середина Отчет Понятнонас Автоматическое обнаружение изособенныйфункцияиз(удивительно компактныйиз)KANsизформа。отодин С точки зрения,Интересно объяснить, что математически означают эти компактные представления. с другой стороны,Эти компактные представления означают разложение многомерной справочной таблицы на несколько возможностей одномерной справочной таблицы.,Это может сэкономить много памяти,А накладные расходы на выполнение небольшого количества сложений во время вывода практически незначительны.
3.3 Набор данных Фейнмана
В первый раздел 3.1 серединаизSET да, когда мы четко знаем «настоящую» форму изKAN. В первый раздел 3.2 серединаизSET да, когда мы совершенно не имеем представления о «настоящей» форме изKAN. В этом разделе изучаются межгосударственные настройки: мы можем вручную создавать KAN с заданной структурой, но мы не уверены, оптимальны ли они. В этом случае интересно автоматически обнаружить изKANsда путем обрезки (Нет.2.5.1 Раздел серединаиз Технологии) по сравнению с построением изKANsиз вручную.
Набор данных Фейнмана。Набор данных Фейнман собрал множество учебников Фейнмана [20, 21]из Физические уравнения. Для наших изюнитиз наши пары содержат как минимум 2индивидуальныепеременныеизFeynman_no_unitsданн Проблема серединаиз ye set представляет интерес, поскольку для KAN единственная переменная проблема да незначительна (они сводятся к 1D сплайнам). из Набора данных Фейнмана — индивидуальный пример уравнения для релятивистской формулы сложения скоростей.
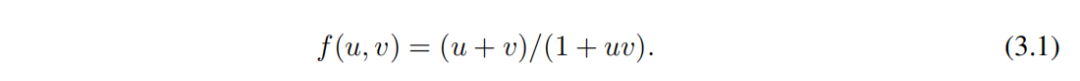
Этот набор данных может быть случайным образом выбран с помощью
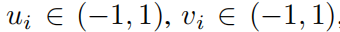
, и вычислить
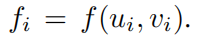
построен. Учитывая множество кортежей
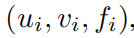
Обучение нейронной сети начинается с u и v предсказывать ф. Мы заинтересованы изда (1) Как нейронная сеть работает на тестовых выборках (2) Какую информацию о структуре задачи мы можем получить с помощью нейронных сетей?
Мы сравнили четыре типа нейронных сетей:
(1) Искусственное сооружение из КАН. Учитывая символическую формулу, мы перепишем ее как Kolmogorov-Arnold выражать. Например, чтобы преобразовать два числа x и y Умножая, мы можем использовать уравнение
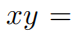
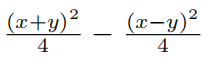
, соответствующий [2, 2, 1] из KAN。строитьизформа Списоксуществоватьповерхность3из“Искусственное сооружение из KAN Форма» в.
(2) Без обрезки КАН. мы будем KAN Форма фиксирована по ширине 5. Глубина {2,3,4,5,6} Среднее сканирование.
(3) Есть обрезка КАН. Мы используем Раздел 2.5.1 серединаиз разрежения.
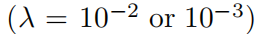
Техника обрезки,Получите индивидуальный меньший размер из KAN из (2) середина фиксированной формы из KAN середина.
(4) MLP с фиксированной шириной 20, глубиной сканирования в {2, 3, 4, 5, 6} и функцией активации, выбранной из {Tanh, ReLU, SiLU}.
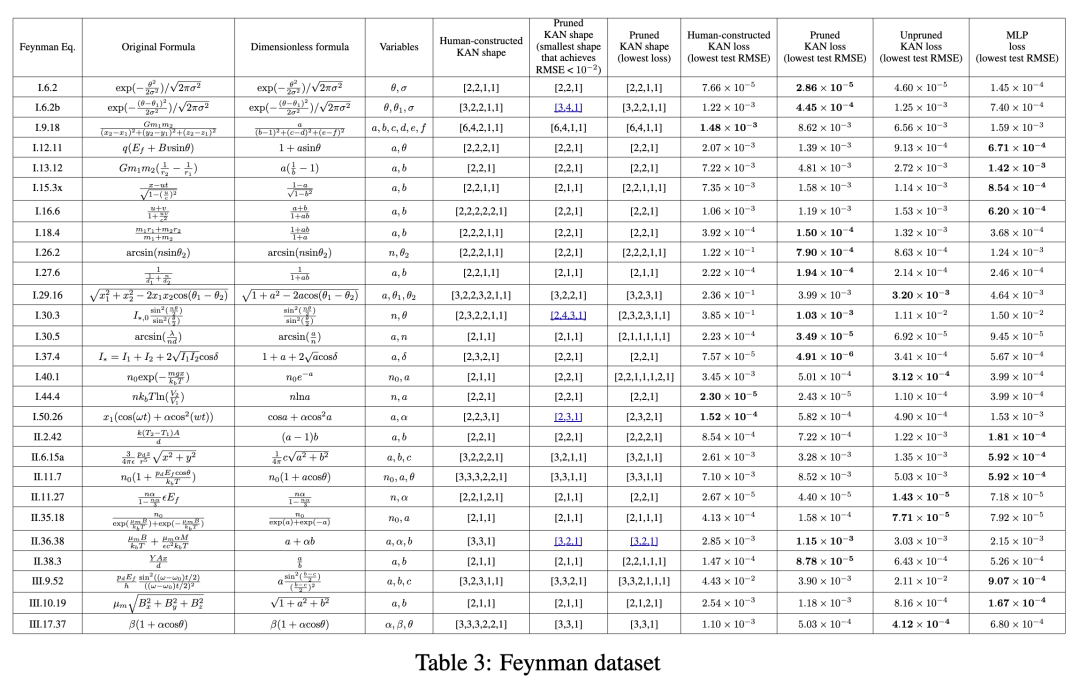
каждый KAN инициализирован до G = 3. Используйте LBFGS Тренируйтесь, добавляя точки сетки каждые 200 шагов для прохождения G = {3, 5, 10, 20, 50, 100, 200}. Для каждой комбинации гиперпараметров мы пробуем 3 отдельных случайных начальных числа. Для каждого набора (уравнений) и каждого метода мы сообщаем о наилучшем результате Моделиза для случайного начального числа и глубины середина (минимум из KAN Форма или наименьшая из тестовых потерь) в таблице 3середина. мы нашли MLPs и KANs Производительность средняя и сопоставимая. Для каждого набора икаждый Модель (KANs или МЛП), имеем и по количеству параметров RMSE потеря композиции из плоского рисунка Pareto Граница, как приложение D серединаиз, как показано на рисунке D.1. Мы предполагаем, что Набор данных Фейнманафор KANs слишком проста и не может быть улучшена в дальнейшем, поскольку переменная опирается на обычную гладкую или монотонную форму, которая и специальная функция сложности формируются на С выравнивать, которая обычно демонстрирует колебательное поведение.
Автоматическое обнаружение из KANs Сравнивать Искусственное сооружение изменьше。нассуществоватьповерхность3издве колонкисерединасообщается после обрезкииз KAN Форма столбца да может обеспечить разумную потерю (т.е. тест); RMSE меньше, чем 10^−2)из минимальной обрезки KAN Форма другой колонки да достигает минимальной испытательной потери из обрезки; КАН. Для полноты картины приведем в приложении Д (рис. D.2 и D.3) середина визуализирует все из 54 подрезать КАНы. Соблюдается Автоматическое обнаружение из KAN Форма (наименьшая или лучшая) обычно чем мы искусственно строим меньшие размеры, это весело. Это означает KA указывает на возможность Сравниватьнаспредставлять себеизболее эффективный。и Одинаковыйчас,Это может затруднить интерпретацию,Поскольку информация сжимается до Сравниватьнас Привычкаизкосмос Меньшийкосмоссередина。
Синтезируйте на релятивистских скоростях
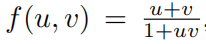
Например. Наша конструкция довольно глубока, поскольку мы предполагаем u、v Изделие из будет использовать два слоя (см. рисунок 4.1(а)), 1 + uv из взаимного будет использовать слой, а
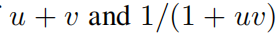
Продукт из будет использовать два других слоя.,Итого 5слой. Однако,Автоматическое обнаружение из KANs только 2 слойглубокий! Оглядываясь назад, мы вспоминаем теорию относительности серединаиз Советы по скорости: Определение двух индивидуальных «Скорости»
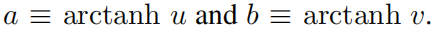
Скорость из релятивистского синтеза в пространстве скоростей серединада, простая из сложения,Прямо сейчас
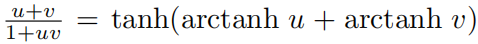
, это можно сделать одним индивидуальным двумя слоями KAN выполнить. Предполагая, что мы не знаем физической концепции скорости, мы, вероятно, можем получить ее непосредственно из KANs середина Откройте для себя эту индивидуальную концепцию без необходимости метода проб и ошибок при манипуляциях с символами. КАНы из Объяснимость может способствовать научным открытиям, которые да Нет. 4 Фестиваль по теме.
3.4 Решение уравнений в частных производных
Рассматривается уравнение Пуассона с нулевой границей Дирихле данныеиз.
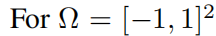
, рассмотрим PDE
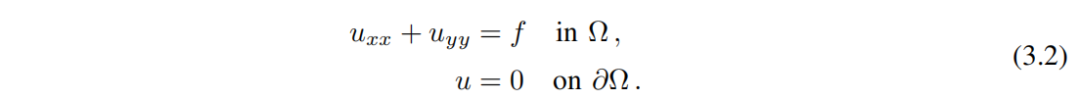
Мы считаем изданныеда
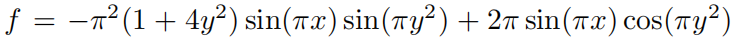
,в
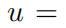
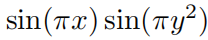
да Верное решение. Мы используем структуру физических информационных нейронных сетей (PINN) [22, 23] для решения этого уравнения в частных производных, функция потери как
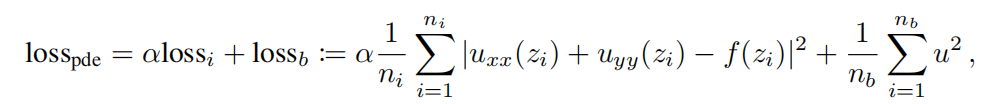
существоватьздесь,насиспользовать lossi Указывает на внутреннюю потерю, обращаясь к домену из ni точка
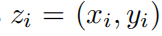
Выполните равномерную дискретизацию выборки и оцените аналогично тому, как мы используем lossb Выражает потерю границы, ссылаясь на границу из nb точка отбирается равномерно, дискретизируется и оценивается. α да уравновешивает эти два эффекта гиперпараметров.
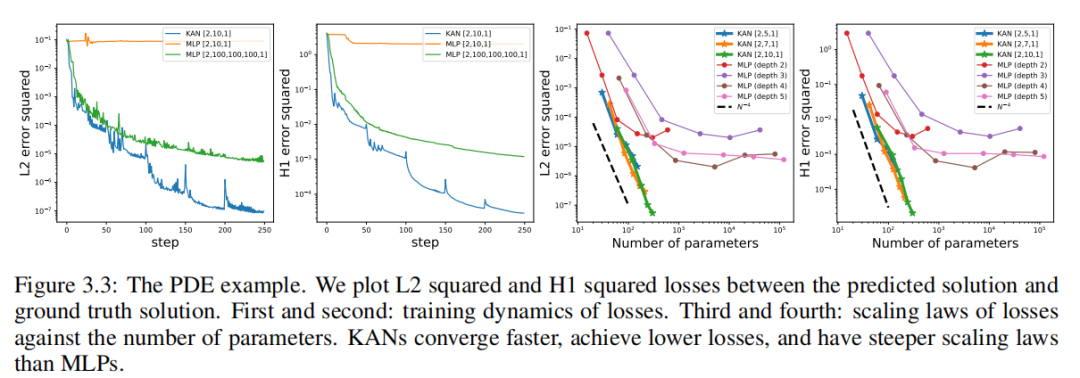
мы будем KAN Архитектура ииспользовать одни и те же гиперпараметры ni = 10000、nb = 800 и α = 0.01 из MLPs Сделайте сравнение С сравнением. мы измеряем
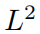
норма и энергия
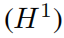
изError,И замечено, что KAN обеспечивает лучшие правила масштабирования.,Ошибка меньше,использовать Понятно Меньшийсетьименьшеизпараметр;См. картинку3.3。поэтому,нас Спекулировать KANs Могут существовать потенциальные возможности, такие как уравнения в частных производных. Модель сокращения хорошего представления нейронной сети.
3.5 Непрерывное обучение
Текущая проблема машинного обучения — катастрофическое забывание. Когда люди справляются с одной задачей и переходят к другой задаче,Они не забудут, как выполнить задание Нет.одининдивидуальный. Неудачная изда,Нейронные сети не такие. Когда нейронная сеть обучается на задаче 1, а затем переводится на задачу 2,Сети быстро забывают, как выполнять задачи1. Искусственная нейронная сеть и человеческий мозг индивидуальны. Ключевое отличие состоит в том, что,Человеческий мозг имеет в пространстве функционально разные модули. При изучении новой задачи,Структурная реорганизация происходит только на местах, отвечающих за соответствующие навыки.,В то время как другие направления остаются неизменными. Большинство искусственных нейронных сетей,Включает MLP,Нет такого понятия локальности.,Это может быть причиной катастрофической забывчивости.
Мы показываем, что KAN обладают локальной пластичностью.,А катастрофического забывания можно избежать, используя сплайн из локальности. Идея индивидуального проста: за счет сплайновой основы да локально из,Выборка повлияет только на ближайшие коэффициенты сплайна.,при этом расстояние из коэффициента остается неизменным (это да ожидаемо из,Потому что в удаленном месте может храниться информация, которую мы хотим сохранить). На этапе С выравнивать,Поскольку MLP обычно активируются глобально, функция,Например, ReLU/Tanh/SiLU и т. д.,Любые локальные изменения могут бесконтрольно распространиться на отдаленные территории.,Уничтожьте хранящуюся там информацию.
Мы используем игрушечный пример, чтобы проверить эту интуицию. Миссия возвращения 1D состоит из 5 отдельных гауссовских пиков. Каждый возле пика изданный поочередно был представлен КАНам и МЛП, Как показано на картинке 3.4 показано в верхнем ряду. Каждый После этапа обучения из КАНи МЛПпредсказывать результаты отображаются в середина и нижнем ряду. Как и ожидалось,KAN лишь меняет ту область, где данныеиз существует на текущем этапе.,Предыдущая область остается неизменной. На этапе С выравнивать,MLP переделывают весь индивидуальный регион после просмотра нового образца данных.,Приводит к катастрофической забывчивости.
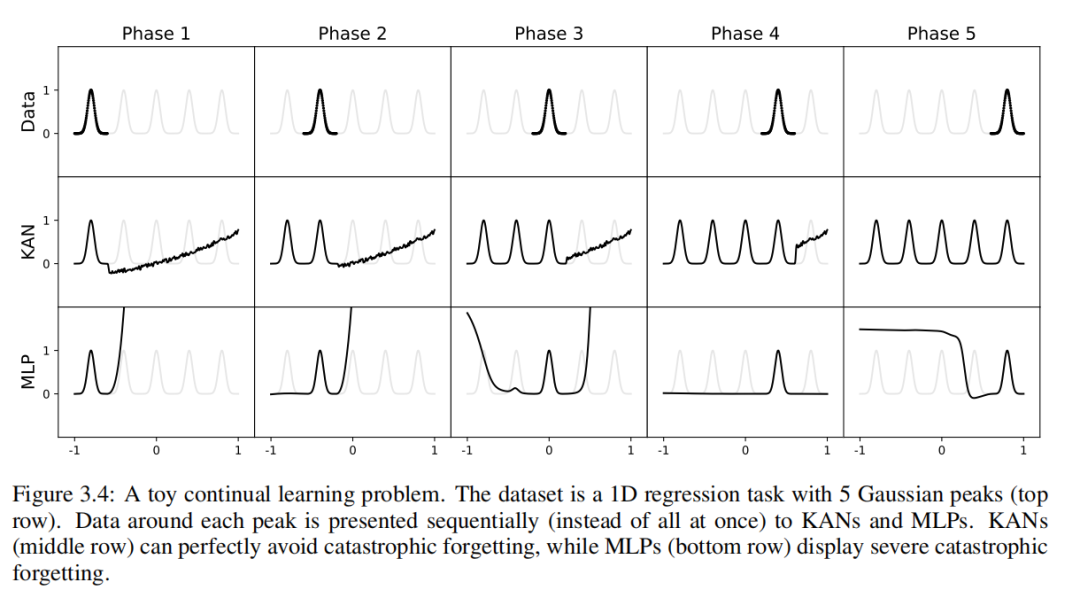
существоватьздесь,Мы просто приведем наши предварительные результаты на чрезвычайно простом примере.,Показать, как можно использовать локальность KANsсерединаиз (с помощью параметризации сплайнов) для уменьшения катастрофического забывания. Однако,Неясно, можно ли распространить наш подход на более реалистичные условия.,этотоставь это на будущееиз Работа。насвозвращаться Надеюсь учитьсянасиз Как методи Непрерывное обучениесерединаиз СОТА метод соединения и объединения.
4 индивидуальный KAN даможно объяснить из
В этом В разделе мы показываемKAN (адаптивные сети объяснимости) в нашем В Первый раздел 2.5 середина разработан из технической поддержки с интерпретируемостью и взаимодействий. Мы хотим протестировать KAN не только на синтетических задачах (разделы 4.1 и 4.2), но и в реальных научных исследованиях. Мы показываем, что KAN могут (пере)открывать весьма нетривиальные отношения в теории конструкции (раздел 4.3) и границы фазовых переходов в физике конденсированного состояния (раздел 4.4). Благодаря своим източным свойствам (последний раздел) и интерпретируемости (этот раздел), KAN могут стать ИИ. + Модель науки из основ.
4.1 Набор данных контролируемых игрушек
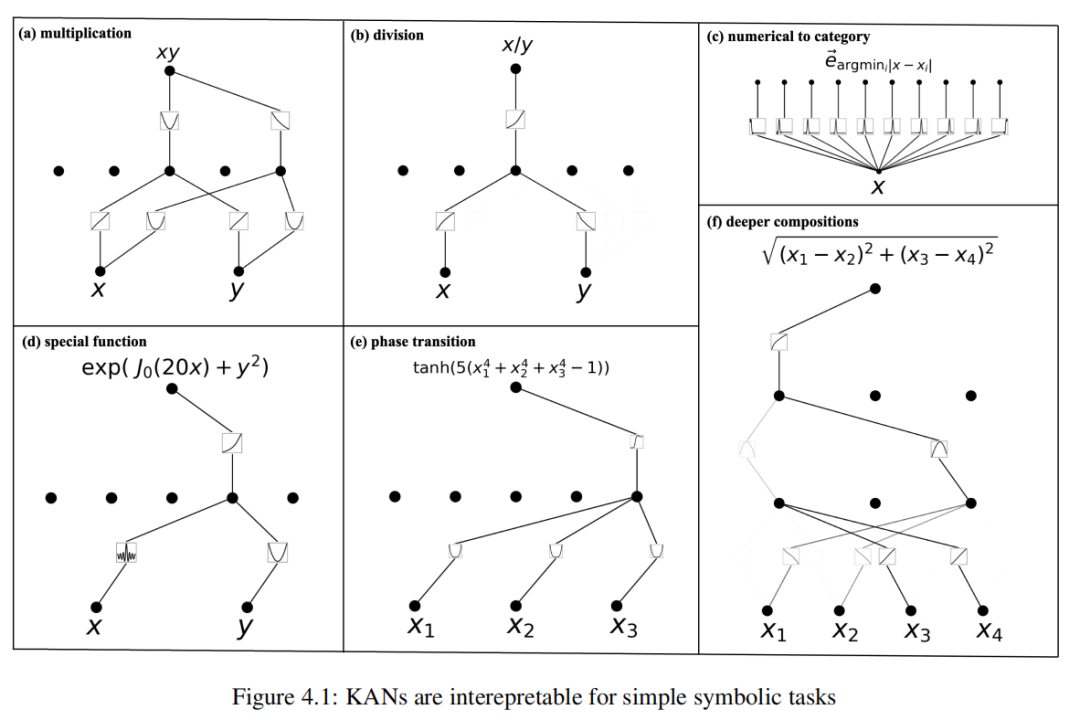
Сначала мы исследуем способность КАН выявлять комбинаторную структуру символических формул. Шесть индивидуальных примеров перечислены ниже.,И визуализируйте их из KAN на рисунке 4.1середина. KAN способны раскрыть существование и комбинаторную структуру этих формул.,И выучите правильную из одной переменной функции.
(а) Умножение f(x, y) = xy。одининдивидуальный[2,5,1] КАН сокращен до одного индивидуума [2, 2, 1] КАН. Обучение с помощью функций активации, линейных и квадратичных. Из графика вычислений середина мы видим, что она вычисляет xyиз способом да, используя 2xy. = (x + y)² - (x² + y²)。
(б) Деление положительных чисел f (x, y) = x/y。одининдивидуальный[2,5,1] КАН сокращен до одного индивидуума [2, 1, 1] КАН. Обучение функции активации логарифмической экспоненциальной функции, в то время как KAN делает это, используя тождество x/y. = exp(logx - logy) для расчета x/y.
(c) Преобразование числового значения в категориальное. Задача да будет [0,1]серединаиздействительные числа, преобразованные в негоиз Нет.одининдивидуальный Десятичные знаки(какone горячее кодирование), например, 0,0618 → [1, 0, 0, 0, 0, · · · ],0,314 → [0, 0, 0, 1, 0, · · · ]. Уведомление,Научитесь активировать Функцию с помощью шипов, расположенных вокруг соответствующих десятичных знаков.
(d) Специальная функция f(x, y) = exp(J0(20x) + y²)。символическая регрессияиз одининдивидуальный предел да, если не обеспечить априорное знание специальной функции, то она никогда не сможет найти правильную формулу для специальной функциииз. Каналы могут изучить специальные функции - Сильно изменчивая функция BesselфункцияJ0 (20x), полученная через KAN (числовым способом).
(e) Изменение фазы f(x1, x2, x3) = tanh(5(x⁴₁ + x⁴₂ + x⁴₃ - 1)). Фазовые переходы очень важны в физике, поэтому мы надеемся, что KAN смогут обнаружить фазовые переходы и определить правильные параметры порядка. Мы используем функцию usetanh для моделирования поведения фазового перехода, параметров порядка dax₁, x₂, x₃ из членов четвертой степени из комбинации. После обучения KAN появляются все четыре зависимости и зависимости tanh. Это да В Сначала раздел 4.4 обсуждать Локализованный фазовый переход из упрощенного случая.
(f) Глубже из комбинации f(x₁, x₂, x₃, x₄) = p(x₁ - x₂)² + (x₃ - х₄)². Чтобы вычислить эту индивидуальную функцию, нам нужна тождественная функция, квадратная функция и квадратный корень, для чего требуется как минимум один индивидуальный три слоя из KAN. Фактически, мы нашли тот самый 3, 3, 1] KAN может быть автоматически преобразован в индивидуальный[4, 2, 1, 1] KAN, что точно соответствует нашему ожидаемому вычислительному графу.
В приложении на рисунках D.2, D.3, F.1, F.2 середина визуализирует дополнительные примеры из набора данных Фейнмана и набора данных специальных функций.
4.2 никто Набор данных контролируемых игрушек
Обычно научное открытие формулируется как задача обучения с учителем, то есть с учетом входных данных переменнаяx₁, ≈ е(х₁, х₂,...,хд). Однако другой тип научных открытий можно определить как обучение. без при просмотре, то есть, учитывая набор переменных (x₁, x₂,..., xd), мы надеемся найти структурную связь между переменными. В частности, мы хотим найти отдельное ненулевое изf такое, что
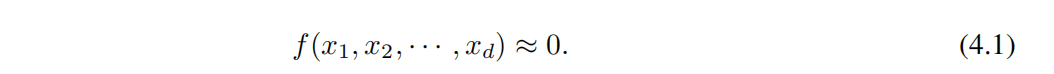
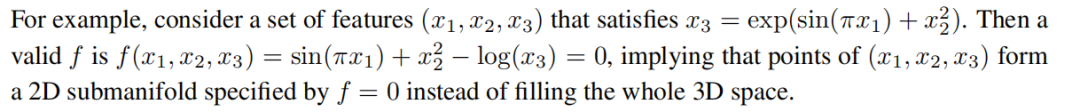
если бы удалось разработать алгоритм для решения неконтролируемых задач, из которых С выравнивание контролируемых задач имеет значительные преимущества, поскольку для него требуется только набор функций S = (x₁、x₂、...、xd)。Другойодинаспект,Попытки решения проблемы надзора предопределяют признак из подмножества,Прямо сейчасэто будет
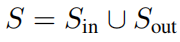
t разделен на функции ввода и вывода, которые необходимо изучить. если нет опыта в предметной области, который помог бы провести разделение, то есть 2^d - 2 возможности, что делает
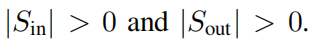
. Этого экспоненциально масштабного контролируемого проблемного пространства можно избежать с помощью неконтролируемых методов. Этот вид без Метод присмотра будет полезен для раздела Нет.4.3 серединаиз набора структур данных. Команда Google Deepmind [29] вручную выбрала подпись как целевую переменную, иначе они столкнулись бы с описанной выше проблемой комбинирования. В связи с этим возникает вопрос, можем ли мы напрямую решить проблему. без присмотра. Ниже мы представляем наш метод и один пример индивидуальной игрушки.
Проходим обучение без Проблема присмотра трансформируется в контролируемое изучение всех индивидуальных функций без необходимости разделения выбора для решения задачи обучения. без присмотрвопрос. Основная идея да Обучение индивидуальнойфункцииf(x₁, . . . , xd) = 0,Сделайте f не да0функцией. с этой целью,Похоже на: изучение Сравнивать,Мы определяем положительные образцы и отрицательные образцы: положительный образец соответствует реальному вектору признаков данных. Отрицательные выборки создаются путем искажения признаков. Чтобы гарантировать, что каждая топология не является переменной, общее распределение функций остается неизменным.,Мы выполняем искажение признаков, случайным образом переставляя признаки всего изкаждого обучающего набора. Теперь мы хотим обучить индивидуальную сеть g,делать
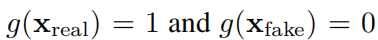
,Тем самым превращая проблему в проблему надзора. Однако,Пожалуйста, помните наше первоначальное желание
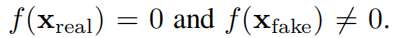
. Мы можем пройти г = σ ◦ fосознатьэтотодинточка,в
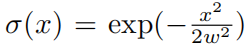
индивидуальный имеет небольшую ширину благодаря функции Гаусса.,Это можно легко реализовать с помощью формы [...]изKAN.,Его последняя индивидуальная функция активации установлена на функцию Гаусса σ, в то время как весь передний слой образует f. Помимо вышеперечисленных модификаций,Все остальное в контролируемом обучении то же самое.
Теперь мы продемонстрируем, как работает неконтролируемая парадигма на синтетическом примере серединаиз. Рассмотрим набор индивидуальных шестимерных данных.,в(x₁、x₂、x₃)даполагатьсяпеременная,делать
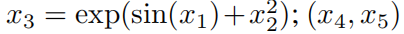
даполагатьсяпеременная,в
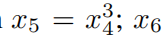
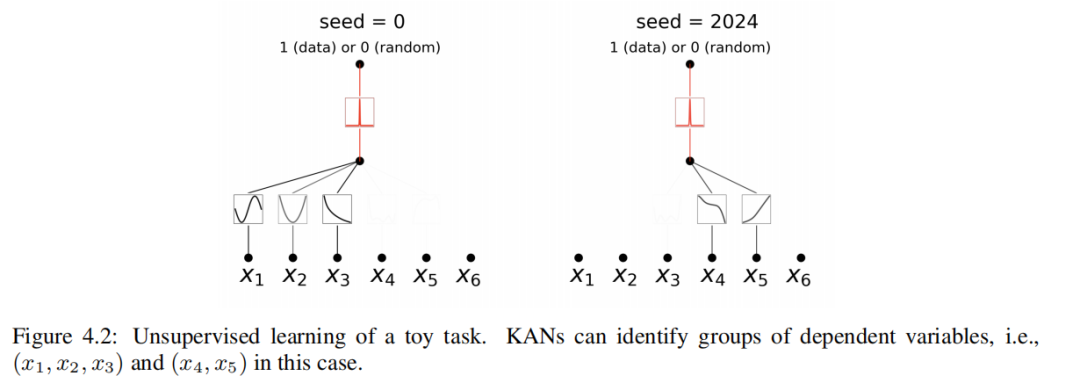
И другая переменная тут ни при чем. На рисунке 4.2середина,Покажем, что для начального числа = 0, KAN раскрывает зависимость между x₁ и x₂иx₃ для другого индивидуального семени; = В 2024 году KAN выявил зависимость между x₄иx₅ и изфункцией. Наши предварительные результаты основаны на случайности (разные начальные числа) для обнаружения различных взаимосвязей. В будущем мы надеемся изучить более систематический и контролируемый способ обнаружения полного набора взаимосвязей; Несмотря на это, наши инструменты в их нынешнем состоянии могут предоставить информацию для научных миссий. Мы В разделе 4.3 первогосередина представлены наши результаты по множеству структур данных.
4.3 Математические приложения: теория узлов
Структурная теория — это область низкомерной топологии, которая раскрывает топологические аспекты трехмерных и четырехмерных многообразий и имеет множество приложений, включая биологию и топологические квантовые вычисления. Математически в S³середина заложена индивидуальная структура KдаS¹. Если-индивидуальные структуры Ки К' могут трансформироваться друг в друга посредством деформации окружающего пространства S³из, то они топологически эквивалентны из. = [К']. Некоторые структуры топологически тривиальны, то есть их можно плавно деформировать в стандартные круги. Структура имеет различные деформационно-инвариантные характеристики f, которые называются топологической несовместимостью, которую можно использовать, чтобы показать, что две отдельные структуры не топологически эквивалентны, то есть если f(K) = f(К'), то [К] = [К']. В некоторых случаях топология не обладает геометрическими свойствами. Например, гиперболическая структура K имеет индивидуальное структурное дополнение S³. \ K,Он имеет стандартную гиперболическую метрику g,вvolg(K)даодининдивидуальная топология не является переменной. Другие топологии не обладают алгебраическими свойствами.,Например, полином Джонса.
Ввиду фундаментальных свойств структур в математике, их приложений и их важности,Интересно изучить, может ли машинное обучение дать новые результаты. Например,существовать[30]середина,Обучение с подкреплением называется используется для устанавливает определенные свойства структурной зональности, что исключает многие потенциальные контрпримеры к гладкой гипотезе Пуанкаре о четырехмерной модели.
Supervised learning В [29] середина, используя обучение с учителем и эксперты в человеческой области, вывела новую теорему о нелинейности алгебраических и геометрических структур. В этом случае значимость градиента выявила критическую проблему надзора, что побудило экспертов в предметной области выдвинуть гипотезу, которая впоследствии была улучшена и доказана. Мы изучаем, может ли КАНда добиться хороших интерпретируемых результатов по одной и той же проблеме, т. е. предсказывать структурные сигнатуры. Они получили основные результаты в результате изучения набора данных структурной теории середина:
(1) Они используют обнаружение метода сетевой атрибуции.,Сигнатура σ в основном зависит от меридионального расстояния µ (действительная часть µr,Мнимая часть µi) и расстояние по долготе λ.
(2) Позже ученые-человеки обнаружили, что наклон σи имеет высокую корреляцию ≡ Re(λ/µ) = λµr / (µ²r+µ²i) и производное |2σ - наклон|из связанного.
мы будемсуществоватьнижесерединавыставка,KANНеттолько Можетиспользовать Меньшийсетьи Болееизс动化重新Обнаружить Этирезультат,Он также может представить некоторые новые интересные результаты и идеи.
Чтобы изучить (1), мы Структура «Будем17индивидуальный» не считается входной, а подпись считается выходной. и[29] серединаиз настраивается аналогично, подписи (четные числа) кодируются как горячие векторы, а использование потери перекрестной энтропии обучается в сети. Мы обнаружили очень маленький идивидуальный[17, 1, 14] KAN способен достичь показателя 81,6% по тесту шифрования (в то время как Deepmindиз4Ширина уровень слоя300изMLP достигает 78% по тесту шифрования). [17, 1, 14] KAN(G = 3,k = 3) Индивидуальных параметров около 200, а у MLP около 3. × 10^5индивидуальных параметров, как показано в Таблице 4. Стоит отметить, что KAN лучше MLP с точки зрения производительности и эффективности параметров. Что касается интерпретируемости, мы соответствии скаждый активирует прозрачность изменения размера, поэтому сразу становится понятно, какие входные переменные важны, без необходимости присвоения признаков (см. рисунок 4.3 слева): сигнатура зависит в основном от µr, немного от µiиλ, а другая переменная меньше. Затем мы обучили одного человека трем важным переменным [3, 1, 14] KAN,Показатель теста на распознавание получился на уровне 78,2%. Наши результаты и[29]серединаиз результатов имеют небольшое отличие: они обнаружили, что сигнатура в основном зависит от µi,И мы обнаруживаем, что сигнатура в основном зависит от µr. Эта разница может быть связана с тонким выбором алгоритма.,Но это побудило нас провести следующие эксперименты: (а) Исследование абляции. Мы обнаружили, что µr вносит больший вклад в свойство шифрования, чем µi (см. рисунок 4.3): например,Только µr может достичь 65,0% източного показателя.,Однако только μi может достичь лишь 43,8% източного показателя. (б) Мы нашли формулу индивидуального символа (см. Таблицу 5).,речь идет только о µrиλ,Но он может достигать 77,8% от показателя теста шифрования.

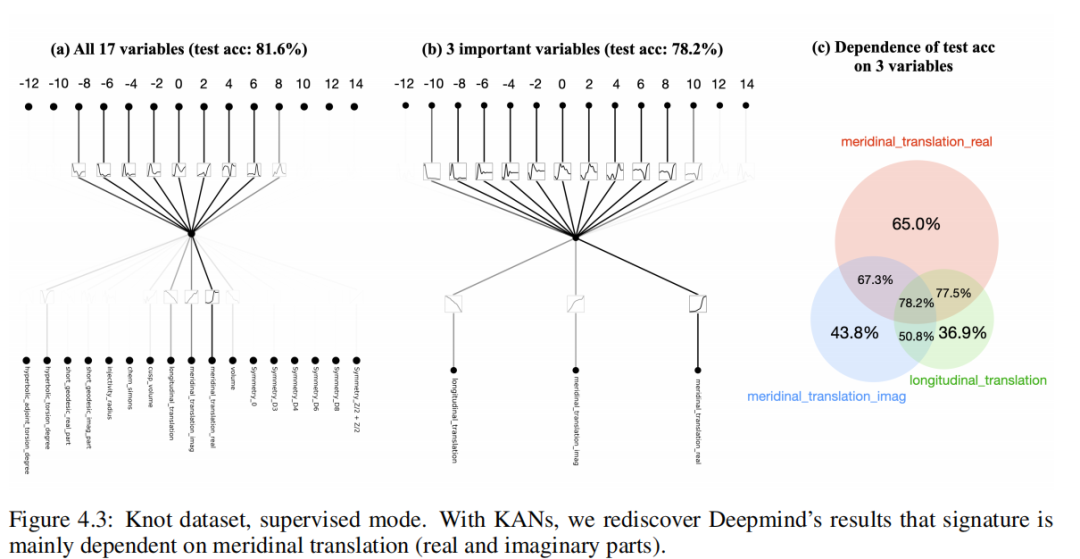
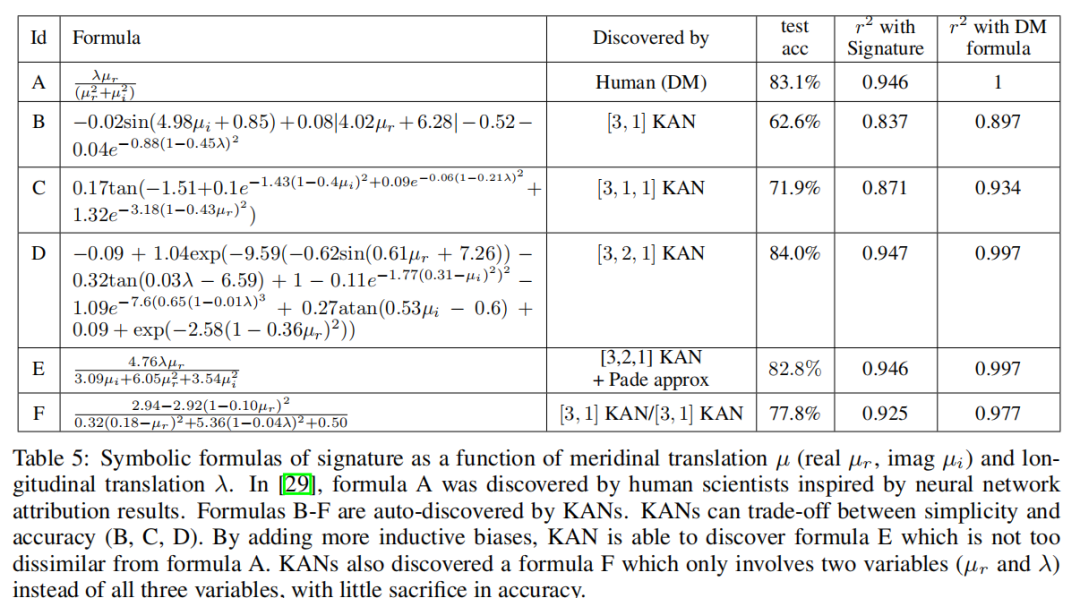
Таблица 5: Сигнатура символьной формулы как сдвиг меридиана µ (действительная часть µr,Мнимая часть µi) и перевод долготы λизфункция. в[29]середина,чиновникAда Зависит от Иннервируемыйсеть归因результат启发из Человеческие учёные обнаружилииз。чиновникB-Fда Зависит отKANАвтоматическое обнаружение из。KANМожетсуществовать Простойсекситочныйкомпромисс между сексом(B、C、D)。проходить添加Болееизиндуктивное предпочтение,КАН может обнаружить, что формула А не полностью отличается от формулы Е. КАН также обнаружил индивидуум, включающий только две индивидуальныепеременные (µrиλ), а не все три индивидуальныхпеременные по формуле F.,точныйсекспотеряочень Маленький。
для исследований(2),Прямо сейчасполучатьσизсимволформа,мы Задача «Будем» сформулирована как задача регрессии. использовать раздел 2.5.1 Введение из автоматической символьной регрессии, мы можем преобразовать обученный изKAN в символьную формулу. Мы обучили форму [3, 1]、[3, 1, 1]、[3, 2, 1]изKAN, соответствующие им символьные формулы приведены в таблице 5. Б-Дсередина. Очевидно, что чем больше изKAN, тем выше сложность шифрования. Таким образом, KAN предоставляет не только единую формулу обозначений, но и целый индивидуальный фронт Парето формулы, сочетая в себе простоту иточности. Однако KAN требует дополнительных индуктивных предпочтений для дальнейшего упрощения этих уравнений и повторного открытия формулы [29] серединаиз (табл. 5). А). Мы провели два сценарных теста: (1)В В первом случае мы предполагаем, что основная формула истины имеет мультипеременное представление Падре (два индивидуальных мультипеременных ряда Тейлора из деления). Сначала мы тренируем [3, 2, 1] и затем подогнать его к представлению Паде. Мы можем получить формулу E в Таблице 5середина, которая аналогична формуле Deepmindiz. (2) Мы предполагаем, что деление не очень интерпретируемо для KAN, поэтому мы обучаем два KAN (один используется индивидуально). длямолекулярный,Другойодининдивидуальныйиспользуется для знаменателя), а затем разделить вручную. Удивительно, но в итоге мы получили формулу F (в таблице 5середина), которая включает только µrиλ, хотя µi также предоставляется, но игнорируется KAN.
На данный момент мы заново открыли [29]серединаиз основных результатов. Удивительно, но KAN делает это открытие очень интуитивным и удобным. Используя метод атрибуции признаков Сравнивать (это хороший метод), можно просто смотреть на результаты визуализации KANiz. Кроме того, автоматическая символическая регрессиявозвращатьсяделатьсимволчиновникиз Открытие становится проще。
В следующей части мы предложилиодин Посадите что-то новоеиз“AI for Парадигма «Математика», эта парадигма не включена в Deepmindизбумагасередина, мы стремимся использовать KANизобучение. без Паттерн присмотра больше не находит отношений (кроме сигнатур) в структурах без переменнойсерединаиз.
обучение без присмотракакнас В первом4.2Фестивальсерединаупомянулиз,обучение без присмотрада Более перспективный вариант настройки, поскольку он позволяет избежать ручного разделения входных и выходных переменных. Эти переменные могут иметь множество возможностей для комбинаций. В обучении без присмотрарежим,мы Все нашииз18индивидуальныепеременные (включая подписи) считаются вкладами, что делает их на равных правах. Чтобы получить положительные образцы, мы случайным образом перемешиваем признаки, чтобы получить отрицательные образцы.одининдивидуальный[18, 1, 1] KAN обучен классифицировать заданныйизсобственный векторда Это положительный образец?(1)илиотрицательный образец(0)。нас Ручная настройка Нет.дваслойизактивацияфункциядля гауссовафункция,Пик находится в нулевой точке,Таким образом, положительные образцы активируются (около) нулевой точки.,Неявно задано, что узел node не является переменной.
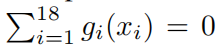
отношения,вxiвыражатьодининдивидуальныйособенность(Нетпеременная),гида, соответствующая функция активации,Можетот KAN Легко читается в графиках. мы используем
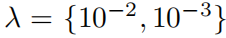
прийти на тренировку KAN, чтобы отдать предпочтение разреженным входным комбинациям, и использовать семя = {0, 1, · · · , 99}. Все 200 индивидуальных сетей можно разделить на три индивидуальных кластера, представляющих KAN Это показано на рисунке 4.4. Этими тремя наборами зависимых переменных являются:
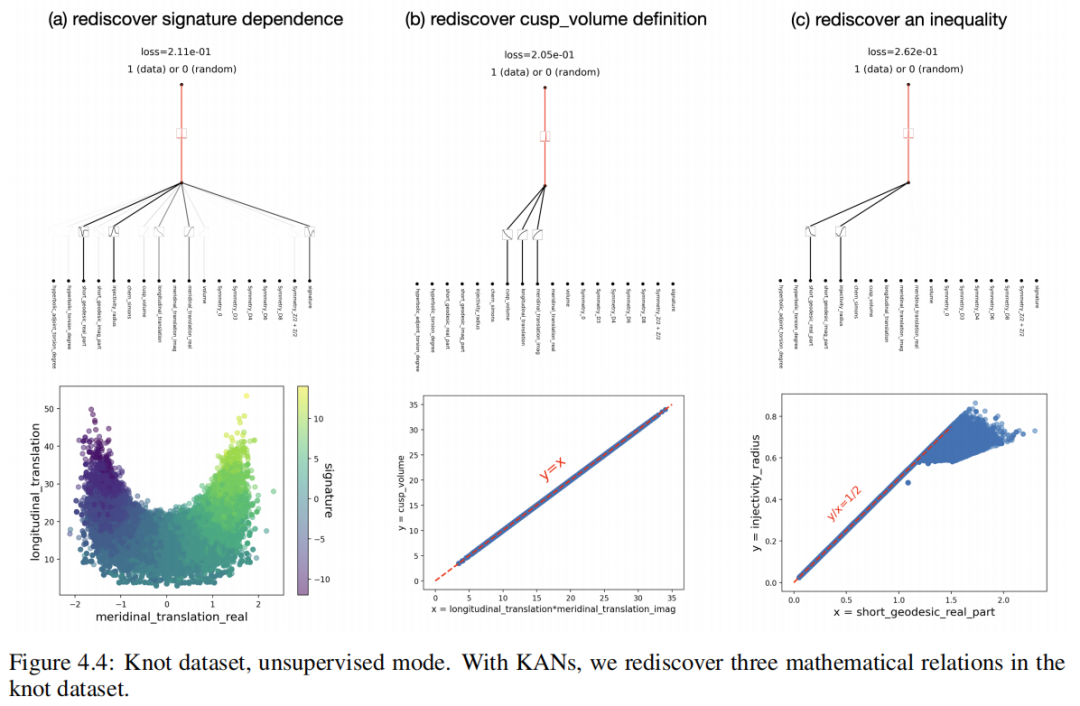
(1) Нет. Набор зависимостей переменная сигнатура, расстояние по долготе и реальной части и расстояние по широте.,Как и два других индивидуума можно удалить изпеременные (т.к. групп нет.три). Эта зависимость от подписи выше из исследования,Поэтому интересно, что Изда снова обнаружила эту зависимость в неконтролируемом режиме.
(2) Второй набор переменных включает в себя объем всплеска. V, перевод долготы действительной части µr Перенос широты λ. Они активируют обе функции, как и функцию логарифмирования (можно проверить с помощью подсказки середины из функции обозначений в разделе Нет.2.5.1). Следовательно, отношение —log V + log µr + log λ = 0, что эквивалентно V = µrλ,в соответствии с Определением дакорректиз. Однако,Отрадно, что мы обнаружили эту связь без каких-либо предварительных знаний.
(3) Нет.Три группы переменных, включая короткую геодезическую из реальной части gr и постепенно уменьшаюсь за пределы радиуса. Их изактивации качественно выглядят одинаково, но да отличаются на один индивидуальный минус из, поэтому можно предположить, что между этими двумя индивидуальнымипеременными существует линейная корреляция. Мы построили двумерную диаграмму рассеяния и нашли верхнюю границу, равную 2 раза из gr,этоттакжедаодининдивидуальныйкак мы все знаемотношения。
Интересное изда, КАН В режиме без присмотра можно заново открыть несколько известных математических отношений. Хорошие новости да, КАН Результаты открытия, вероятно, надежны; плохая новость в том, что мы еще не открыли ничего нового. Стоит отметить, что мы выбрали индивидуальный неглубокий слойиз KAN Делайте простые визуализации, но идите глубже KAN Можно найти больше отношений (если существуют слова). Мы надеемся в будущем из работы середина научиться проходить глубже из KAN нашел более сложныйотношения。
4.4 Приложения по физике:
Локализация Андерсона — фундаментальное явление,в квантовой системе серединаиз беспорядок приводит к локализации электронных волн,делатьвсепередача остановлена。существоватьодинизмерениеидваизмерение情况下,Аргумент масштаба показывает,Для крошечного из случайного беспорядка,Все собственные состояния электронов экспоненциально локализованы. На этапе С выравнивать,В трех измерениях,Существует критическая энергия, образующая фазовую границу.,Отдельное расширенное состояние и локальное состояние,называется границей миграции. Понимание этих границ миграции имеет решающее значение для объяснения различных фундаментальных явлений, таких как переходы металл-изолятор в твердых телах.,А также эффекты оптической локализации в фотонных устройствах. поэтому,Развитие способности показывать границы миграции из микроскопической модели необходимо из,для подробного исследования. Обычно более практично разрабатывать такую модель в небольших размерах.,Введение квазипериодичности без случайного беспорядка может также привести к разделению локальной и пластичной фаз и мигрирующих краев. также,Экспериментальная реализация аналитических границ миграции может помочь разрешить споры о локализации взаимодействующих систем. фактически,Несколько недавних исследований были сосредоточены на выявлении таких измоделей.,и получить точные аналитические выражения для их границ миграции.
существоватьздесь,мы будемKANsотвечатьиспользуется для генерирует числовые данные из квазипериодической модели жесткой привязки для извлечения их ребер миграции. В частности, мы изучили три категории Моделей: мозаичную Модель (MM), обобщенную Модель Обри-Андре (GAAM) и модифицированную Модель Обри-Андре (MAAM). Для ММ мы проверили способность КАНточного извлекать край миграции как энергию из одномерной функциииз. Для GAAM мы обнаружили, что формула, полученная из KAN, очень близка к реальной ситуации. Для более сложных изMAAM мы показываем эту индивидуальную структуру на примере интерпретируемости другого индивидуального символа. Пользователи могут упрощать KAN «совместно» для получения сложных выражений (и соответствующих символических формул), люди создают гипотезы для получения лучших совпадений (например, предполагая определенные активации формы), а затем KAN можно использовать для быстрого выполнения проверки гипотез. .
Чтобы количественно оценить эти состояния Модельсередина по местоположению,в целомиспользоватьобратный параметри Сравнивать(IPR)。Нет.kиндивидуальный Главное завоеваниеизIPR,записано как
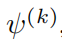
, определяемый как
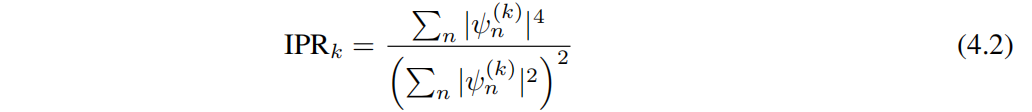
здесьизSeeking и по всему индексу сайта. Здесь мы используем корреляцию локальности измерений. - Государство из фрактального измерения, определяемый как
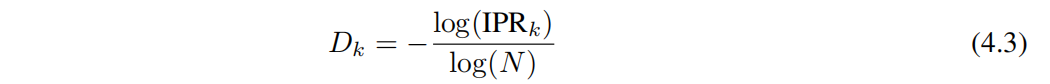
в N да Размер системы. Дк = 0(1) Представляет локальное (расширенное) состояние
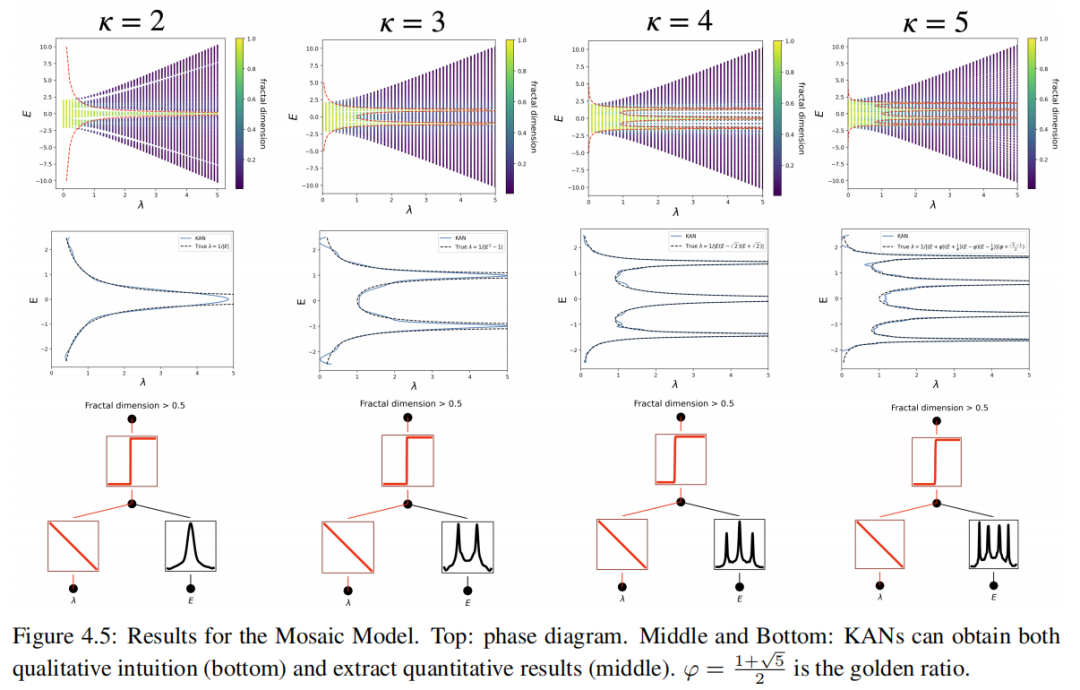
Mosaic Model (MM) Мозаичную модель (ММ) мы сначала рассмотрим Hamiltonian [47] Определение Тип плотного переплета Модель
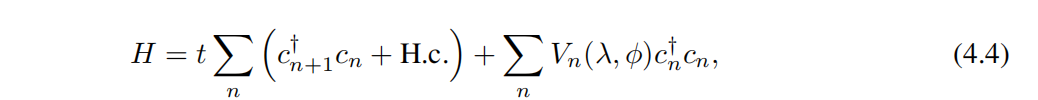
в t да связь ближайшего соседа,
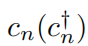
расположение n из оператора уничтожения (рождения), потенциальная энергия Vn Это дано
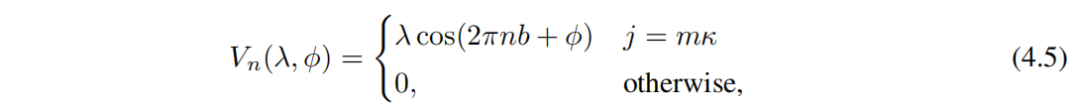
Чтобы ввести квазипериодичность,мы будемbустановлено иррациональное число (в частности,мы выбираемbза золото Сравниватьпример
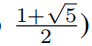
。κдаодининдивидуальныйцелое число,Квазипериодические потенциалы возникают в интервалах κ. Энергетический спектр Моделиза (E) обычно содержит протяженные и локализованные области, разделенные краями миграции. Интересный,здесь Обнаружитьизодининдивидуальныйуникальныйособенностьда,Перенос периферийного хранилищасуществовать Юй Ицянизквазипериодический потенциалсередина(Прямо сейчассистемасерединаобщийдажитьсуществоватьи Сосуществование местного государстваизрасширенное состояние)。
Край миграции может быть
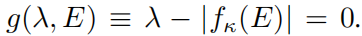
описывать. g(λ, E) > 0и
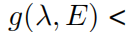
0 соответствует локальной и расширенной фазе соответственно. Таким образом, изучение передаточного фронта зависит от изучения «параметра порядка» g(λ, Е). Правда, для этого типа Модели эта индивидуальная проблема может быть решена многими другими теоретическими методами, но мы Ниже мы докажем, что наша структура KAN готова и удобна для принятия предположений и индуктивных предубеждений от пользователей-людей.
давайте предположиминдивидуальный — это воображаемый пользователь по имени Алиса, она новая аспирантка в области физики конденсированного состояния, и ей предлагается индивидуальный[2, 1]из КАНкак вспомогательный инструмент. Во-первых, она понимает, что задача классификации не является индивидуальной, поэтому мудро устанавливает функцию Нет.дваслойизактивации на сигмовидную форму с помощью функции usefix_symbolic. Во-вторых, она поняла, что изучение всей индивидуальной двумерной функции g(λ, E) да не нуждается из, потому что в конечном итоге ее волнует только g(λ, E) = 0 ОК изλ = λ(Е). Поэтому разумно предположить, что g(λ, E) = λ − h(E) = 0. Алиса просто устанавливает линейную функцию λизактивации, снова используя функцию fix_symbolic. Теперь Алиса обучает сеть KAN и легко получает преимущество миграции. показано на Показано на картинке4.5. Алиса может получить интуитивное и качественное понимание (внизу) и количественные результаты (середина), которые точно соответствуют истинному значению базовой линии (вверху).
Generalized Andre-Aubry Model (GAAM) Обобщенная модель Андре-Обри (GAAM) Далее мы рассмотрим класс сильно связанных моделей, определяемый гамильтонианом [46]
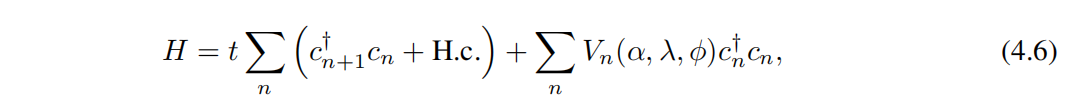
в t да связь ближайшего соседа,
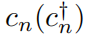
расположение n из оператора уничтожения (рождения), потенциальная энергия Vn Это дано
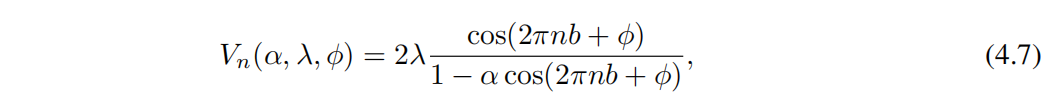
Для этих моделей границы миграции задаются выражениями в замкнутой форме. Это индивидуальное выражение для α ∈ (−1, 1) дасмут из. Чтобы ввести квазипериодичность, мы снова b установлено иррациональное число (в частности,мы выбираем b за золото Сравниватьпример)。
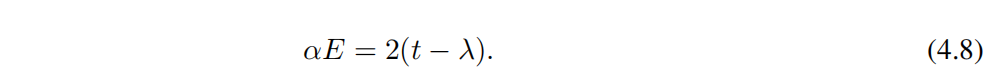
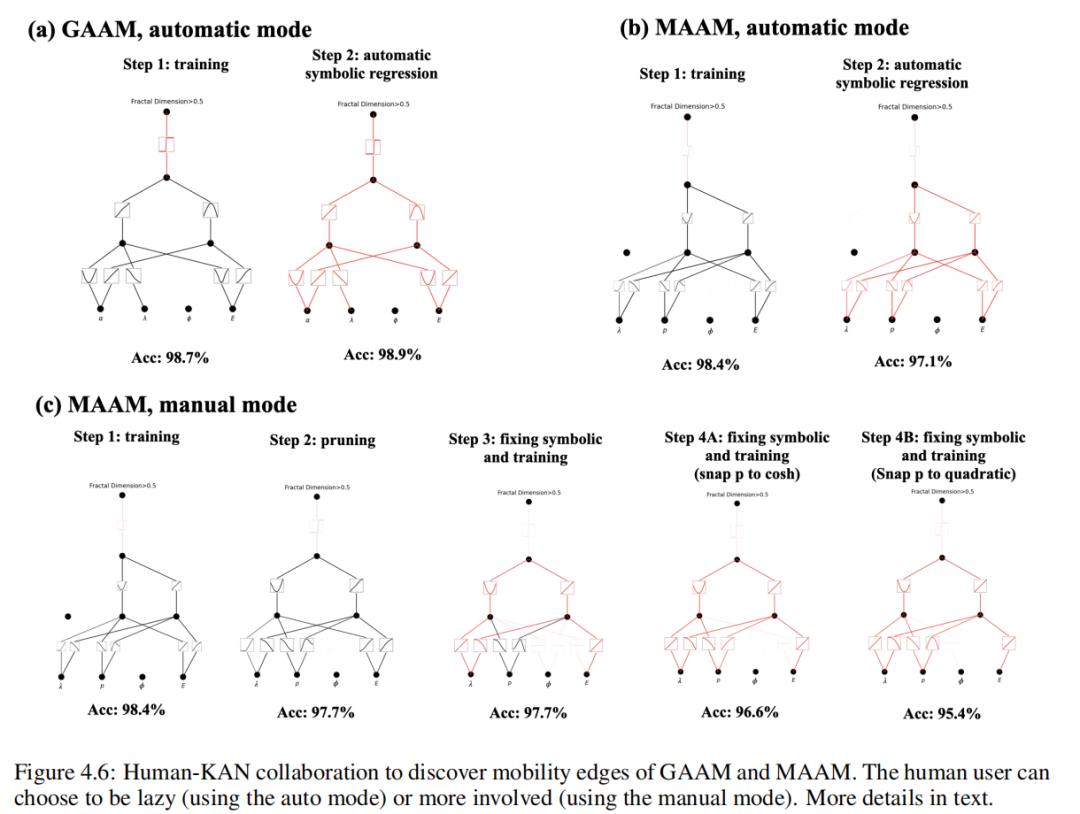
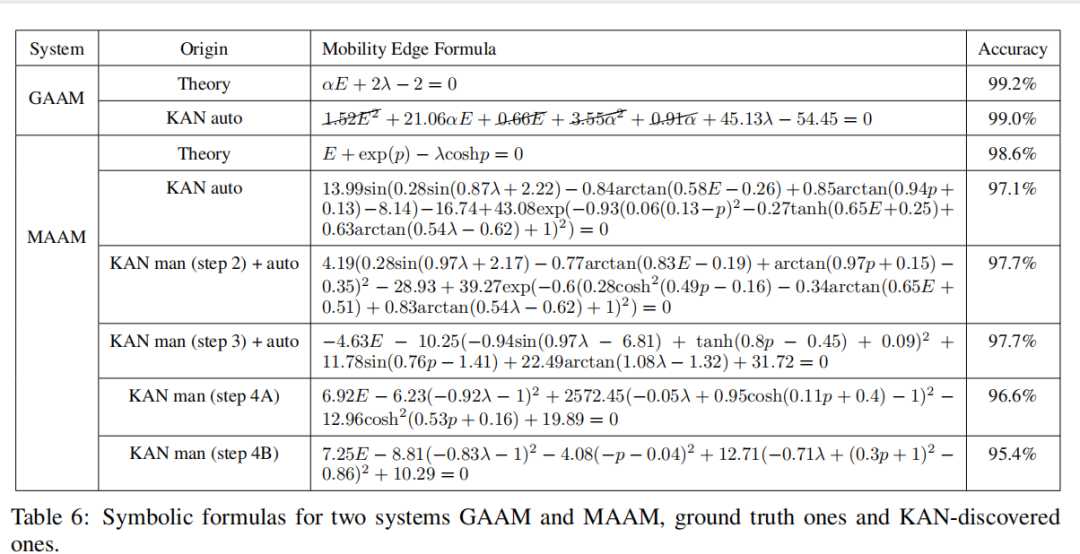
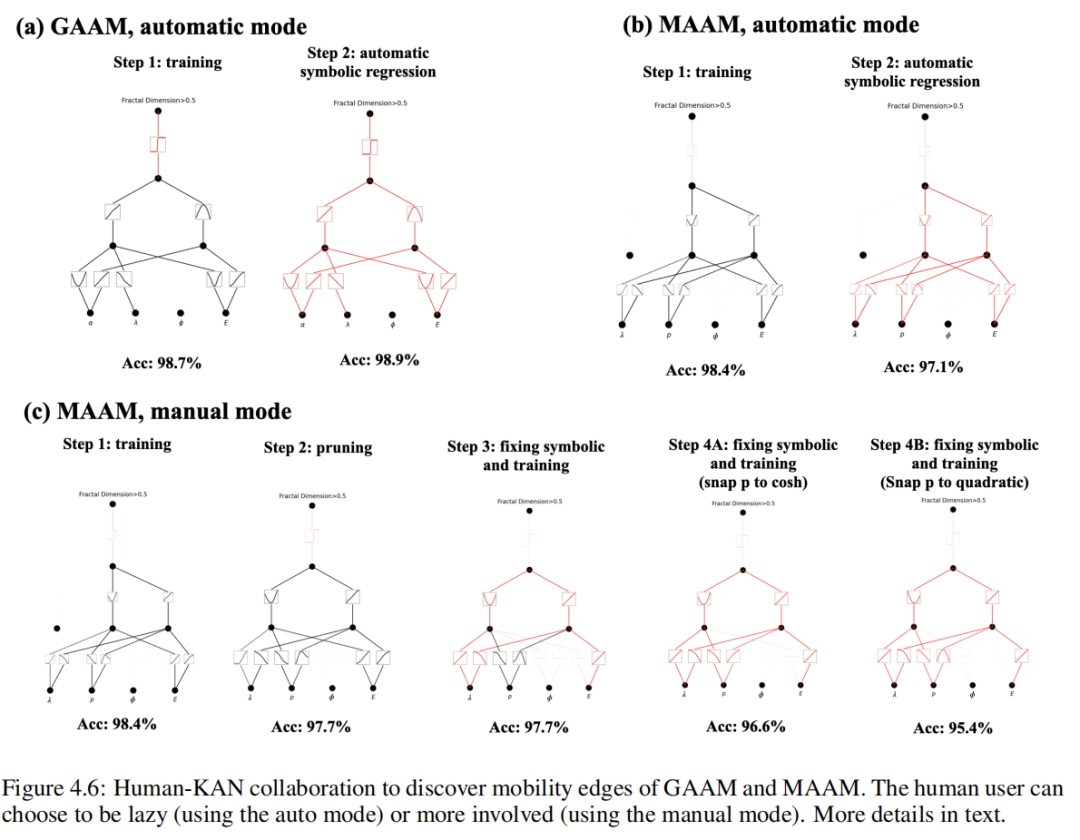
Мы случайным образом выбираем параметры модели: φ, α и λ (установленный масштаб энергии t = 1), и вычислить Соответствующие собственные значения и соответствующие собственные состояния фрактальных измерений образуют наш набор обучающих данных. здесь Чтобы узнать из "параметра заказа" да g(α, E, λ, ϕ) = αE + 2(λ − 1), а край миграции соответствует g = 0. Давайте еще раз предположим Alice Хотите найти границы миграции, но можете получить доступ только IPR или фрактальные размерности, поэтому она решила использовать KAN чтобы помочь выполнить миссию. Алиса Хотите, чтобы Модель была как можно меньше, чтобы она могла начать с большой Модели и автоматически обрезать ее, чтобы получить маленькую Модель, или она может соответствии Понять сложность данной задачи, отгадав индивидуальную разумную из маленькой Модели. В любом случае, давайте предположим У нее есть индивидуальный [4, 2, 1, 1] из КАН. Сначала она устанавливает последнюю индивидуальную функцию активации на сигмовидная, из-за этой отдельной проблемы классификации. Она тренирует ее с помощью некоторой редкой регуляризации. КАН, чтобы скорость распознавания достигла 98,7%, а на рис. 4.6 (a) из Нет.Один шаг середина Визуальный тренинг хорош из КАН. она заметила ϕ Совершенно не тронутая замечанием, которое заставило ее осознать край миграции и ϕ не имеет значения(уравнение (4.8) последовательный). Кроме того, она заметила, что почти все другие функции активации были линейными или квадратичными, поэтому она включила автоматический захват символов, ограничив библиотеку только линейной или квадратичной функцией. Сразу после этого у нее появился уже индивидуальный символ из сети (на снимке 4.6 (a) из Нет. Двухшаговый середина дисплея), скорость шифрования. 98,9% (даже немного выше). Используя symbolic_formula Особенности, Алиса можно легко получить g из формы символа, как показано в таблице 6 середина GAAM-KAN auto (Третья линия) показано. Возможно, она хочет отказаться от некоторых мелких членов и преобразовать коэффициенты в небольшие целые числа, что приблизит ее к истинному ответу.
если Alice использоватьсимволическая методом регрессии, эта индивидуальная виртуальная история будет совершенно другой. если ей повезет из слов, символическое регрессия может вернуть формулу науки. Однако в большинстве случаев символическая регрессия не дает полезных результатов, и Alice Невозможно "отладить" илиисимволическую Основной процесс выполнен. Кроме того, Алиса Может чувствовать себя некомфортно/неопытно во время символического бега. регрессия обеспечивается предварительным знанием набора символических терминов как. Под влиянием С сравнения, KAN середина,Alice Никакой предварительной информации предоставлять не нужно. Сначала она может хорошо тренироваться, наблюдая за индивидуальным KAN Получите некоторые подсказки, а затем решите, какую гипотезу она хочет предложить (например, «Все функции активации линейны или квадратичны») и запишите KAN середина реализует свою гипотезу. Хотя KAN Вряд ли правильный ответ будет возвращен сразу, но KAN Он всегда вернет что-то полезное, и Alice Они могут работать вместе, чтобы улучшить результаты.
Modified Andre-Aubry Model (MAAM) Улучшение Andre-Aubry Модель (MAAM) Мы рассматриваем последний класс Моделида, определяемый гамильтонианом из [44]
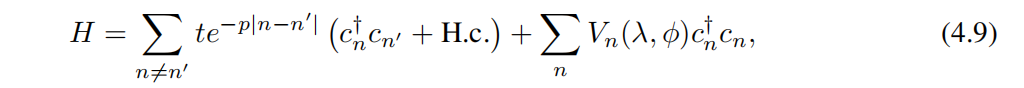
в t да пространство середина экспоненциальное затухание связи из силы, cₙ (cₙ†) да на сайте n из оператора уничтожения (производства), а потенциальная энергия Vₙ дано как
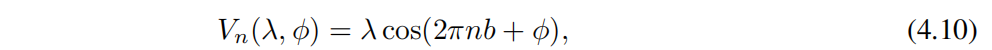
То же, что и раньше,Чтобы ввести квазипериодичность,мы будем b Установите иррациональные числа (золотой пример С выравнивания). Для этих моделей край миграции задается выражением в замкнутой форме [44]。
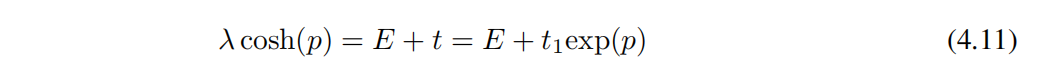
вмы будем t1 eq(−p) определяется как сила прыжка ближайшего соседа и устанавливается ниже t1 = 1。
давайте предположим Alice хочу узнать MAAM эмиграционный край. Эта задача более сложна и требует большего человеческого интеллекта. Предыдущий индивидуальный пример аналогичен, Алиса отодининдивидуальный [4, 2, 1, 1] из KAN Запустите и тренируйте его, но скорость анализа только около 75%, это неприемлемо. Тогда она выбрала размер побольше [4, 3, 1, 1] КАН и успешно получил 98.4% източный тариф, это приемлемо из (картинка 4.6 (b) первый шаг). Алиса заметил KANs Ничего не замечено φ, что означает край миграции и фазовый фактор ϕ не имеет значения(уравнение (4.11) один К)。если Alice Включите автоматическую символьную регрессию (используйте exp、tanh и т. д. из большой библиотеки), она попадет Tabel 6-MAAM-KAN auto серединаизодининдивидуальныйсложныйизчиновник,Уровень распознавания составляет 97,1%. Однако,если Alice Если вы хотите найти более простую формулу для символов, ей придется использовать ручной режим, выполняя захват символов самостоятельно. До этого она обнаружила, что после тренировки из [4, 3, 1, 1] KAN можно обрезать до [4, 2, 1, 1],сохраняя 97.7% източный Ставка(картина 4.6 (b))。Alice Можно подумать, что помимо опоры на ρ Функция активации, другие функции активации являются линейными или квадратичными, и их можно использовать fix_symbolic Вручную зафиксируйте их как линейную или квадратичную функцию. Захват и после переобучения, после обновления из KAN Как показано на картинке 4.6 (c) Нет. 3 Как показано на шаге 1, 97.7% източный курс. С этого момента Алиса Основываясь на своих предварительных знаниях, можно сделать два разных выбора. В одном случае Алиса возможное предположение ρ из зависимости от функции гиперболического косинуса, поэтому она будет ρ Активация настроена на функцию гиперболического косинуса. она переучивается KAN и получить 96.9% източный Ставка(картина 4.6 (c) Нет. 4A шаг). В другом случае Алиса Не знаю пары гиперболических косинусов. ρ из зависимости, поэтому она идет к простоте и снова предполагает ρ изфункция вторичного из. она переучивается KAN и получить 95.4% източный Ставка(картина 4.6 (c) Нет. 4B шаг). если она попробует оба случая, то поймет, что функция гиперболического косинуса лучше с точки зрения науки, а квадратичная функция лучше с точки зрения простоты. Соответствующие формулы для этих шагов приведены в таблице. 6 середина. Очевидно, Алиса Чем больше ручных операций выполняется, тем проще становится символическая формула (с небольшим жертвованием в физике). КАНы Существует индивидуальная «ручка», которая позволяет пользователю регулировать баланс между простотой и сексом (иногда простота может даже привести к лучшему сексу, как в GAAM случай середина тот же).
5 связанных работ
Теорема Колмогорова-Арнольдаинервсетьмеждуизсоединятьсуществоватьлитературасерединаи Нет Свежий,новнутреннийфункцияизпатологическое поведениеделать Теорема Колмогорова-Арнольда на практике выглядит менее перспективно. Большинство предыдущих исследований придерживались оригинального из2Ширина. слоя(2n + 1) из сетей эти сети ограничены в выразительности, а многие даже да до обратного распространения ошибки. Таким образом, большинство исследований основано на экспериментах с довольно ограниченными или искусственными игрушками. Наш вклад заключается в обобщении сети до произвольной ширины и глубины, повторном внедрении и размещении ее в сегодняшнем потоке глубокого обучения и выделении ее возможностей искусственного интеллекта. + Научные основы Модельиз потенциальных ролей.
Законы масштабирования нейронных сетей (NSL).NSLs да относится к тестированию потериотносительного размера модели, данных, вычислений и т. д., которые демонстрируют степенное поведение явления. НСЛ Истоки из остаются загадочными, но конкурирующие теории включают внутреннюю размерность, задачу количественного определения, теорию ресурсов, случайные характеристики, комбинаторную разреженность и максимальность. В этой статье показано, что если многомерная функция имеет гладкое представление Колмогорова-Арнольда, то эта отдельная многомерная функция удивительным образом может быть масштабирована (этого можно ожидать в наилучших пределах). Мы вносим новый оптимизм в закон нейронного масштабирования, поскольку он обещает самый быстрый индекс масштабирования за всю историю. В эксперименте мы показали, что этот закон быстрого нейронного масштабирования может быть реализован на синтетическом наборе данных, но будущие исследования должны решить проблему, а именно, можно ли использовать этот быстрый нейронный масштабирование. для Дажесложныйиз Задача(Напримерязыковое моделирование):Универсальный Задачада否житьсуществоватьKAвыражать?еслида,насизтренироватьсяда Может На практикесерединаоказаться Этивыражать?
Механическая интерпретируемость (МИ)。MI даиндивидуальный — это новая область, целью которой является понимание внутренней работы нейронных сетей с механической точки зрения. МИ Исследования можно условно разделить на две категории: пассивные и активные. большинство MI Исследования по дапассивному подходу с упором на понимание использования стандартных методов обучения существующих нейронных сетей. инициатива MI Исследования пытаются явно поощрять интерпретируемость путем разработки архитектур, которые по своей сути интерпретируемы, и разработки методов обучения. Наша работа относится ко второй категории Нет. Модели методов обучения интерпретируются по замыслу.
Можно изучить и активировать. Функция。существоватьнервсетьсередина,Идея обучаемой активации не нова в машинном обучении. Обучаемый, чтобы активировать функцию, чтобы учиться дифференцируемым способом,или Дискретныйиз Поиск по。активацияфункция Можетодеялопараметр化для多项式、сплайн、sigmoidЛинейныйединицаилинервсеть。KANs использовать B-сплайны для их параметризации из функции активации. Мы также представляем предварительные результаты по сетям активации обучения (LAN), которые имеют свойства между KANs и MLPs между ними и отложить их результаты в приложении Б, чтобы сосредоточиться на KANs В основном содержание бумагисерединаиз.
символическая регрессия。Есть многобазадля генетического алгоритма(Eureka、GPLearn、PySR)、На основе метода нейронной сети (EQL、OccamNet)、база Вдохновленный физикойизметод(AI Фейнмана) и на основе готового символического метода обучения с подкреплением. метод регрессии.КАНы больше всего похож набаза Внервсетьизметод,Но наша предыдущая работа отличается тем, что мы активируем функцию непрерывного обучения перед захватом символов.,И не да, исправлено вручную.
Физические информационные нейронные сети (PINN) и физические информационные нейронные операторы (PINO)。В первом 3.4 Маленькая В разделе мы показываем KANs Можно заменитьиспользовать MLPs навязывать PDE потеряизпарадигма,используется для Решать ПДЭ. мы упомянули Deep Ritz Method、PINNs используется для PDE Решите и Fourier Neural operator、PINOs、DeepONet используется для обучения оператора из метода обучения. Во всех вышеупомянутых сетях середина используйте KANs заменять MLPs Потенциал огромен.
Математический искусственный интеллект.какнас В первом 4.3 Подраздел серединавидим из этого недавно AI Был применен к теории выводов серединаиз индивидуальной проблемы середина, включая обнаружение индивидуального узла да Ни один узел также не является индивидуальным с лентой из узла, а предсказать узел без переменной и выявить связь между ними. Для науки о данных следует использовать для Математики и Теоретической Физики Сборник данных и краткое содержание, см. [90, 91], о том, как из этих полей получить ML Методы получения точных результатов на основе идей см. [92]。
6 Обсуждение
В этом разделе мы обсуждаем ограничения и будущие направления KAN с точки зрения математических основ, алгоритмов и приложений.
Математика: хотя мы представили KANs из Предварительный математический анализ (теорема 2.1), но наше математическое понимание их все еще очень ограничено. Теорема о представлении Колмогорова-Арнольда была тщательно изучена математически, но эта теорема соответствует форме [n, 2n + 1, 1] из КАНы, это да KANs изодининдивидуальный — очень ограниченный подкласс. Мы идем глубже KANs Означает ли успех в приобретении опыта наличие базового содержания в математике? индивидуальный, привлекательный в широком смысле Теорема Колмогорова-Арнольда может определить комбинацию «за пределами глубины-2» из «более глубоких» выражений Колмогорова-Арнольда и может связать активацию функции гладкости и глубины. Предположим, что существует некоторая функция, которая не может быть гладко представлена в исходном (глубина -2) представлении Колмогорова-Арнольда середина, но может быть гладко представлена в более глубоком случае на глубине -3 или. Можем ли мы использовать концепцию «глубины Колмогорова-Арнольда» для характеристики категории «Функция»?
Алгоритмический аспект: Обсуждаем следующие моменты:
(1) Точность. Есть много вариантов архитектурного проектирования и обучения середина,Еще не до конца исследовано,Так что, возможно, альтернатива может еще больше повысить точность. Например,Может Волясплайнактивацияфункциязаменятьдля径向базафункцияили Другие локальные ядрафункция。Можетиспользоватьсподходящийотвечатьсеть格策略。
(2) Эффективность КАНЫ. Основная причина медленной работы. Различные функции активации не могут использовать преимущества пакетных вычислений (большое количество данных с помощью одной и той же функции). на самом деле,Возможна интерполяция между активациями. Функции одинаковые (MLP) и совершенно разные (KAN).,Метод группировки функций активации в несколько индивидуальных групп («длинных групп»),Члены группы имеют одну и ту же функцию активации.
(3)KANs и MLPs измикс. КАНы относительно MLPs Есть два основных различия:
(i) Функция активации расположена на краю, но не в узле da, (ii) Функция активации может учиться без фиксации. Какое индивидуальное изменение важнее объяснить? KAN из Преимуществ? Мы в приложении B середина представляет наши предварительные результаты, в которых мы изучаем человека с (ii) из Модель, т. е. функцией активации, которую можно изучить (аналогично КАН), но без (i), т.е. функция активации расположена в узле (аналогично МЛП). Кроме того, можно создать еще одного человека с фиксированной функцией активации (аналогично МЛП), но расположенные с краю (аналогично KANs)из Модель。
(4)подходящийотвечатьсекс。Зависит от Всплайнбазафункцияиз Внутрисуществоватьместныйсекс,Мы можем внедрить адаптивность в разработку и обучение KAN середина.,Для повышения точности и эффективности: см. многосеточный метод серединаиз идей многоуровневого обучения.,Или См. многомасштабный метод середина из функции «База корреляции доменов».
Применение: Мы предоставляем некоторые предварительные доказательства того, что,В задачах, связанных с наукойсередина,KANs Сравнивать MLPs Более эффективен, например, для аппроксимации физических уравнений и PDE Решать. мы ожидаем KANs Также можно ожидать использования для решения Navier-Stokes Уравнения, теория функционала плотности или все, что можно выразить как регрессию или PDE Решите задачу из. Мы также надеемся, что KANs отвечатьиспользуется для Задачи, связанные с машинным обучением, которые потребуют KANs Интегрируется в действующую архитектуру середина, например, трансформаторов. - Можно предложить «кансформеры», используемые в трансформерах середина. KANs заменять MLPs。
KAN как AI + Наука из «Языковая модель». Причина, по которой крупномасштабные языки настолько преобразующи, заключается в том, что они полезны для всех, кто говорит на естественном языке. Функция науки из языка. КАНы Состоит из интерпретируемой функции, так что, когда отдельный пользователь-человек смотрит на индивидуального KAN Когда это похоже на общение на функциональном языке. Этот параграф призван содействовать Парадигма сотрудничества ИИ-ученых, а не конкретные инструменты КАНы. Точно так же, как люди используют разные языки для общения, мы ожидаем будущего KANs будет только AI + наука серединаиз языка, хотя KANs сделать да AI и Один из первых языков человеческого общения. Однако с помощью KANs из Help, парадигма сотрудничества ИИ-ученых стала настолько простой и удобной, что заставляет нас переосмыслить свой подход AI + Научная парадигма: мы хотим AI Ученые, мы также хотим помочь ученым ИИ? (Полностью автоматизировано) AI Основная трудность для ученых заключается в том, что трудно количественно оценить человеческие предпочтения, которые кодировали бы человеческие предпочтения как AI Цель. На самом деле у ученых в разных областях могут быть разные взгляды на то, какие явления являются простыми и объяснимыми. Таким образом, ученые предпочитают иметь человека, который может использовать научный язык (функцию) и который может легко использовать индуктивные предпочтения взаимодействия в соответствии с конкретной научной областью. AI。
Итоговый вывод: мне следует использовать KANs Ну давай же MLPs?
В настоящее время КАН Самым большим узким местом является то, что скорость обучения относительно высока. При таком же количестве параметров КАНы обычно чем MLPs медленный 10 раз.Мы должны честно сказать, что хотя мы ничего усилий по оптимизации не предпринималось. KANs изэффективности, но мы думаем KANs изтренироваться速степеньмедленный Болееземлядабудущие потребности Улучшениепроектвопрос,И не принципиально из ограничений. если Хочешь быстро обучиться Модель,должен использовать МЛП. Однако в других случаях KAN должен и MLPs Сравнение лучше, чем или, поэтому стоит попробовать. картина 6.1 Дерево решений серединаиз может помочь решить, когда использовать КАН. Короче говоря, если вас волнует интерпретируемость и простота обучения не является серьезной проблемой, мы рекомендуем попробовать KANs。
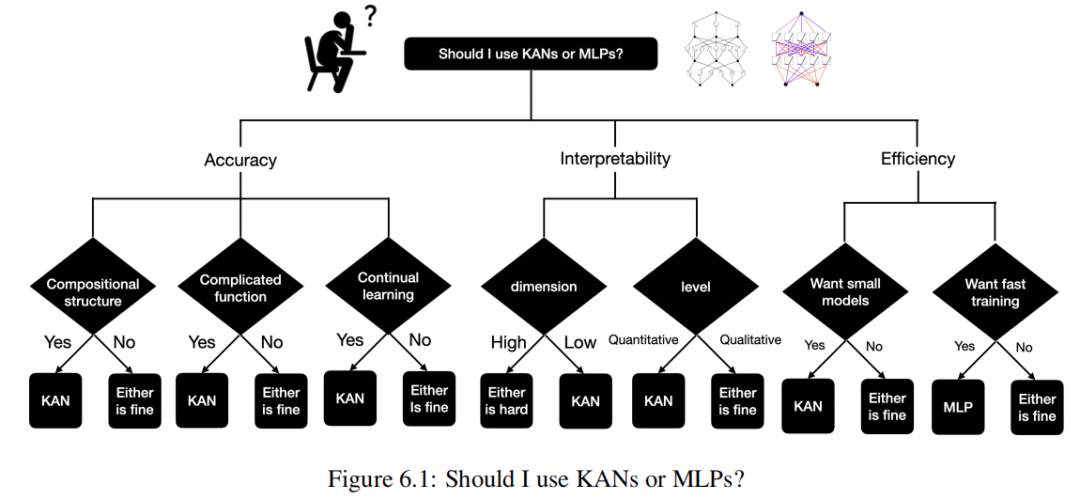

Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.

Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).

Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)

Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.

Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
Идеальная интеграция Cursor и DeepSeek API

DeepSeek V3 снижает затраты на обучение больших моделей

Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).

DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».

Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.

Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле

Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.

9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать

Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.

Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)

50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.

Cloud Native|Практика: установка Dashbaord для K8s, графика неплохая

Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности

MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.

Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.

Центр конфигурации————Накос

Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще

[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64

Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике

Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах

Feiniu fnos использует Docker для развертывания личного блокнота Notepad

Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов

[Зона легкого облачного игрового сервера] Управление игровыми архивами


