Используйте LSTM для прогнозного анализа временных рядов осадков [совместное использование кода, руководство для няни! 】
Прогнозирование временных рядов осадков с использованием LSTM
В этой статье будет рассказано, как использовать сеть долгосрочной краткосрочной памяти (LSTM) для прогнозирования временных рядов осадков. LSTM — это рекуррентная нейронная сеть (RNN), специально разработанная для обработки долгосрочных зависимостей в данных последовательности.
Годовые данные об осадках могут быть весьма нестабильными. В отличие от температуры, которая часто демонстрирует четкие сезонные тенденции, количество осадков как временной ряд может быть весьма неустойчивым. Сеть LSTM способна собирать и запоминать информацию в длинных последовательностях, поэтому она очень подходит для данных временных рядов осадков.
Принцип ЛСТМ
В отличие от традиционных нейронных сетей с прямой связью, сети LSTM имеют блоки памяти, которые могут хранить и обновлять информацию. Это позволяет им изучать закономерности и зависимости во входных последовательностях.
Ключевыми компонентами блока LSTM являются входной вентиль, вентиль забывания и выходной вентиль. Эти ворота контролируют поток информации в ячейку и из нее, позволяя LSTM выборочно сохранять или удалять информацию. Более того, состояние клетки действует как долговременная память, сохраняя соответствующую информацию на протяжении всего времени.

Преимущества LSTM для прогнозирования осадков
Сеть LSTM имеет следующие преимущества при прогнозировании временных рядов осадков:
- «Учет долгосрочных зависимостей»:LSTMБлок памяти делаетсеть Способность запоминать и использовать информацию из более ранних временных шагов.,Это имеет решающее значение для моделирования моделей осадков с долгосрочными зависимостями.
- «Обработка последовательностей переменной длины»:Временные ряды осадков часто имеют разную длину из-за нерегулярных интервалов между измерениями.。LSTMсетьможет обрабатывать такие последовательности переменной длины,Ввод фиксированного размера не требуется.
- «Нелинейное моделирование»:LSTMсеть Можно изучить сложные нелинейные взаимосвязи между входными объектами и характером осадков.,Это позволяет фиксировать сложные зависимости, которые могут игнорироваться традиционными статистическими моделями.
Постройте модель LSTM
Введение данных
Вот многополосные глобальные данные об осадках (ERA5)
from utils import plot
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import numpy as np
import xarray as xr
file_name='D:/Onedrive/Acdemic/DL_grace/data/train/prcp.tif'
ds=xr.open_dataset(file_name)
data = ds['band_data'][7]
fig = plt.figure()
proj = ccrs.Robinson() #ccrs.Robinson()ccrs.Mollweide()Mollweide()
ax = fig.add_subplot(111, projection=proj)
levels = np.linspace(0, 0.25, num=9)
plot.one_map_flat(data, ax, levels=levels, cmap="RdBu", mask_ocean=False, add_coastlines=True, add_land=True, colorbar=True, plotfunc="pcolormesh")
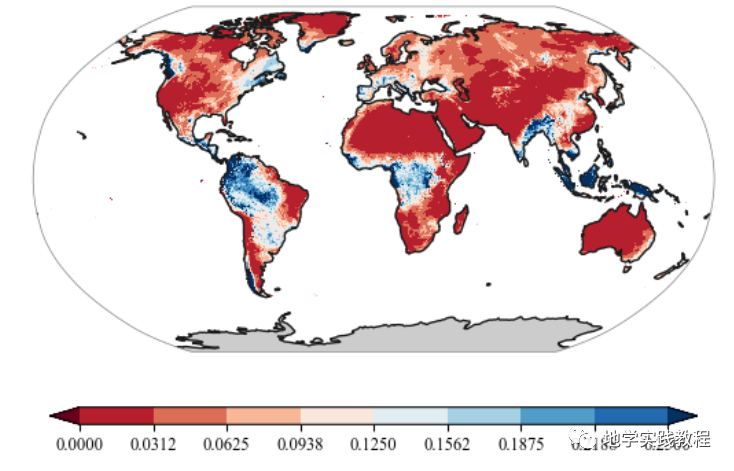
Вышеупомянутое использует функциюone_map_flatнарисованный,Если вы хотите научиться,Вы можете обратиться к предыдущему твиту: Нарисуйте карту в стиле природы одним щелчком мыши.
Я написал функцию для рисования глобальной карты в стиле Nature одним щелчком мыши.
Импортировать необходимую среду
import torch
import torch as t
import numpy as np
import torch.nn as nn
import torch.optim as optim
from torchnet import meter
import xarray as xr
import rioxarray as rxr
Проверьте, доступен ли графический процессор
torch.cuda.is_available()
Если у вас нет среды глубокого обучения, обратитесь к предыдущему твиту: Создание среды глубокого обучения с нуля.
Не знаете основных принципов глубокого обучения? Вы можете обратиться к предыдущему резюме ресурса:
Чтение данных и предварительная обработка
Преобразование данных в тензоры PyTorch и нормализация
precipitation_data = rxr.open_rasterio('D:/Onedrive/Acdemic/DL_grace/data/train/prcp.tif').values
# Преобразовать данные в PyTorch Тензор
precipitation_data = torch.tensor(precipitation_data, dtype=torch.float32)
precipitation_mean = torch.mean(precipitation_data, 0)
precipitation_std = torch.std(precipitation_data, 0)
precipitation = (precipitation_data - precipitation_mean) / precipitation_std
precipitation_re = precipitation.reshape(183,-1).transpose(0,1)
Это глобальные осадки на поверхности суши, поэтому удалите растры с пустыми океанами.
# Создайте 2D-матрицу
import random
matrix = torch.mean(torch.stack([torch.mean(precipitation_re, 1)], 1), 1).flatten()
# Установите элементы NaN в матрице на 0.
matrix[torch.isnan(matrix)] = 0
# Получить индекс всех элементов, которые не являются NaN
non_negative_indices = torch.nonzero(matrix)
precipitation_re = precipitation_re[non_negative_indices.flatten(), :]
Определение сетевой связи
Определите глобальные параметры:
class Config(object):
t0 = 155 #155
t1 = 12
t = t0 + t1
train_num = 8000 #8
validation_num = 1000 #1
test_num = 1000 #1
in_channels = 1
batch_size = 500 #500 NSE 0.75
lr = .0005 # learning rate
epochs = 100
Определите загрузку набора данных и многое другое:
import torch
import matplotlib.pyplot as plt
import numpy as np
from torch.utils.data import Dataset
class time_series_decoder_paper(Dataset):
"""synthetic time series dataset from section 5.1"""
def __init__(self,t0=120,N=4500,dx=None,dy=None,transform=None):
"""
Args:
t0: previous t0 data points to predict from
N: number of data points
transform: any transformations to be applied to time series
"""
self.t0 = t0
self.N = N
self.dx = dx
self.dy = dy
self.transform = None
# time points
#self.x = torch.cat(N*[torch.arange(0,t0+24).type(torch.float).unsqueeze(0)])
self.x = dx
self.fx = dy
# self.fx = torch.cat([A1.unsqueeze(1)*torch.sin(np.pi*self.x[0,0:12]/6)+72 ,
# A2.unsqueeze(1)*torch.sin(np.pi*self.x[0,12:24]/6)+72 ,
# A3.unsqueeze(1)*torch.sin(np.pi*self.x[0,24:t0]/6)+72,
# A4.unsqueeze(1)*torch.sin(np.pi*self.x[0,t0:t0+24]/12)+72],1)
# add noise
# self.fx = self.fx + torch.randn(self.fx.shape)
self.masks = self._generate_square_subsequent_mask(t0)
# print out shapes to confirm desired output
print("x: ",self.x.shape,
"fx: ",self.fx.shape)
def __len__(self):
return len(self.fx)
def __getitem__(self,idx):
if torch.is_tensor(idx):
idx = idx.tolist()
sample = (self.x[idx,:,:], #self.x[idx,:]
self.fx[idx,:],
self.masks)
if self.transform:
sample=self.transform(sample)
return sample
def _generate_square_subsequent_mask(self,t0):
mask = torch.zeros(Config.t,Config.t)
for i in range(0,Config.t0):
mask[i,Config.t0:] = 1
for i in range(Config.t0,Config.t):
mask[i,i+1:] = 1
mask = mask.float().masked_fill(mask == 1, float('-inf'))#.masked_fill(mask == 1, float(0.0))
return mask
Определить теги контекстной последовательности
import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn.functional as F
class CausalConv1d(torch.nn.Conv1d):
def __init__(self,
in_channels,
out_channels,
kernel_size,
stride=1,
dilation=1,
groups=1,
bias=True):
super(CausalConv1d, self).__init__(
in_channels,
out_channels,
kernel_size=kernel_size,
stride=stride,
padding=0,
dilation=dilation,
groups=groups,
bias=bias)
self.__padding = (kernel_size - 1) * dilation
def forward(self, input):
return super(CausalConv1d, self).forward(F.pad(input, (self.__padding, 0)))
class context_embedding(torch.nn.Module):
def __init__(self,in_channels=Config.in_channels,embedding_size=256,k=5):
super(context_embedding,self).__init__()
self.causal_convolution = CausalConv1d(in_channels,embedding_size,kernel_size=k)
def forward(self,x):
x = self.causal_convolution(x)
return torch.tanh(x)
Определить сеть LSTM
class LSTM_Time_Series(torch.nn.Module):
def __init__(self,input_size=2,embedding_size=256,kernel_width=9,hidden_size=512):
super(LSTM_Time_Series,self).__init__()
self.input_embedding = context_embedding(input_size,embedding_size,kernel_width)
self.lstm = torch.nn.LSTM(embedding_size,hidden_size,batch_first=True)
self.fc1 = torch.nn.Linear(hidden_size,1)
def forward(self,x,y):
"""
x: the time covariate
y: the observed target
"""
# concatenate observed points and time covariate
# (B,input size + covariate size,sequence length)
# z = torch.cat((y.unsqueeze(1),x.unsqueeze(1)),1)
z_obs = torch.cat((y.unsqueeze(1),x.unsqueeze(1)),1)
if isLSTM:
z_obs = torch.cat((y, x),1)
# input_embedding returns shape (B,embedding size,sequence length)
z_obs_embedding = self.input_embedding(z_obs)
# permute axes (B,sequence length, embedding size)
z_obs_embedding = self.input_embedding(z_obs).permute(0,2,1)
# all hidden states from lstm
# (B,sequence length,num_directions * hidden size)
lstm_out,_ = self.lstm(z_obs_embedding)
# input to nn.Linear: (N,*,Hin)
# output (N,*,Hout)
return self.fc1(lstm_out)
Загрузка данных
Случайным образом выбирайте данные из всех данных для обучения, проверки и прогнозирования.
Здесь 8:1:1
from torch.utils.data import DataLoader
import random
random.seed(0)
random_indices = random.sample(range(non_negative_indices.shape[0]), Config.train_num)
random_indices1 = random.sample(range(non_negative_indices.shape[0]), Config.validation_num)
random_indices2 = random.sample(range(non_negative_indices.shape[0]), Config.test_num)
dx = torch.stack([torch.cat(Config.train_num*[torch.arange(0,Config.t).type(torch.float).unsqueeze(0)]).cuda()], 1)
dx1 = torch.stack([torch.cat(Config.validation_num*[torch.arange(0,Config.t).type(torch.float).unsqueeze(0)]).cuda()], 1)
dx2 = torch.stack([torch.cat(Config.test_num*[torch.arange(0,Config.t).type(torch.float).unsqueeze(0)]).cuda()], 1)
train_dataset = time_series_decoder_paper(t0=Config.t0,N=Config.train_num,dx=dx ,dy=precipitation_re[np.array([random_indices]).flatten(),0:Config.t].unsqueeze(1))
validation_dataset = time_series_decoder_paper(t0=Config.t0,N=Config.validation_num,dx=dx1,dy=precipitation_re[np.array([random_indices1]).flatten(),0:Config.t].unsqueeze(1))
test_dataset = time_series_decoder_paper(t0=Config.t0,N=Config.test_num,dx=dx2,dy=precipitation_re[np.array([random_indices2]).flatten(),0:Config.t].unsqueeze(1))
Загрузить данные в графический процессор
criterion = torch.nn.MSELoss()
train_dl = DataLoader(train_dataset,batch_size=Config.batch_size,shuffle=True, generator=torch.Generator(device='cpu'))
validation_dl = DataLoader(validation_dataset,batch_size=Config.batch_size, generator=torch.Generator(device='cpu'))
test_dl = DataLoader(test_dataset,batch_size=Config.batch_size, generator=torch.Generator(device='cpu'))
Определить функцию потерь
criterion_LSTM = torch.nn.MSELoss()
Загрузить модель в графический процессор
LSTM = LSTM_Time_Series().cuda()
Модельное обучение
определениеtrain_epochВ ожидании тренировки、проверять、Тестовая функция
def Dp(y_pred,y_true,q):
return max([q*(y_pred-y_true),(q-1)*(y_pred-y_true)])
def Rp_num_den(y_preds,y_trues,q):
numerator = np.sum([Dp(y_pred,y_true,q) for y_pred,y_true in zip(y_preds,y_trues)])
denominator = np.sum([np.abs(y_true) for y_true in y_trues])
return numerator,denominator
def train_epoch(LSTM,train_dl,t0=Config.t0):
LSTM.train()
train_loss = 0
n = 0
for step,(x,y,_) in enumerate(train_dl):
x = x.cuda()
y = y.cuda()
optimizer.zero_grad()
output = LSTM(x,y)
loss = criterion(output.squeeze()[:,(Config.t0-1):(Config.t0+Config.t1-1)],y.cuda()[:,0,Config.t0:])
loss.backward()
optimizer.step()
train_loss += (loss.detach().cpu().item() * x.shape[0])
n += x.shape[0]
return train_loss/n
def eval_epoch(LSTM,validation_dl,t0=Config.t0):
LSTM.eval()
eval_loss = 0
n = 0
with torch.no_grad():
for step,(x,y,_) in enumerate(train_dl):
x = x.cuda()
y = y.cuda()
output = LSTM(x,y)
loss = criterion(output.squeeze()[:,(Config.t0-1):(Config.t0+Config.t1-1)],y.cuda()[:,0,Config.t0:])
eval_loss += (loss.detach().cpu().item() * x.shape[0])
n += x.shape[0]
return eval_loss/n
def test_epoch(LSTM,test_dl,t0=Config.t0):
with torch.no_grad():
predictions = []
observations = []
LSTM.eval()
for step,(x,y,_) in enumerate(train_dl):
x = x.cuda()
y = y.cuda()
output = LSTM(x,y)
for p,o in zip(output.squeeze()[:,(Config.t0-1):(Config.t0+Config.t1-1)].cpu().numpy().tolist(),y.cuda()[:,0,Config.t0:].cpu().numpy().tolist()):
predictions.append(p)
observations.append(o)
num = 0
den = 0
for y_preds,y_trues in zip(predictions,observations):
num_i,den_i = Rp_num_den(y_preds,y_trues,.5)
num+=num_i
den+=den_i
Rp = (2*num)/den
return Rp
Начать обучение
train_epoch_loss = []
eval_epoch_loss = []
Rp_best = 30
isLSTM = True
optimizer = torch.optim.Adam(LSTM.parameters(), lr=Config.lr)
for e,epoch in enumerate(range(Config.epochs)):
train_loss = []
eval_loss = []
l_train = train_epoch(LSTM,train_dl)
train_loss.append(l_train)
l_eval = eval_epoch(LSTM,validation_dl)
eval_loss.append(l_eval)
Rp = test_epoch(LSTM,test_dl)
if Rp_best > Rp:
Rp_best = Rp
with torch.no_grad():
print("Epoch {}: Train loss={} \t Eval loss = {} \t Rp={}".format(e,np.mean(train_loss),np.mean(eval_loss),Rp))
train_epoch_loss.append(np.mean(train_loss))
eval_epoch_loss.append(np.mean(eval_loss))
Результат такой, как показано на рисунке, здесь 100 эпох.
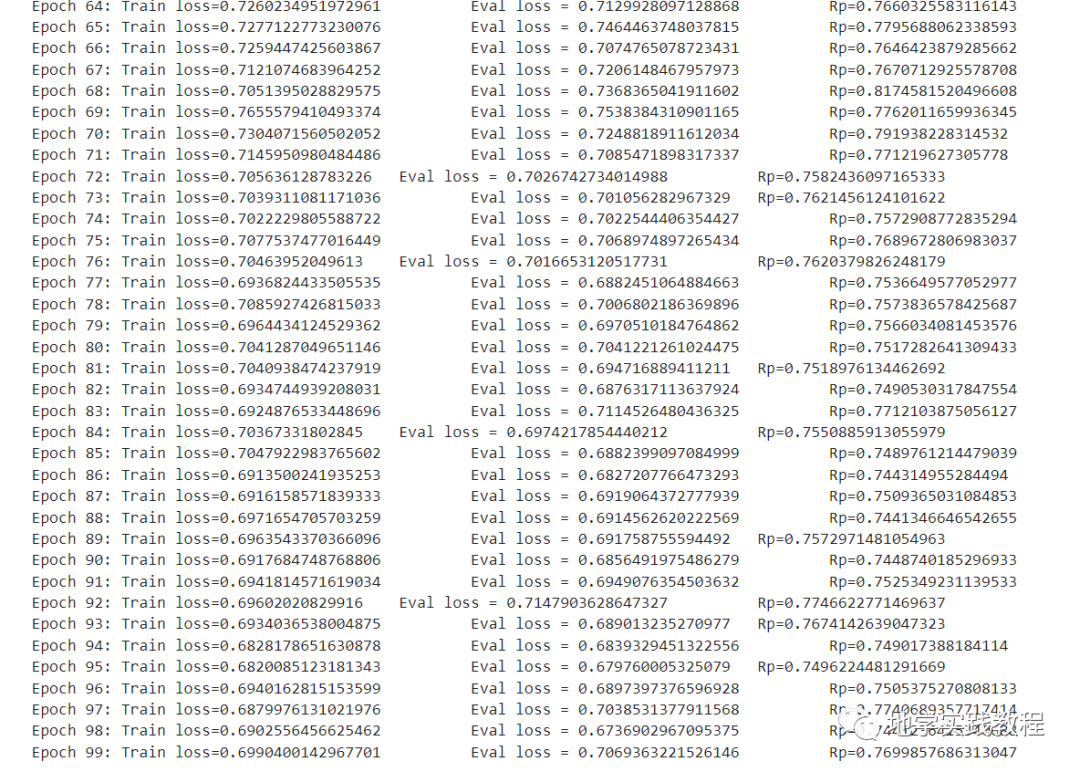
image-20230807223945852
Результаты показывают, что эффект прогнозирования по-прежнему хорош во временных рядах:
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
n_plots = 5
t0=120
with torch.no_grad():
LSTM.eval()
for step,(x,y,_) in enumerate(test_dl):
x = x.cuda()
y = y.cuda()
output = LSTM(x,y)
if step > n_plots:
break
with torch.no_grad():
plt.figure(figsize=(10,10))
plt.plot(x[1, 0].cpu().detach().squeeze().numpy(),y[1].cpu().detach().squeeze().numpy(),'g--',linewidth=3)
plt.plot(x[1, 0, Config.t0:].cpu().detach().squeeze().numpy(),output[1,(Config.t0-1):(Config.t0+Config.t1-1),0].cpu().detach().squeeze().numpy(),'b--',linewidth=3)
plt.xlabel("x",fontsize=20)
plt.legend(["$[0,t_0+24)_{obs}$","$[t_0,t_0+24)_{predicted}$"])
plt.show()
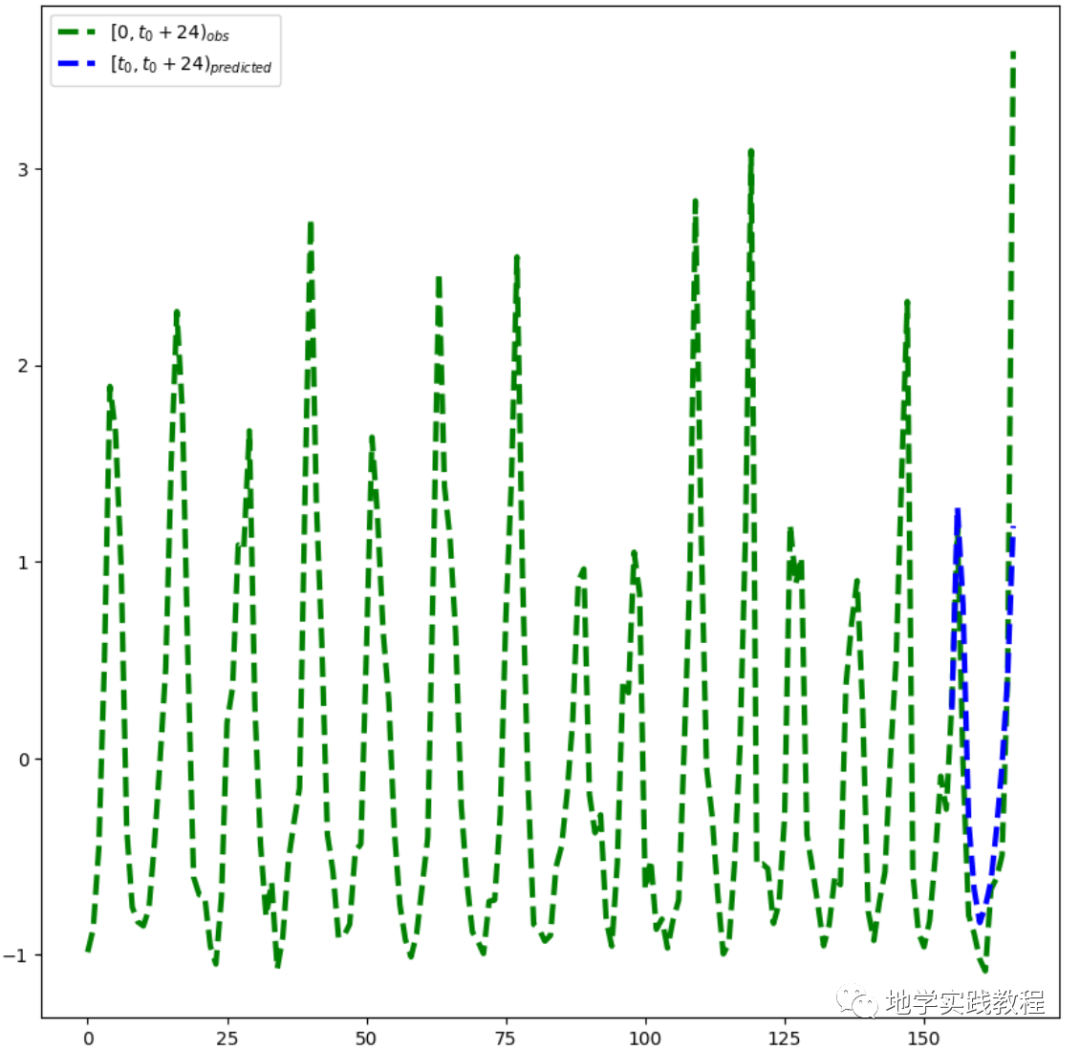
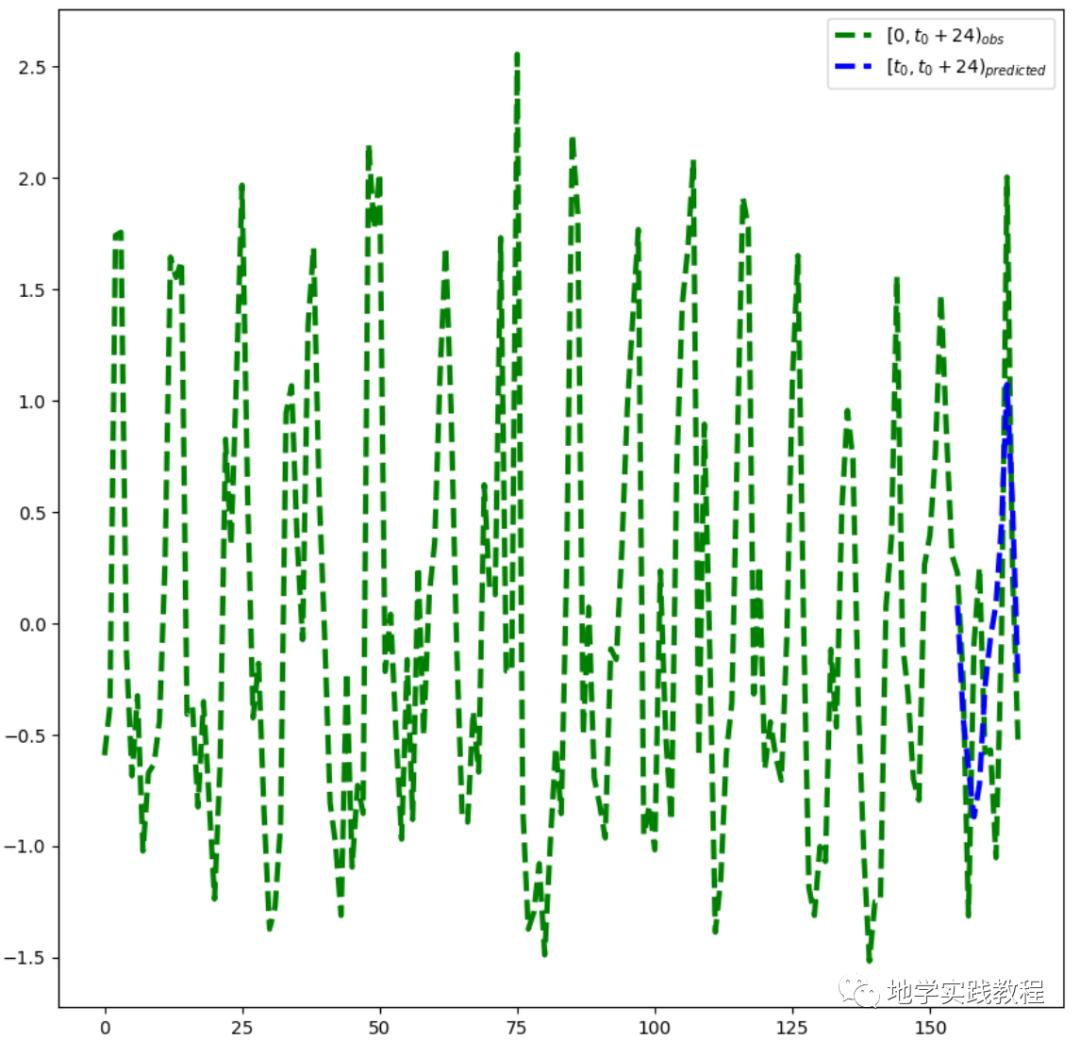
Далее выполните все проверки на тестовом наборе:
matrix = torch.empty(0).cuda()
obsmat = torch.empty(0).cuda()
with torch.no_grad():
LSTM.eval()
predictions = []
observations = []
for step,(x,y,attention_masks) in enumerate(test_dl):
# if step == 8:
# break
output = LSTM(x.cuda(),y.cuda())
matrix = torch.cat((matrix, output.cuda()))
obsmat = torch.cat((obsmat, y.cuda()))
pre = matrix.cpu().detach().numpy()
obs = obsmat.cpu().detach().numpy()
# libraries
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# data
df = pd.DataFrame({
'obs': obs[:, 0, Config.t0:Config.t].flatten(),
'pre': pre[:, Config.t0:Config.t, 0].flatten()
})
df
Результаты визуализации:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
from matplotlib import rcParams
from statistics import mean
from sklearn.metrics import explained_variance_score,r2_score,median_absolute_error,mean_squared_error,mean_absolute_error
from scipy.stats import pearsonr
# Загрузка данных (PS: слишком много исходных данных, выборка 10 000)
# По умолчанию столбец csv/xlsx считывается в DataFrame.
config = {"font.family":'Times New Roman',"font.size": 16,"mathtext.fontset":'stix'}
#df = df.sample(5000)
# используется для расчета показателей
x = df['obs']; y = df['pre']
rcParams.update(config)
BIAS = mean(x - y)
MSE = mean_squared_error(x, y)
RMSE = np.power(MSE, 0.5)
R2 = pearsonr(x, y).statistic
adjR2 = 1-((1-r2_score(x,y))*(len(x)-1))/(len(x)-Config.in_channels-1)
MAE = mean_absolute_error(x, y)
EV = explained_variance_score(x, y)
NSE = 1 - (RMSE ** 2 / np.var(x))
# Рассчитать плотность рассеяния
xy = np.vstack([x, y])
z = stats.gaussian_kde(xy)(xy)
idx = z.argsort()
x, y, z = x.iloc[idx], y.iloc[idx], z[idx]
# Примерка (если будете менять на МК, то делайте сами) по методу наименьших квадратов
def slope(xs, ys):
m = (((mean(xs) * mean(ys)) - mean(xs * ys)) / ((mean(xs) * mean(xs)) - mean(xs * xs)))
b = mean(ys) - m * mean(xs)
return m, b
k, b = slope(x, y)
regression_line = []
for a in x:
regression_line.append((k * a) + b)
# Рисуя, вы можете сами регулировать цвета и т. д.
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
fig,ax=plt.subplots(figsize=(8,6),dpi=300)
scatter=ax.scatter(x, y, marker='o', c=z*100, edgecolors=None ,s=15, label='LST',cmap='Spectral_r')
cbar=plt.colorbar(scatter,shrink=1,orientation='vertical',extend='both',pad=0.015,aspect=30,label='frequency')
plt.plot([-30,30],[-30,30],'black',lw=1.5) # Нарисована линия 1:1, цвет линии черный, ширина линии 0,8.
plt.plot(x,regression_line,'red',lw=1.5) # Линия регрессии между прогнозируемыми и измеренными данными
plt.axis([-30,30,-30,30]) # Установить диапазон линии
plt.xlabel('OBS',family = 'Times New Roman')
plt.ylabel('PRE',family = 'Times New Roman')
plt.xticks(fontproperties='Times New Roman')
plt.yticks(fontproperties='Times New Roman')
plt.text(-1.8,1.75, '$N=%.f$' % len(y), family = 'Times New Roman') # Положение текста необходимо настроить в соответствии с диапазоном размеров x и y.
plt.text(-1.8,1.50, '$R^2=%.3f$' % R2, family = 'Times New Roman')
plt.text(-1.8,1.25, '$NSE=%.3f$' % NSE, family = 'Times New Roman')
plt.text(-1.8,1, '$RMSE=%.3f$' % RMSE, family = 'Times New Roman')
plt.xlim(-2,2) # Установите диапазон отображения оси X
plt.ylim(-2,2) # Установите диапазон отображения оси Y
plt.show()
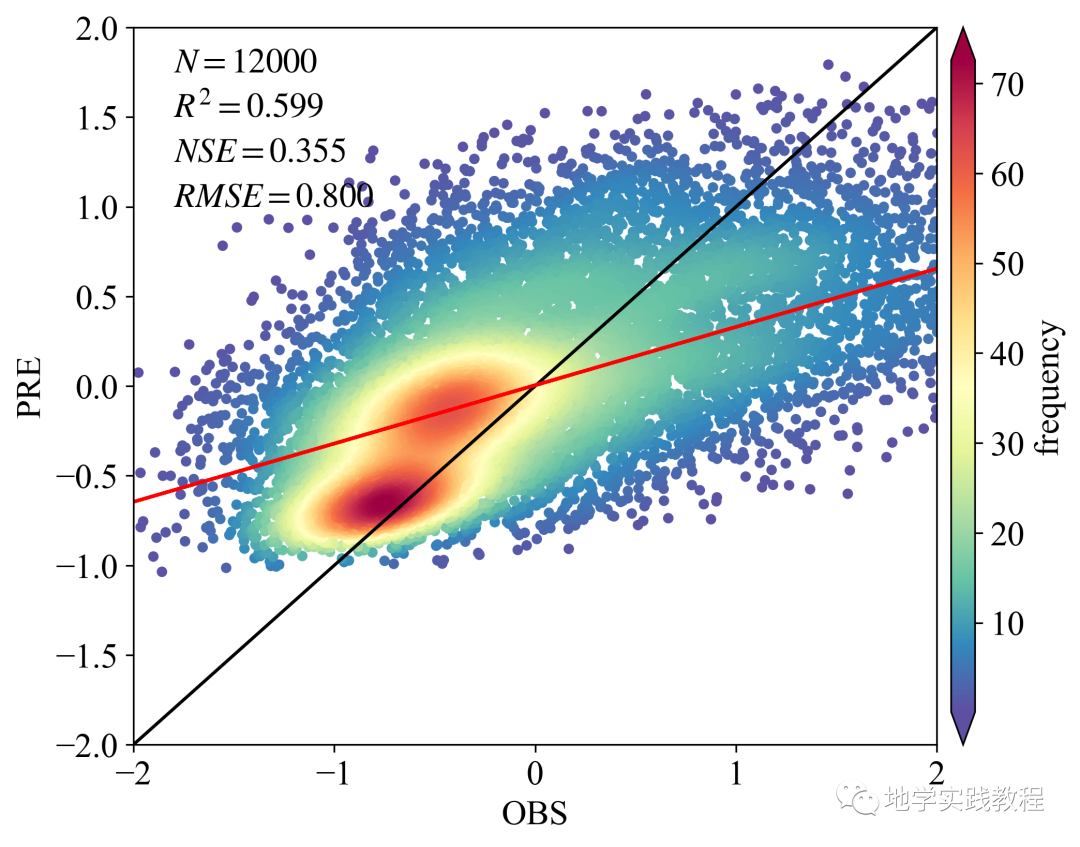
Если вы хотите узнать, как сделать приведенное выше изображение, вы можете обратиться к предыдущему твиту: Python рисует диаграмму плотности рассеяния.
Грубые результаты по-прежнему хорошие, и в модели не проводилась корректировка параметров. Попробуйте изменить lr, размер пакета, функцию потерь, эпохи и т. д. для более глубокой настройки параметров, что улучшит результаты.

Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.

Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).

Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)

Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.

Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
Идеальная интеграция Cursor и DeepSeek API

DeepSeek V3 снижает затраты на обучение больших моделей

Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).

DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».

Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.

Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле

Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.

9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать

Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.

Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)

50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.

Cloud Native|Практика: установка Dashbaord для K8s, графика неплохая

Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности

MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.

Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.

Центр конфигурации————Накос

Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще

[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64

Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике

Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах

Feiniu fnos использует Docker для развертывания личного блокнота Notepad

Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов

[Зона легкого облачного игрового сервера] Управление игровыми архивами


