Оригинал / Чжу Цзицянь

1. Сценарные случаи

В сети сообщества может потребоваться запросить набор вершин, смежных с каждой вершиной, аналогично сценарию запроса того, кто находится рядом с человеком.

В графе Spark данные соседних вершин исходной вершины можно получить с помощью функции CollectNeighbors.

Ниже приведен пример для иллюстрации. Сначала создайте график на основе набора вершин и ребер.

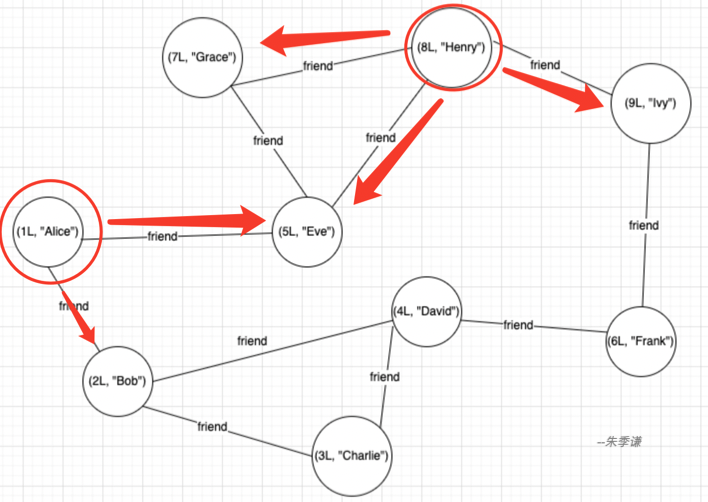
Множество вершин этого графа —

(1L, "Alice"),
(2L, "Bob"),
(3L, "Charlie"),
(4L, "David"),
(5L, "Eve"),
(6L, "Frank"),
(7L, "Grace"),
(8L, "Henry"),
(9L, "Ivy")

Набор ребер ——

Edge(1L, 2L, "friend"),
Edge(1L, 5L, "friend"),
Edge(2L, 3L, "friend"),
Edge(2L, 4L, "friend"),
Edge(3L, 4L, "friend"),
Edge(4L, 6L, "friend"),
Edge(5L, 7L, "friend"),
Edge(5L, 8L, "friend"),
Edge(6L, 9L, "friend"),
Edge(7L, 8L, "friend"),
Edge(8L, 9L, "friend")

На основе приведенных выше вершин и ребер создайте RDD вершин и RDD ребер соответственно, а затем создайте граф Graph через Graph(vertices, Edges, defaultVertex), код выглядит следующим образом:

val conf = new SparkConf().setMaster("local[*]").setAppName("graphx")
val ss = SparkSession.builder().config(conf).getOrCreate()

// Создать вершину RDD
val vertices = ss.sparkContext.parallelize(Seq(
  (1L, "Alice"),
  (2L, "Bob"),
  (3L, "Charlie"),
  (4L, "David"),
  (5L, "Eve"),
  (6L, "Frank"),
  (7L, "Grace"),
  (8L, "Henry"),
  (9L, "Ivy")
))


// Создать ребро RDD
val edges = ss.sparkContext.parallelize(Seq(
  Edge(1L, 2L, "friend"),
  Edge(1L, 5L, "friend"),
  Edge(2L, 3L, "friend"),
  Edge(2L, 4L, "friend"),
  Edge(3L, 4L, "friend"),
  Edge(4L, 6L, "friend"),
  Edge(5L, 7L, "friend"),
  Edge(5L, 8L, "friend"),
  Edge(6L, 9L, "friend"),
  Edge(7L, 8L, "friend"),
  Edge(8L, 9L, "friend")
))

val graph = Graph(vertices, edges, null)

После успешного создания графа вы можете использовать метод CollectNeighbors для получения данных о соседних вершинах, связанных с каждой вершиной, на основе существующего графа — —

val neighborVertexs = graph.mapVertices{
  case (id,(label)) => (label)
}.collectNeighbors(EdgeDirection.Either)

Полученный файл nextVertexs представляет собой RDD типа VertexRDD[Array[(VertexId, VD)]]. Вы можете распечатать и просмотреть его с помощью nextVertexs.foreach(println). Вы обнаружите, что данные содержат структуру каждой [вершины, кортежа]. Обратите внимание: посмотрите, вы, вероятно, догадались, что RDD, полученный с помощью nextVertexs, на самом деле представляет собой данные, в которых каждая вершина связана с соседним кортежем набора вершин ——.

(5,[Lscala.Tuple2;@bb793d7)
(8,[Lscala.Tuple2;@6d5786e6)
(1,[Lscala.Tuple2;@398cb9ea)
(9,[Lscala.Tuple2;@61c4eeb2)
(2,[Lscala.Tuple2;@d7d0256)
(6,[Lscala.Tuple2;@538f0156)
(7,[Lscala.Tuple2;@77a17e3d)
(3,[Lscala.Tuple2;@1be2a4fb)
(4,[Lscala.Tuple2;@1e0153f9)

Это можно дополнительно проверить, развернув и распечатав данные в кортеже, а затем проверив их с помощью следующего кода: сначала установите раздел в один раздел с помощью объединения (1). Трудно определить порядок печати при печати нескольких разделов. Затем просмотрите каждый элемент в RDD через foreach. Структура элемента здесь такая: (5,[Lscala.Tuple2;@bb793d7), x._1 представляет вершину 5, x._2 представляет [Lscala.Tuple2;@bb793d7, поскольку это так. Tuple, дальше можно обходить и печатать, т.е. x._2.foreach(y => {...})——

neighborVertexs.coalesce(1).foreach(x => {
    print("Вершина:" + x._1 + "связанный набор соседних вершин->{" )
    var str = "";
    x._2.foreach(y => {
      str += y + ","})
    print(str.substring(0, str.length - 1 ) +"}")
    println()
})

Вы можете наблюдать конечный результат печати——

вершина：8связанный набор соседних вершин->{(5,Eve),(7,Grace),(9,Ivy)}
вершина：1связанный набор соседних вершин->{(2,Bob),(5,Eve)}
вершина：9связанный набор соседних вершин->{(6,Frank),(8,Henry)}
вершина：2связанный набор соседних вершин->{(1,Alice),(3,Charlie),(4,David)}
вершина：3связанный набор соседних вершин->{(2,Bob),(4,David)}
вершина：4связанный набор соседних вершин->{(2,Bob),(3,Charlie),(6,Frank)}
вершина：5связанный набор соседних вершин->{(1,Alice),(7,Grace),(8,Henry)}
вершина：6связанный набор соседних вершин->{(4,David),(9,Ivy)}
вершина：7связанный набор соседних вершин->{(5,Eve),(8,Henry)}

С помощью графа в начале статьи проверьте, что соседними вершинами, связанными с вершиной 1, являются (2, Боб), (5, Ева), что верно; смежными вершинами, связанными с вершиной 8, являются (5, Ева), ( 7, Грейс), (9, Айви), верно. Другие проверки соответствуют ситуации, приведенной ниже. Видно, что данные о соседних вершинах, связанных с каждой вершиной в сети, действительно можно получить через метод CollectNeighbors(EdgeDirection.Either).

2. Анализ принципов функционального кода

Выше приведен пример использования ассоциации вершин со смежными вершинами. Далее давайте проанализируем исходный код CollectNeighbors(EdgeDirection.Either). Эта функция реализует сбор информации о вершинах-соседях ——.

def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexId, VD)]] = {
  val nbrs = edgeDirection match {
    //Объединяем соседние вершины, исходящая степень которых указывает на эту вершину, и соседние вершины, чья исходящая степень указывает на эту вершину.
    case EdgeDirection.Either =>
      graph.aggregateMessages[Array[(VertexId, VD)]](
        ctx => {
          ctx.sendToSrc(Array((ctx.dstId, ctx.dstAttr)))
          ctx.sendToDst(Array((ctx.srcId, ctx.srcAttr)))
        },
        (a, b) => a ++ b, TripletFields.All)
    //Объединяем соседние вершины, на которые указывает исходящая степень этой вершины
    case EdgeDirection.In =>
      graph.aggregateMessages[Array[(VertexId, VD)]](
        ctx => ctx.sendToDst(Array((ctx.srcId, ctx.srcAttr))),
        (a, b) => a ++ b, TripletFields.Src)
    //Инградация агрегации указывает на соседние вершины этой вершины
    case EdgeDirection.Out =>
      graph.aggregateMessages[Array[(VertexId, VD)]](
        ctx => ctx.sendToSrc(Array((ctx.dstId, ctx.dstAttr))),
        (a, b) => a ++ b, TripletFields.Dst)
    case EdgeDirection.Both =>
      throw new SparkException("collectEdges does not support EdgeDirection.Both. Use" +
        "EdgeDirection.Either instead.")
  }
  graph.vertices.leftJoin(nbrs) { (vid, vdata, nbrsOpt) =>
    nbrsOpt.getOrElse(Array.empty[(VertexId, VD)])
  }
} // end of collectNeighbor

Эта функция использует match для сопоставления переключателей в стиле Java. Среди них последний, EdgeDirection.Both, больше не поддерживается, поэтому я не буду его здесь объяснять. три, которые все еще полезны.

Давайте воспользуемся изображением для иллюстрации. Если есть изображение, указывающее на следующее:

Edge(2L, 1L), Edge(2L, 4L), Edge(3L, 2L), Edge(2L, 5L),

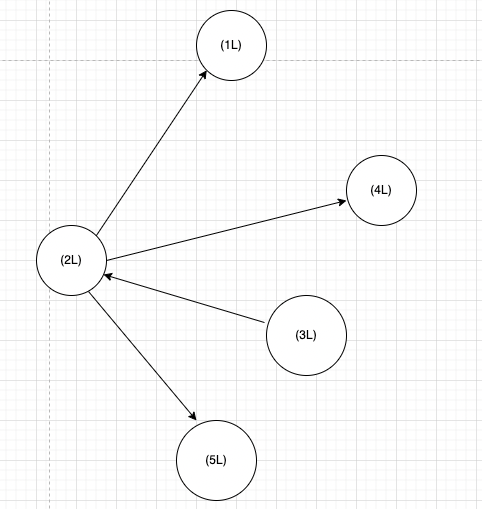
• EdgeDirection.Either представляет соседей исходящей и входной степени этой вершины. Если эта вершина равна 2, то она получит соседние вершины, включая (1, 4, 3, 5). Этот параметр означает, что пока с вершиной связаны ребра 2 степени, они будут собраны в соседние вершины.
• EdgeDirection.In представляет соседа, указывающего на эту вершину, то есть соседа по степени этой вершины. Если эта вершина равна 2, и только 3 соседние вершины в графе указывают на 2, то соседние вершины, полученные вершиной 2, включают (3).
• EdgeDirection.Out представляет соседнюю вершину, на которую указывает исходящая степень этой вершины. Если эта вершина равна 2 и граф указывает из вершины 2 на соседние вершины, мы получим (1, 4, 5).

Видно, что параметры в функции CollectNeighbors(EdgeDirection.Either), которая связывает вершины с соседними вершинами, могут получать соседние вершины в различных ситуациях на основе этих параметров.

Здесь CollectNeighbors(EdgeDirection.Either) используется для иллюстрации основной логики функции — —

 graph.aggregateMessages[Array[(VertexId, VD)]](
        ctx => {
          ctx.sendToSrc(Array((ctx.dstId, ctx.dstAttr)))
          ctx.sendToDst(Array((ctx.srcId, ctx.srcAttr)))
        },
        (a, b) => a ++ b, TripletFields.All)

Этот код выполняет агрегацию, а это означает, что будут обработаны все ребра графа.

В графе существует реберная структура, называемая тройкой. Эта структура состоит из следующих трех частей:

1. Исходная вершина: начальная точка или исходный узел ребра графа.
2. Целевая вершина: конечная точка или целевой узел ребра графа.
3. Атрибут ребра: значение атрибута на ребре, соединяющем исходную вершину и целевую вершину.

существоватьgraph.aggregateMessages[Array[(VertexId, VD)]]( ctx => {...}) В функции агрегирования статистика агрегирования выполняется на основе троек.

Эта агрегатная функция имеет два параметра, первый параметр — функция (ctx). => { ... }, который определяет, как каждая вершина отправляет сообщения соседним вершинам.

Обратите внимание, что ctx здесь — это именно тройной объект. На основе этого объекта вы можете получить следующую информацию:

• ctx.srcId：获取源вершина的ID。
• ctx.srcAttr：获取源вершина的属性。
• ctx.dstId：获取目标вершина的ID。
• ctx.dstAttr：获取目标вершина的属性。

Будучи тройным объектом, который знает исходную вершину и целевую вершину, ctx подобен почтальону, отвечающему за отправку сообщений вершинам с обеих сторон.

1. Функция ctx.sendToSrc(Array((ctx.dstId, ctx.dstAttr))), где вершина A используется в качестве целевой вершины, соседний узел B является исходной вершиной, а объект ctx объединяет идентификатор вершины и атрибуты. целевой вершины B. Кортеж из (ctx.dstId, ctx.dstAttr) в качестве сообщения исходной вершине A, A сохранит полученное сообщение, чтобы знать, что у него есть сосед B в случае EdgeDirection. Либо ненаправленное ребро.

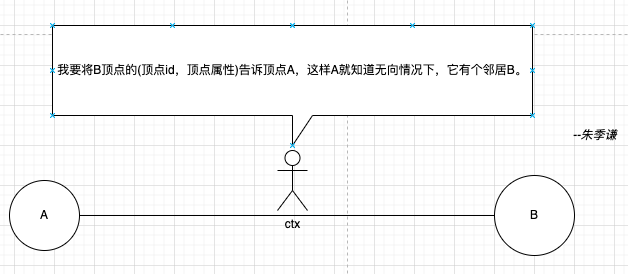
2. Функция ctx.sendToDst(Array((ctx.srcId, ctx.srcAttr))), тогда A становится исходной вершиной, C становится целевой вершиной, а объект ctx объединит идентификатор вершины и атрибуты исходной вершины A Кортеж (ctx.dstId, ctx.dstAttr) отправляется в исходную вершину B в виде сообщения. B сохранит полученное сообщение в формате массива Array((ctx.dstId, ctx.dstAttr)), чтобы в будущем B знал, что у него есть сосед A в случае EdgeDirection. Либо ненаправленное ребро.

Здесь ctx.sendToDst() использует Array((ctx.dstId, ctx.dstAttr))Отправить в форме массива,Это удобно для спины(a, b) => a ++ b Операция функции слияния, наконец, каждая вершина может объединить полученные ею массивы соседних вершин в большой массив, то есть все соседние вершины собираются в один массив и возвращаются.

Существует также перечисление TripletFields, которое необходимо понять:

TripletFields.All указывает, что эта вершина будет объединять исходные и целевые вершины для отправки сообщений вершин.

TripletFields.Src указывает, что эта вершина объединяет только сообщения вершин, отправленные из исходной вершины.

TripletFields.Dst означает, что эта вершина объединяет только сообщения вершин, отправленные целевой вершиной.

Параметр EdgeDirection.Either соответствует TripletFields.All, что указывает на то, что все исходные вершины, полученные этой вершиной, и сообщения вершин, отправленные целевой вершиной, необходимо агрегировать.

Далее пришло время выполнить агрегацию ——

Во всем графе будет много объектов ctx, похожих на персонажа почтальона. Пока эти объекты обрабатываются, каждая вершина будет получать информацию о соседней вершине, передаваемую через объект ctx.

Например, сообщение соседа, отправленное объектом ctx, полученным A, выглядит следующим образом:

Массив((B,свойство))

Массив((C,свойство))

Массив((D,свойство))

......

В это время,Вы можете использовать вершину A в качестве ключа группировки.,внутри группы Массив((B,свойство))、Массив((C,свойство))、Массив((D,свойство)) объединяются в одну группу, то есть через (а, b) => a ++ b Объедините все данные группы в большой массив {(B, атрибут), (C, атрибут), (D, атрибут)}. Ключом этой группы является вершина A, которая получает сообщение соседа, отправленное каждым объектом ctx. .

После агрегирования каждой вершины возвращается nbrs, каждый элемент RDD, то есть (вершина, атрибут вершины, массив (соседняя вершина)) — —

val nbrs = edgeDirection match {
  case EdgeDirection.Either =>
    graph.aggregateMessages[Array[(VertexId, VD)]](
      ctx => {
        ctx.sendToSrc(Array((ctx.dstId, ctx.dstAttr)))
        ctx.sendToDst(Array((ctx.srcId, ctx.srcAttr)))
      },
      (a, b) => a ++ b, TripletFields.All)
		......  
}

Затем установите левое соединение между rdd вершин исходного графа и результатом агрегации nbrs и верните новый VertexRDD Объект, в котором каждая вершина сопровождается информацией о ее соседях. Если вершина не имеет информации о соседях (в nbrs Соответствующей записи в ) нет), для представления соседей используется пустой массив.

graph.vertices.leftJoin(nbrs) { (vid, vdata, nbrsOpt) =>
  nbrsOpt.getOrElse(Array.empty[(VertexId, VD)])
}

Наконец, полученный RDD вершин, связанных с соседними вершинами, такой, как напечатан выше:

(5,[Lscala.Tuple2;@bb793d7) вершина5展开邻居вершина=> вершина：5связанный набор соседних вершин->{(1,Alice),(7,Grace),(8,Henry)} (8,[Lscala.Tuple2;@6d5786e6) вершина8展开邻居вершина=> вершина：8связанный набор соседних вершин->{(5,Eve),(7,Grace),(9,Ivy)} (1,[Lscala.Tuple2;@398cb9ea) вершина1展开邻居вершина=> вершина：1связанный набор соседних вершин->{(2,Bob),(5,Eve)} (9,[Lscala.Tuple2;@61c4eeb2) вершина9展开邻居вершина=> вершина：9связанный набор соседних вершин->{(6,Frank),(8,Henry)} (2,[Lscala.Tuple2;@d7d0256) вершина2展开邻居вершина=> вершина：2связанный набор соседних вершин->{(1,Alice),(3,Charlie),(4,David)} (6,[Lscala.Tuple2;@538f0156) вершина6展开邻居вершина=> вершина：6связанный набор соседних вершин->{(4,David),(9,Ivy)} (7,[Lscala.Tuple2;@77a17e3d) вершина7展开邻居вершина=> вершина：7связанный набор соседних вершин->{(5,Eve),(8,Henry)} (3,[Lscala.Tuple2;@1be2a4fb) вершина3展开邻居вершина=> вершина：3связанный набор соседних вершин->{(2,Bob),(4,David)} (4,[Lscala.Tuple2;@1e0153f9) вершина4展开邻居вершина=> вершина：4связанный набор соседних вершин->{(2,Bob),(3,Charlie),(6,Frank)}