1. Разница между механизмом внимания и механизмом самовнимания

Разница между механизмом внимания и механизмом самовнимания

Традиционный механизм внимания возникает между элементами Target и всеми элементами Source.

Проще говоря, для расчета весов в механизме Attention требуется участие Target. То есть в модели «Кодер-декодер» для расчета веса внимания требуется не только скрытое состояние в кодировщике, но и скрытое состояние в декодере.

Self-Attention：

Это не механизм внимания между оператором ввода и оператором вывода, а механизм внимания, который возникает между элементами внутри оператора ввода или между элементами внутри оператора вывода.

Например, при расчете весовых параметров в Трансформере для преобразования текстового вектора в соответствующий KQV достаточно выполнить соответствующую матричную операцию в Источнике, а информация в Цели не используется.

2. Цель внедрения механизма самовнимания

Входные данные, получаемые нейронной сетью, представляют собой множество векторов разного размера, и между различными векторами существует определенная связь. Однако во время реального обучения взаимосвязь между этими входными данными не может быть полностью использована, что приводит к крайне плохим результатам обучения модели. Например, проблемы машинного перевода (проблемы с последовательностью, машина решает, сколько тегов использовать), проблемы разметки частей речи (один вектор соответствует одному тегу), проблемы семантического анализа (несколько векторов соответствуют одному тегу). ) и другие проблемы с обработкой текста.

Чтобы решить проблему, заключающуюся в том, что полностью связанные нейронные сети не могут установить корреляцию для нескольких связанных входных данных, для решения этой проблемы используется механизм самоконтроля. Механизм самоконтроля фактически хочет, чтобы машина замечала корреляцию между различными частями целого. вход. .

3. Подробное объяснение внимания к себе.

Входные данные представляют собой набор векторов, выходные данные также представляют собой набор векторов. Входные данные представляют собой вектор длины N (N можно изменить), а выходные данные также являются вектором длины N.

3.1 Одиночный выход

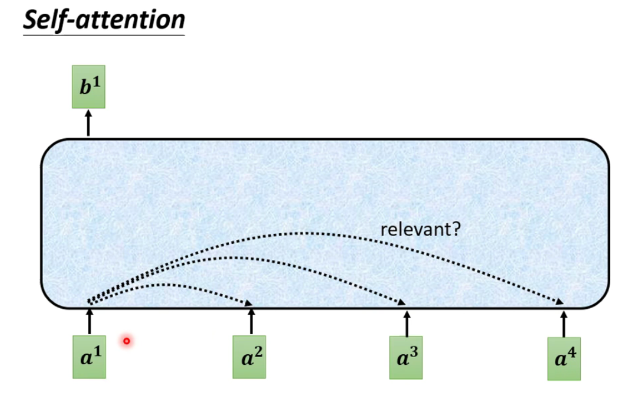
Для каждого входного вектора a после синей части выводится вектор b. Этот вектор b получается путем рассмотрения влияния всех входных векторов на a1. Имеются четыре соответствующих вектора слов a.

В качестве примера ниже взят вывод b1.

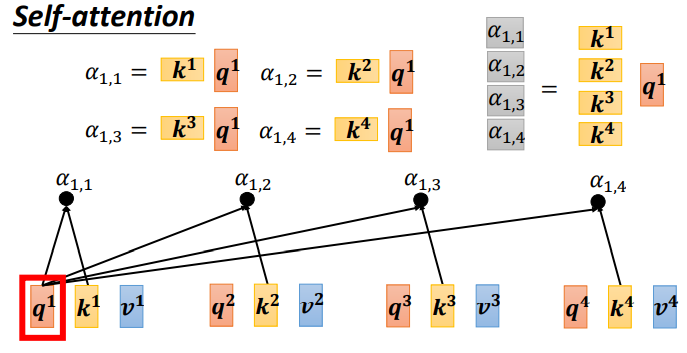
Во-первых, как вычислить степень корреляции между каждым вектором в последовательности и a1, существует два метода:

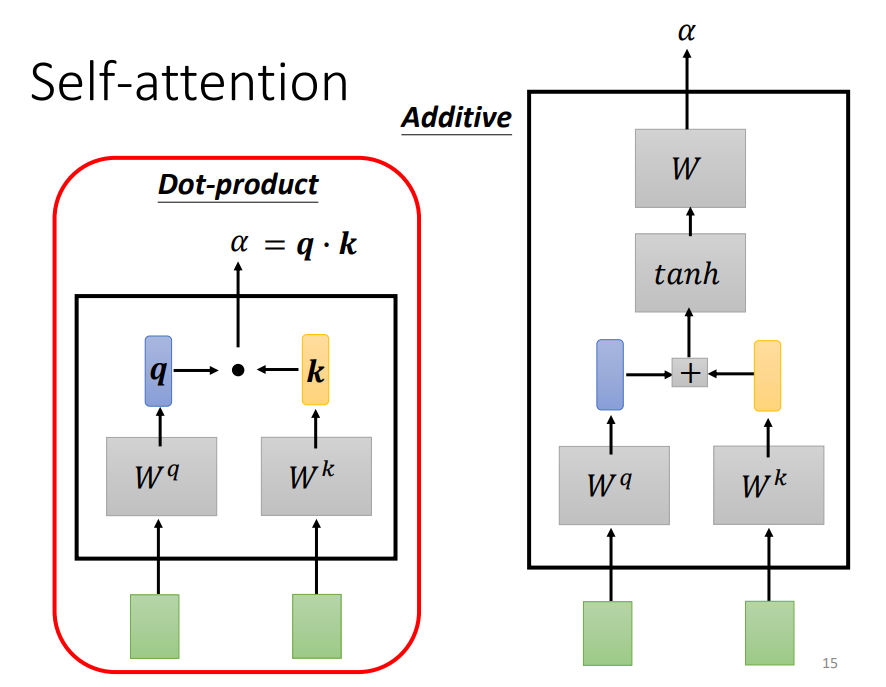
Метод скалярного произведения заключается в умножении двух векторов на разные матрицы w, чтобы получить q и k, и скалярном произведении, чтобы получить α.

Зеленые части на рисунке выше — это входные векторы a1 и a2. Серые Wq и Wk — это весовые матрицы, которые необходимо научиться обновлять. Используйте a1, чтобы умножить Wq, чтобы получить вектор q, а затем используйте a2 и Wk, чтобы получить вектор q. умножьте его, чтобы получить значение k. Наконец, используйте q и k, чтобы выполнить скалярное произведение и получить α. α также представляет степень корреляции между двумя векторами.

Механизм аддитивной модели в правой части рисунка выше заключается в том, что входной вектор умножается на матрицу весов, затем складывается, а затем проецируется в новое функциональное пространство с помощью tanh, а затем умножается на матрицу весов для получения окончательный результат.

Каждый α (также называемый оценкой внимания) может быть вычислен, q называется запросом, а k называется ключом.

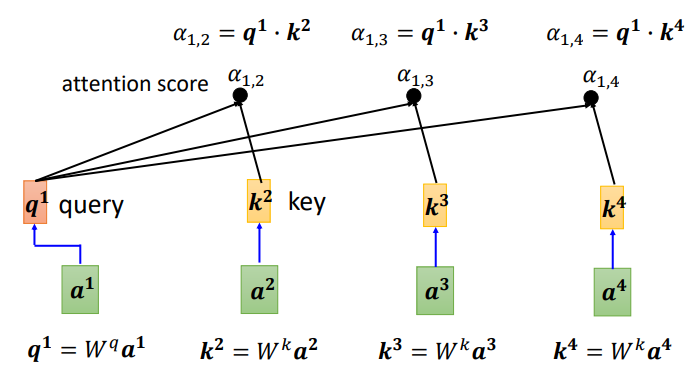
Кроме того, вы также можете рассчитать корреляцию между a1 и самим собой. После получения степени корреляции между каждым вектором и a1 используйте softmax для расчета распределения внимания. Таким образом, вы можете нормализовать степень корреляции. посмотрите, какие векторы сумма a1 наиболее актуальна.

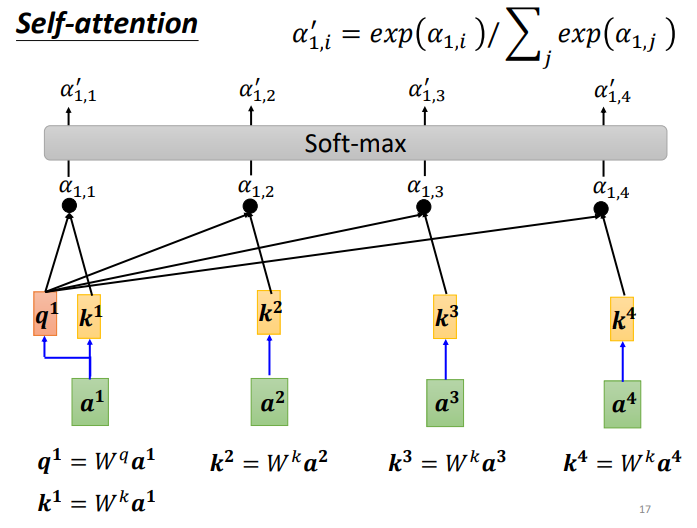
Далее нам нужно извлечь важную информацию в последовательности на основе α’:

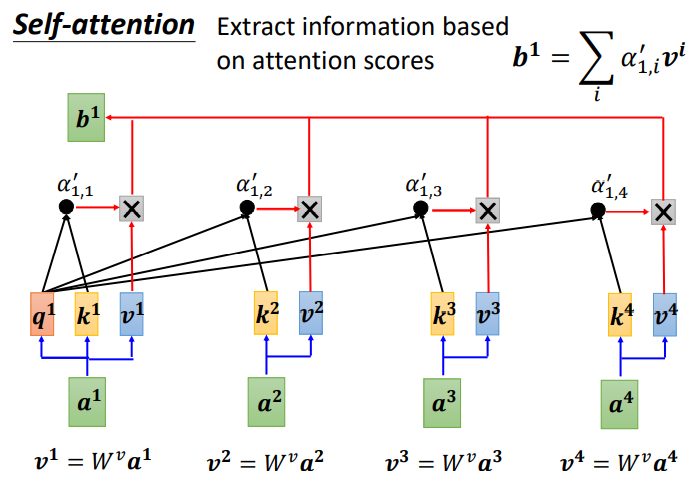
Сначала найдите v, v — ключевое значение, v вычисляется так же, как q и k, а входные данные a умножаются на весовую матрицу W. После получения v умножьте его на соответствующее α ', а затем вычислите каждый v после умножения α' и получите результат b1.

Если корреляция между a1 и a2 относительно высока, α1,2' относительно велика, то выходной сигнал b1 может быть ближе к v2, то есть показатель внимания определяет компонент вектора в результате;

3.2 Матричная форма

Используйте матричные операции, чтобы выразить генерацию b1:

Step 1: Создать матричную форму q, k, v

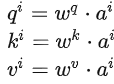
Записано в матричной форме:

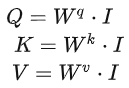
Поместите 4 входа a в матрицу

, эта матрица имеет 4 столбца, а именно от a1 до a4,

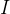
Умножьте соответствующую матрицу весов W, чтобы получить соответствующие матрицы Q, K и V, которые представляют запрос, ключ и значение соответственно.

Три W — это параметры, которые нам нужно изучить.

Step 2：Используйте полученные Q и K для расчета корреляции между каждыми двумя входными векторами, то есть вычисляйте значение внимания α, Существует множество способов вычисления α, обычно используется умножение точек.

Сначала для q1, умножив его на матрицу K, склеенную от k1 до k4, получим

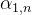
склеенная матрица.

Аналогично, от q1 до q4 также можно объединить в матрицу Q и напрямую умножить на матрицу K:

Формула:

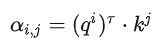
Форма матрицы:

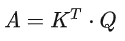
Каждое значение в матрице A записывает размер внимания α соответствующих двух входных векторов, а A' представляет собой матрицу, нормализованную softmax.

Step 3：доступныйA'иV,Вычислите выходной вектор b слоя самообслуживания, соответствующий каждому входному вектору a:

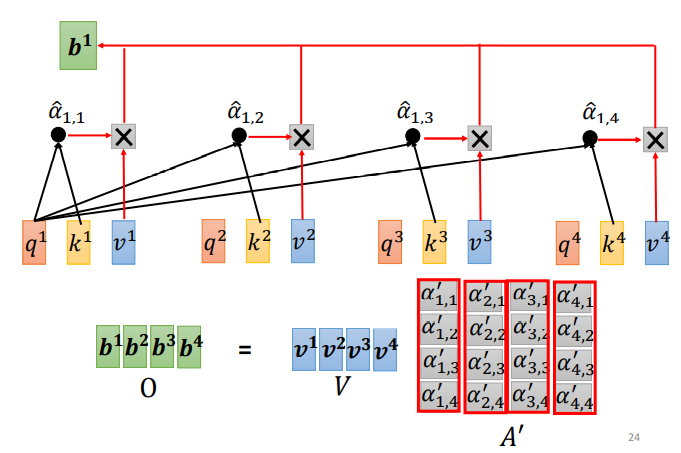
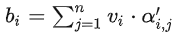
Записано в матричной форме:

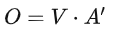
Подводя итог процессу работы самообслуживания, вход — I, а выход — O:

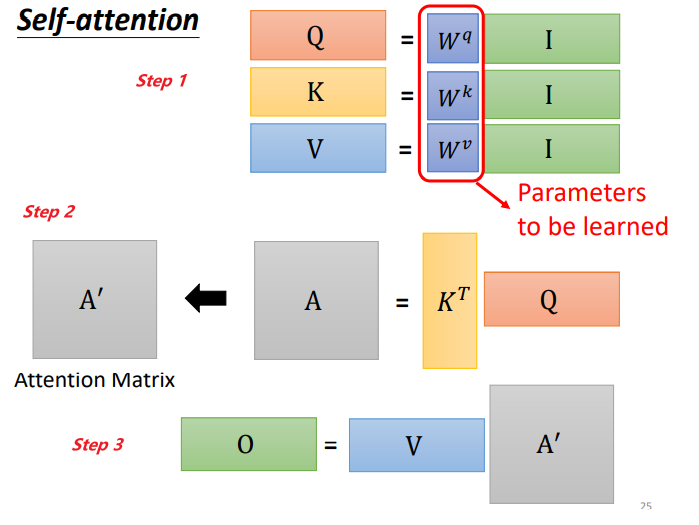
Матрицы Wq, Wk и Wv — это параметры, которые необходимо изучить.

Четыре、Внимание к себе с несколькими головками

Многоголовочное самообслуживание, усовершенствованная версия самообслуживания, механизм самообслуживания с несколькими головками

Поскольку существует много разных форм корреляции и много разных определений, иногда не может быть только одного q, а должно быть несколько q, и разные q отвечают за разные типы корреляций.

Для 1 входа а

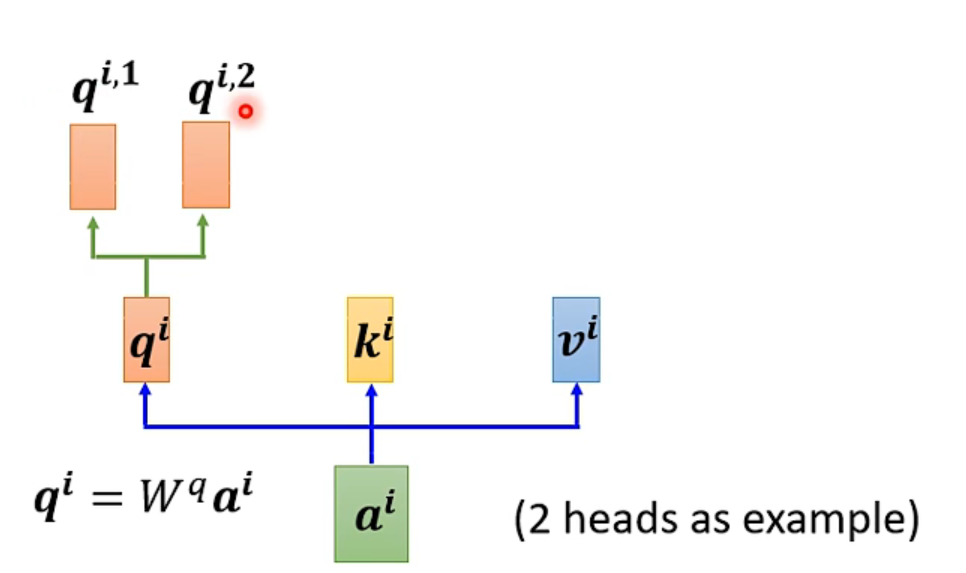
Сначала, как указано выше, умножьте весовую матрицу W на a, чтобы получить ее, а затем умножьте ее на два разных W, чтобы получить две разные единицы: i представляет позицию, а 1 и 2 представляют q-ю позицию.

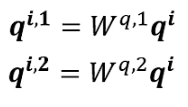
На картинке выше две головы, а это значит, что эта задача имеет две разные корреляции.

Точно так же должно быть несколько k и v. Два k и v вычисляются так же, как q. Сначала вычисляются ki и vi, а затем умножаются на две разные весовые матрицы.

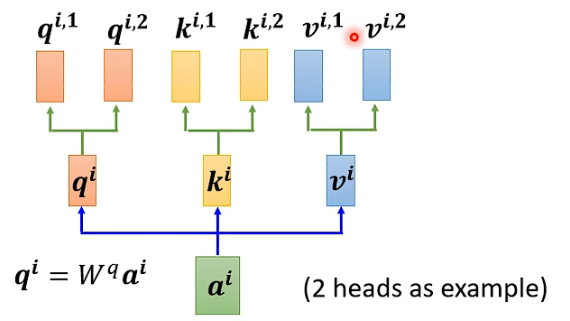
То же самое касается нескольких входных векторов, каждый из которых имеет несколько головок:

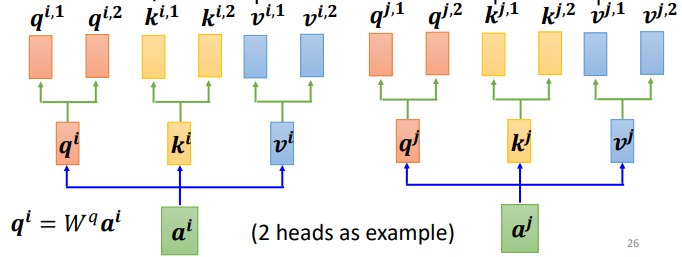
Как заняться самообслуживанием после вычисления q, k, v?

Это то же самое, что и процесс, упомянутый выше, за исключением того, что тип 1 выполняется вместе, а тип 2 выполняется вместе, вычисляются два независимых процесса и два b.

Для 1:

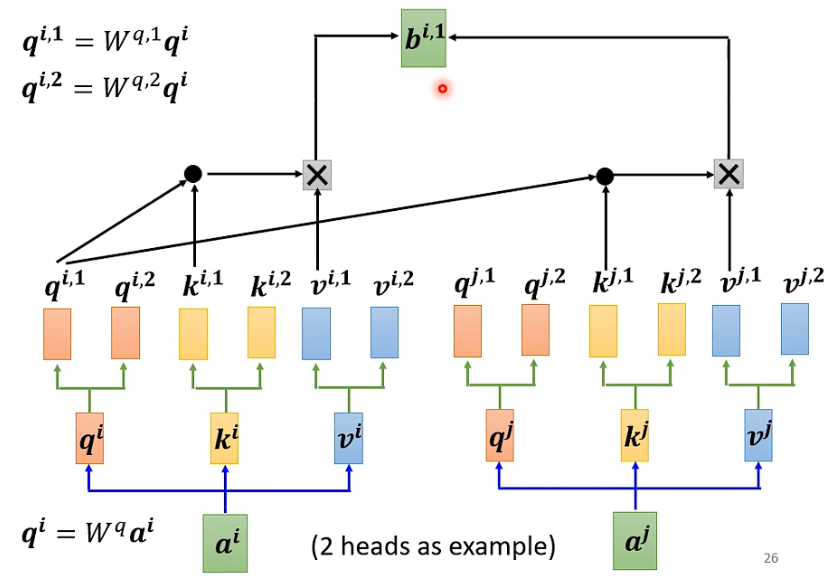
Для двоих:

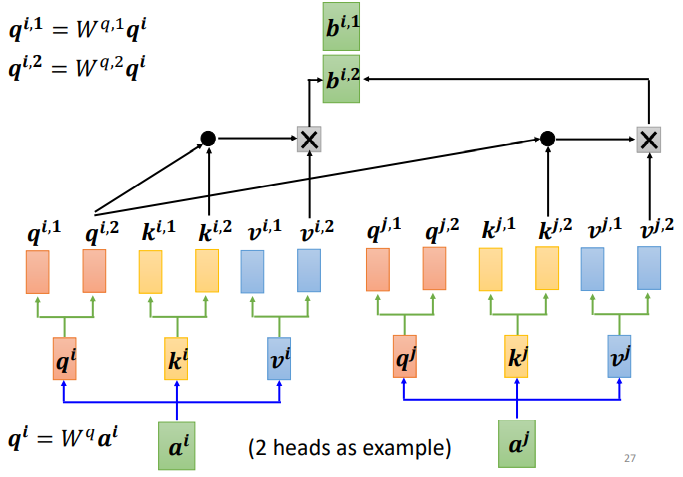
Это всего лишь пример двух голов. То же самое, если головок несколько. B рассчитывается отдельно.

пять、Позиционное кодирование

При тренировке внимания информация о положении фактически отсутствует, и нет никакой разницы между «до» и «после». Упомянутые выше a1, a2 и a3 не представляют порядок ввода, а относятся только к количеству входных векторов. В отличие от RNN, существует очевидный последовательный порядок. Например, в задаче перевода для «машинного обучения» машинное обучение вводится последовательно. Ввод внимания к себе вводится одновременно, а вывод генерируется и выводится одновременно.

Как отразить информацию о местоположении в Self-Attention? Просто используйте позиционное кодирование

Если ai добавляется к ei, это будет отражать информацию о местоположении.

Длина вектора задается искусственно или может быть обучена на основе данных.

6. Разница между вниманием к себе и RNN

Основное различие между вниманием к себе и RNN заключается в следующем:

1. Самообслуживание может учитывать все входные данные, в то время как RNN, похоже, учитывает только предыдущий входной сигнал (слева). Но этой проблемы можно избежать при использовании двунаправленной RNN.

2. Самообслуживание позволяет легко учитывать долгосрочные входные данные, в то время как самые ранние входные данные RNN становится сложнее учитывать, поскольку они обрабатываются многими уровнями сетей.

3. Самовнимание можно рассчитывать параллельно, но между разными слоями РНС существует последовательность.

1. Самообслуживание может учитывать все входные данные, в то время как RNN, похоже, учитывает только предыдущий входной сигнал (слева). Но этой проблемы можно избежать при использовании двунаправленной RNN.

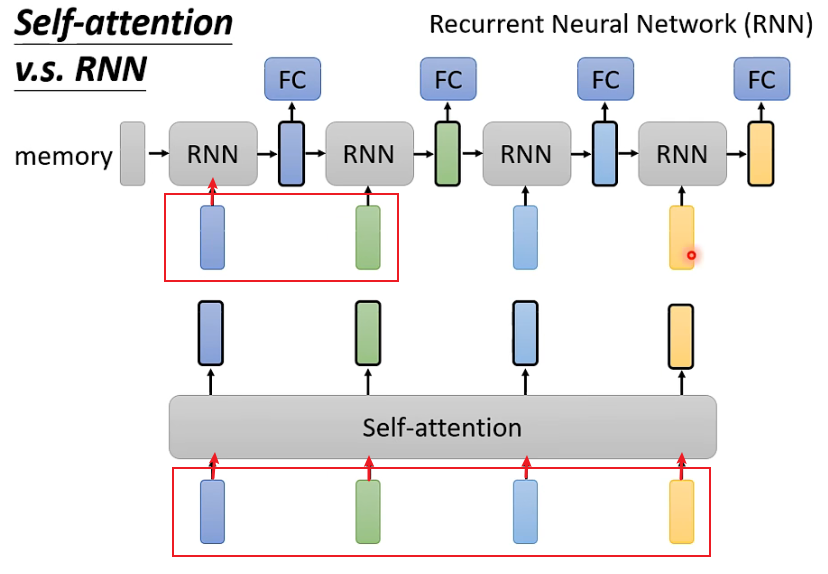
Например, для первого RNN учитывается только синий вход, а входы после зеленого и зеленого не учитываются, тогда как Self-Attention учитывает все 4 входа.

2. Самообслуживание позволяет легко учитывать долгосрочные входные данные, в то время как самые ранние входные данные RNN становится сложнее учитывать, поскольку они обрабатываются многими уровнями сетей.

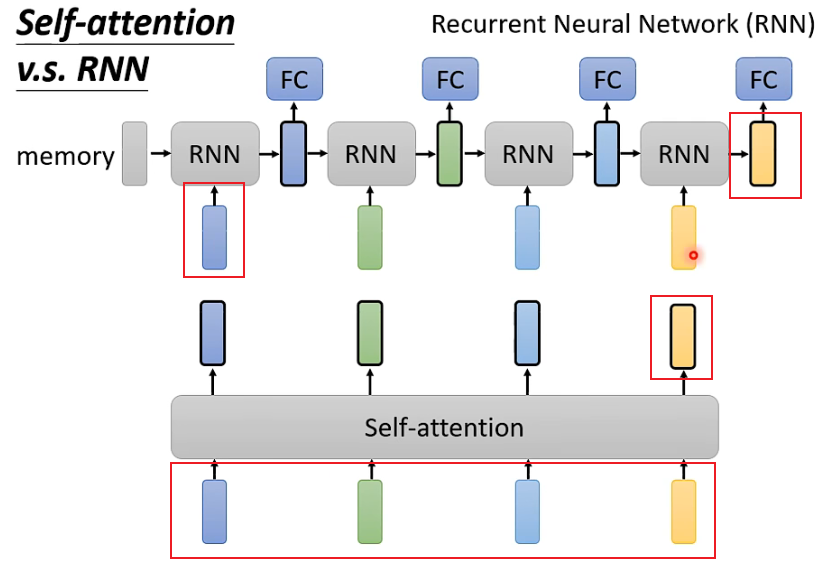
Например, для желтого вывода последнего RNN, если вы хотите включить первый синий вход, вы должны убедиться, что синяя входная информация не теряется при прохождении через каждый слой. Однако, если последовательность очень длинная, это так. сложно гарантировать. Каждый выход Само-внимания напрямую связан со всеми входами.

3. Самовнимание можно рассчитывать параллельно, но между разными слоями РНС существует последовательность.

Ввод внимания к себе вводится одновременно, и вывод также выводится одновременно.