В области глубокого обучения функция активации является ключевым компонентом нейронных сетей, который определяет производительность и производительность сети. В последние годы исследователи предложили множество новых функций активации, среди которых функция активации Swish привлекла большое внимание благодаря своим уникальным преимуществам в производительности. Эта функция была заново открыта в 2017 году и считается вариантом функции Swish. Функция Swish не только обладает превосходной производительностью, но и может эффективно решить проблему исчезновения градиента, поэтому она широко используется в нейронных сетях.

unsetunsetSwish функция активации unsetunset

Математическое определение функции активации Swish выглядит следующим образом:

в,

сигмоидальная функция,

это обучаемый параметр

• когда

Когда эта функция упрощается до

, что эквивалентно сигмовидному линейному блоку (SiLU), впервые предложенному в 2016 году. Позже SiLU была вновь открыта в 2017 году как функция сигмовидной взвешенной линейной единицы (SiL) в обучении с подкреплением. SiLU/SiL была заново открыта более чем через год после того, как она была первоначально открыта как функция Swish, которая изначально предлагалась без каких-либо обучаемых параметров.

,поэтомуβНеявно равно1。Затем,Swish paper обновлена,Предлагаемая функция активации с обучаемым параметром β,Хотя исследователи обычно допускают

,не использует обучаемые параметрыβ。

• для

, функция становится масштабирующей линейной функцией

。

• когда

, сигмовидный компонент имеет тенденцию быть двухточечной функцией 0-1, поэтому функция swish указывает на функцию ReLU. Следовательно, ее можно рассматривать как гладкую функцию, которая нелинейно интерполирует между линейной функцией и функцией ReLU. Эта функция использует немонотонность и, возможно, повлияла на предложение других функций активации с этим свойством, таких как Миш.

Swish — это частный случай функции сжатия сигмоида, когда рассматриваются положительные значения.

2017 год,После анализа набора данных ImageNet,Исследователи из Google обнаружили, что использование функции Swish в качестве функции активации искусственной нейронной сети может улучшить производительность модели по сравнению с ReLU и сигмовидными функциями. Считается, что одной из причин улучшения производительности является то, что функция Swish помогает решить проблему исчезновения градиента во время обратного распространения ошибки.

Преимущества производительности функции Swish в основном отражены в следующих аспектах:

1. Решение проблемы исчезающего градиента：Swishфункция Может создавать большие градиенты во время прямого распространения,полезный Решение проблемы исчезающего градиента,Тем самым улучшая обучение Модельэффективности.
2. немонотонность：Swishфункцияиметьнемонотонность,Это означает, что он может улучшить выразительные способности Модели в определенных диапазонах.,Помогает улучшить производительность модели.
3. Гладкость：Swishфункция Близок к линейному при больших входных значенияхфункция,Это позволяет плавно интерполировать между линейной функцией и функцией ReLU в нейронной сети.,Тем самым улучшая способность обобщения Модели.

Роль функции Swish в обратном распространении ошибки:

В процессе обратного распространения ошибки производная функции Свиша

для

,в

является производной сигмоидальной функции. Эта производная находится в

может сохранять большее значение под влиянием , что помогает повысить эффективность обучения модели.

unsetunsetH-Swish функция активации unsetunset

Hard Swish — это вариант Swish, разработанный для упрощения расчета формул. Исходная формула Swish включает сигмоидальную функцию, которая требует относительно больших вычислительных затрат. Hard Swish заменяет сигмовидную функцию кусочно-линейной функцией, что значительно упрощает вычисления.

В приведенной выше формуле,xактивированфункциявходное значение,иReLU6даRectified Linear Вариант функции Unit (ReLU).

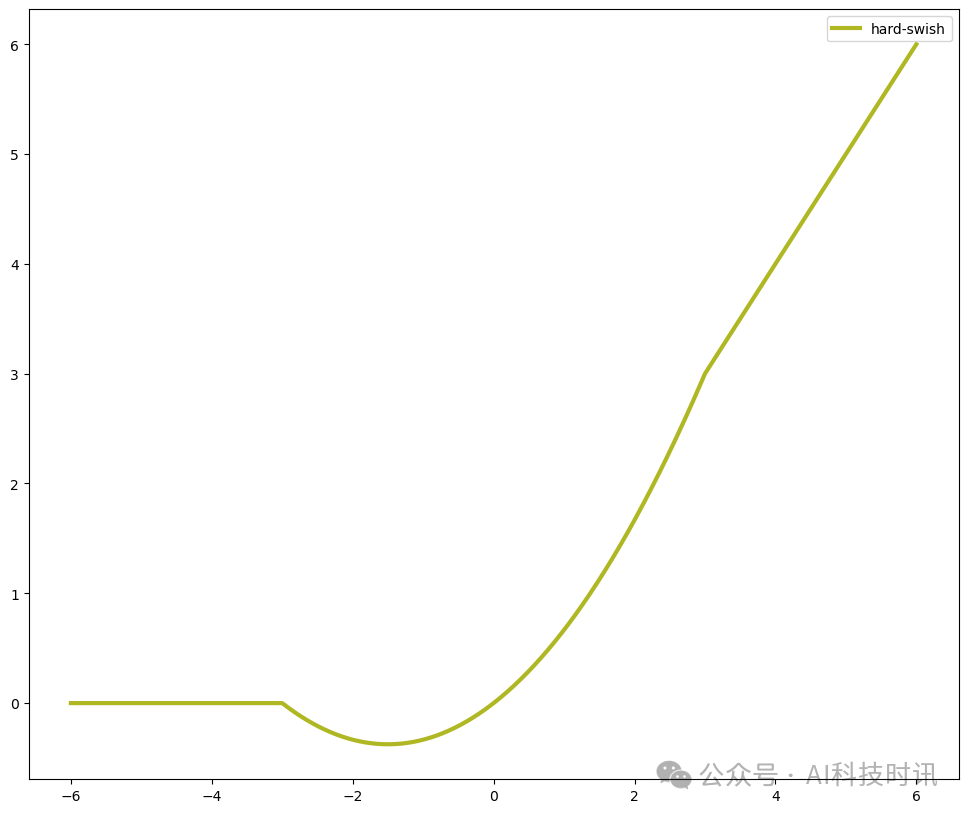
К преимуществам H-Swish перед оригинальным Swish в основном относятся:

1. Вычислительная эффективность：H-SwishИспользуйте кусочно-линейныйфункциязаменилSigmoidфункция,Это существенно упрощает расчеты,Вычислительные затраты сокращаются.
2. Легко интегрировать：H-SwishЛегко интегрировать в существующие приложения машинного обучения,Никаких существенных изменений в архитектуре алгоритма не требуется.,Позволяет разработчикам быстро адаптироваться.
3. производительность поддерживается：хотяH-SwishУпрощает процесс расчета,Но он по-прежнему сохраняет такое же преимущество в производительности, как и оригинальный Swish.,нравиться Решение проблемы исчезающего градиентаинемонотонность。

Благодаря этим преимуществам H-Swish становится оптимизированной функцией активации, особенно в сценариях, требующих эффективных вычислений и быстрого обучения модели.

unsetunset реализует unsetunset

В следующем примере кода библиотека Numpy будет использоваться для реализации Swish, H-Swish и других связанных функций и рисования их графических представлений.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error

# define cost functions
def mish(x):
    return x * np.tanh(np.log(1+np.exp(x)))

def swish(x):
    return (x*np.exp(x))/(np.exp(x)+1)

def relu(x):
    return np.maximum(x,0)

def hard_swish(x, a_max=6, amin=0, add=3, divide=6):
    return x*np.clip(x+add, a_min=amin, a_max=a_max)/divide


# Plot
x = np.linspace(-6, 6, num=1000)
y_mish = mish(x)
y_swish = swish(x)
y_hard_swish = hard_swish(x)
fig,ax = plt.subplots(1, 1, figsize=(12,10))
ax.plot(x, y_mish, label='mish', lw=3,color='#b5002e')
ax.plot(x, y_swish, label='swish', lw=3, color='#001b6e')
ax.plot(x, y_hard_swish, label='hard-swish', lw=3, color='#afb723')
ax.legend()

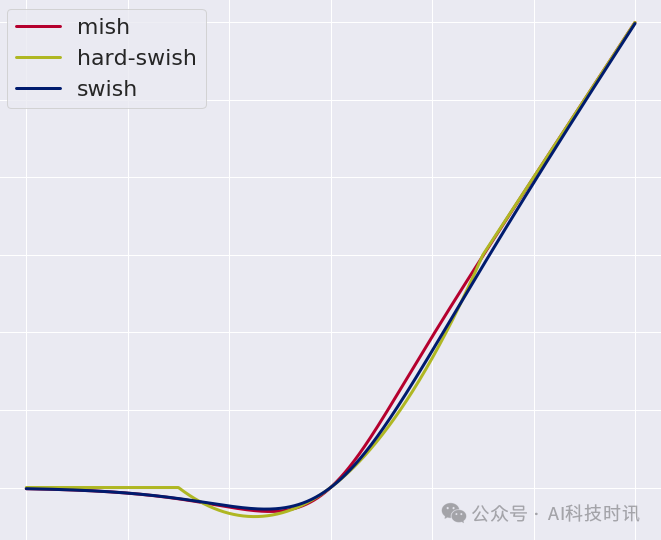
Этот код определяет функции Swish, H-Swish и ReLU6 и использует библиотеку Matplotlib для рисования их графических представлений. Наблюдая за этими графиками, вы можете интуитивно увидеть характеристики этих функций активации, такие как плавность Swish и H-Swish.

unsetunsetsummaryunsetunset

Нельзя игнорировать важность функций активации Swish и H-Swish в области глубокого обучения. Они не только обеспечивают отличную производительность, но и играют ключевую роль в процессе обучения нейронных сетей.

Функция активации Swish привлекла внимание благодаря своей способности эффективно решать проблему исчезновения градиента. Немонотонность и плавность этой функции позволяют ей лучше выражать сложные функциональные отношения при обучении модели, тем самым улучшая способность модели к обобщению. Кроме того, простота и эффективность функции Swish также делают ее широко используемой в практических приложениях.

Функция активации H-Swish является результатом дальнейшей оптимизации на основе Swish. Это значительно повышает эффективность вычислений за счет использования кусочно-линейных функций вместо сигмовидных функций, что ускоряет обучение модели. В то же время H-Swish сохраняет те же преимущества в производительности, что и Swish, что делает его эффективным и действенным выбором функции активации.

В целом применение функций активации Swish и H-Swish в нейронных сетях дает новые идеи и возможности для развития глубокого обучения. Их появление не только обогащает семейство функций активации, но и открывает новые возможности для повышения эффективности и производительности обучения моделей. Поскольку исследования продолжают углубляться, мы можем ожидать, что эти функции активации будут играть более важную роль в будущем и способствовать развитию технологий глубокого обучения.

unsetunsetReferenceunsetunset

• Ramachandran, Prajit; Zoph, Barret; Le, Quoc V. "Searching for Activation Functions"
• Hendrycks, Dan; Gimpel, Kevin. "Gaussian Error Linear Units (GELUs)"
• Elfwing, Stefan; Uchibe, Eiji; Doya, Kenji . "Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning"
• Misra, Diganta (2019). "Mish: A Self Regularized Non-Monotonic Neural Activation Function".
• Atto, Abdourrahmane M.; Pastor, Dominique; Mercier, Gregoire. "Smooth sigmoid wavelet shrinkage for non-parametric estimation"
• Serengil, Sefik Ilkin. "Swish as Neural Networks Activation Function"
• https://serp.ai/hard-swish/