Документ о временных рядах 19|ICML24: хорошая статья об облегченных моделях временных рядов, использующая 1 тыс. параметров для долгосрочного прогнозирования.

Название статьи:SparseTSF: Modeling Long-term Time Series Forecasting with 1k Parameters
Бумажная ссылка:https://arxiv.org/pdf/2402.01533
Ссылка на код:https://github.com/lss-1138/SparseTSF
Предисловие
Недавно я прочитал статью и обнаружил, что облегчение модели в настоящее время является популярным направлением в исследовании временных рядов.
В этом посте предложена бумага SparseTSF,Чрезвычайно легкая модель долгосрочного серийного прогнозирования (LTSF).,Разработан для решения задачи моделирования сложных временных зависимостей в условиях ограниченных вычислительных ресурсов.。Ядро SparseTSF — это технология межпериодного разреженного прогнозирования, которая отделяет периодичность и тенденцию данных временных рядов.,Задачи прогнозирования упрощаются. Конкретно,Этот метод работает за счет понижения разрешения исходной последовательности.,Сосредоточьтесь на прогнозировании межцикловых тенденций,Тем самым эффективно извлекая периодические особенности,Минимизируя при этом сложность и количество параметров Модели. На основе этой технологии,SparseTSFМодель Нет в наличии1000параметры могут быть достигнуты с помощью самых передовых Модель Сопоставимо или даже лучшепроизводительность。также,SparseTSF демонстрирует отличные возможности обобщения.,Это делает его очень подходящим для сценариев с ограниченными вычислительными ресурсами, небольшими выборками или низким качеством.
История исследования
01 Количество параметров и среднеквадратическая ошибка
Хотя более длинные горизонты прогнозирования приносят удобство, они также вносят большую неопределенность. Потому что для этого требуется, чтобы модель могла извлекать более широкие временные зависимости из более длинных исторических окон. Таким образом, моделирование становится более сложным, чтобы уловить эти долгосрочные зависимости от времени. Например, модели на основе Трансформера часто имеют миллионы или даже десятки миллионов параметров, что ограничивает их практическое использование, особенно когда вычислительные ресурсы ограничены.
фактически,Основой точного долгосрочного прогнозирования временных рядов являетсяПрисущая цикличность и тенденции данных。Периодические закономерности можно перевести в динамику между подпоследовательностями.,Тенденции переосмысливаются как особенности внутри подпоследовательностей. Эта декомпозиция открывает новые перспективы для проектирования облегченной модели LTSF.
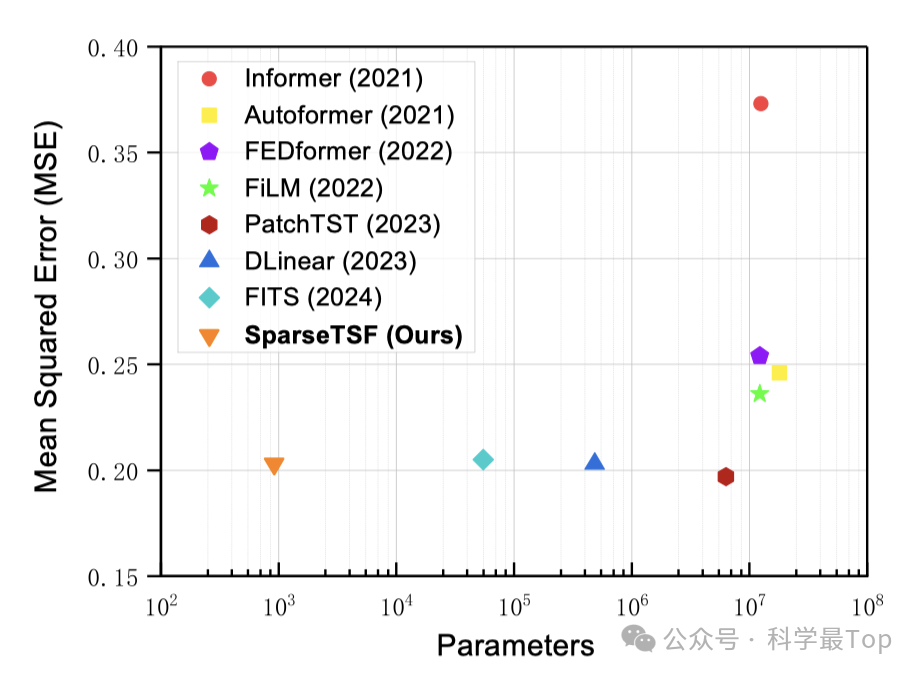
Как показано на рисунке, маленький оранжевый треугольник в левом нижнем углу — это величина параметра и среднеквадратическая ошибка, соответствующие модели в этой статье. Как видно из рисунка, модель в этой статье достигает суммы параметра, пока Среднеквадратическая ошибка в основном соответствует модели Соты. Более чем на 2 порядка меньше.
02 Независимый канал
LTSFМного полейSOTAработа основана наНезависимый канал (CI)метод,Достигайте эффективного прогнозирования путем моделирования долгосрочных зависимостей в одномерных рядах, включая цикличность и тенденции. Конкретно,Метод CI находит общую функцию для каждой одномерной последовательности. Затем предоставьте более целенаправленную и упрощенную модель прогнозирования для каждого канала.,Сокращено сложное рассмотрение взаимоотношений между каналами. DLinear, PatchTST и TiDE используют более сложные структуры на одном канале для извлечения временных зависимостей.,Разработан для достижения превосходной производительности прогнозирования. В этой статье также используется эта стратегия CI.,и сосредоточьтесь на создании более легкого, но эффективного метода фиксации долгосрочных зависимостей в одноканальных временных рядах.
Эта статья работает
Здесь необходимо объяснить основное предположение этой статьи: прогнозируемые данные обычно априори демонстрируют постоянную периодичность.Например,Потребление электроэнергии и транспортный поток обычно имеют фиксированные ежедневные циклы. Как показано на картинке,В этой статье предлагаетсяМежцикловое разреженное предсказание Модель SparseTSF,для улучшения извлечения долгосрочных зависимостей последовательностей,в то же время,Используйте один линейный слой для моделирования задачи LTSF.,Уменьшите размер параметра модели.
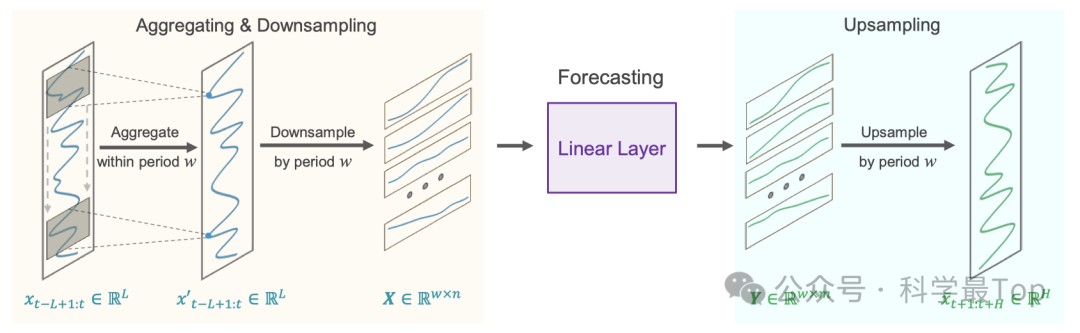
01 Разреженное предсказание между циклами
Предполагая, что временной ряд имеет известную периодичность, первым шагом является уменьшение исходной последовательности на w подпоследовательностей. Затем к этим подпоследовательностям применяется модель с общими параметрами для прогнозирования. После завершения прогнозирования подпоследовательность подвергается повышающей дискретизации обратно до полной последовательности прогнозирования.
Интуитивно этот процесс прогнозирования выглядит как скользящий прогноз с разреженным интервалом w, выполняемый полностью связным слоем, который разделяет параметры в течение фиксированного периода w. Думайте об этом как о модели, делающей редкие скользящие прогнозы между периодами.
Технически говоря, процесс понижающей дискретизации эквивалентен преобразованию последовательности в матрицу размера n × w, а затем преобразованию ее в матрицу размера w × n. Разреженное скользящее предсказание эквивалентно применению линейного слоя размера n×m к последнему измерению матрицы, в результате чего получается матрица w×m. Шаг повышения дискретизации эквивалентен транспонированию и изменению формы матрицы w × m обратно в полную последовательность прогнозирования длины H.
Однако в настоящее время этот метод по-прежнему сталкивается с двумя проблемами: (i) потеря информации, поскольку для прогнозирования используется только одна точка данных в каждом периоде, а остальные точки данных игнорируются (ii) усиление влияния выбросов из-за понижения выборки; Экстремальные значения, существующие в подпоследовательности, могут напрямую влиять на результаты прогнозирования.
Чтобы решить эти проблемы, автор этой статьи выполняет скользящую агрегацию исходной последовательности перед выполнением разреженного прогнозирования, как показано на рисунке 2. Каждая агрегированная точка данных содержит информацию о других точках в окружающем ее периоде, что решает проблему (i). Более того, поскольку совокупное значение по сути представляет собой средневзвешенное значение окружающих точек, оно смягчает влияние выбросов, тем самым решая проблему (ii). Технически такая скользящая агрегация может быть достигнута с использованием заполнения нулями и одномерной свертки с размером ядра 2×⌊w/2⌋+1.
02 Нормализация экземпляра и функция потерь
В этой статье используется стратегия нормализации экземпляров, позволяющая вычитать среднее значение последовательности перед входом в модель и добавлять его обратно после вывода модели.
Функция потерь использует классическую среднеквадратическую ошибку (MSE) в качестве функции потерь SparseTSF. Эффективность прогнозирования модели измеряется путем расчета квадрата ошибки между прогнозируемым значением и истинным значением.
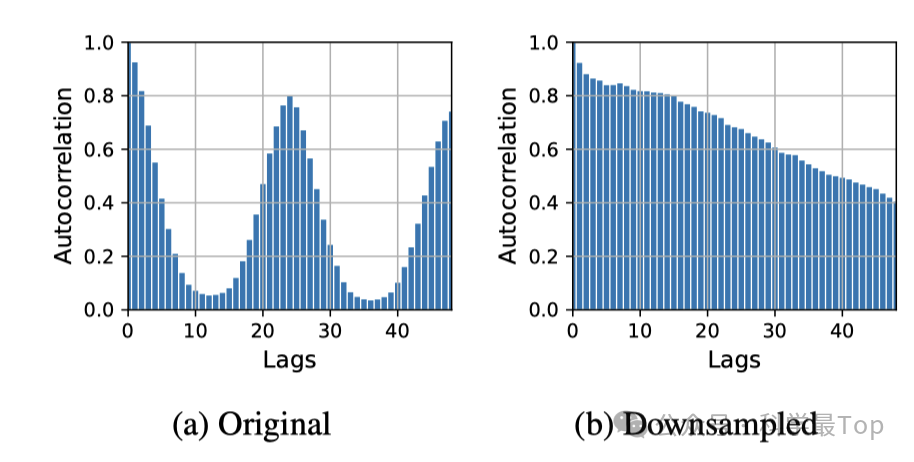
Кроме того, еще одна важная работа этой статьи представляет собой теоретический анализ модели SparseTSF с упором на эффективность ее параметров и эффективность разреженной технологии.
Эксперименты и выводы
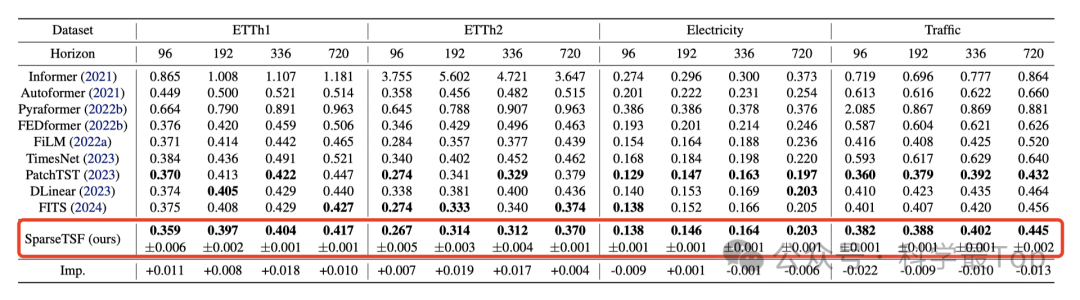
Недостатки этой статьи:
SparseTSF достигает производительности, которая конкурирует с современными моделями или даже превосходит их при чрезвычайно малом масштабе параметров, что делает его сильным кандидатом в средах с ограниченными вычислительными ресурсами и легковесной моделью в области долгосрочного прогнозирования рядов. . Достигнута еще одна веха.
SparseTSFМодель ОбработкаСверхдлинные циклы, множественные циклы и ситуации, когда циклы неочевидны.,могут возникнуть трудности,Потому что разреженные методы могут только уменьшать дискретизацию и разлагать один основной период. В будущем мы можем рассмотреть решение проблемы извлечения признаков из сверхдлинных и многопериодных данных.,Стремитесь достичь наилучшего баланса между Модельпроизводительностью и масштабом параметров.

Неразрушающее увеличение изображений одним щелчком мыши, чтобы сделать их более четкими артефактами искусственного интеллекта, включая руководства по установке и использованию.

Копикодер: этот инструмент отлично работает с Cursor, Bolt и V0! Предоставьте более качественные подсказки для разработки интерфейса (создание навигационного веб-сайта с использованием искусственного интеллекта).

Новый бесплатный RooCline превосходит Cline v3.1? ! Быстрее, умнее и лучше вилка Cline! (Независимое программирование AI, порог 0)

Разработав более 10 проектов с помощью Cursor, я собрал 10 примеров и 60 подсказок.

Я потратил 72 часа на изучение курсорных агентов, и вот неоспоримые факты, которыми я должен поделиться!
Идеальная интеграция Cursor и DeepSeek API

DeepSeek V3 снижает затраты на обучение больших моделей

Артефакт, увеличивающий количество очков: на основе улучшения характеристик препятствия малым целям Yolov8 (SEAM, MultiSEAM).

DeepSeek V3 раскручивался уже три дня. Сегодня я попробовал самопровозглашенную модель «ChatGPT».

Open Devin — инженер-программист искусственного интеллекта с открытым исходным кодом, который меньше программирует и больше создает.

Эксклюзивное оригинальное улучшение YOLOv8: собственная разработка SPPF | SPPF сочетается с воспринимаемой большой сверткой ядра UniRepLK, а свертка с большим ядром + без расширения улучшает восприимчивое поле

Популярное и подробное объяснение DeepSeek-V3: от его появления до преимуществ и сравнения с GPT-4o.

9 основных словесных инструкций по доработке академических работ с помощью ChatGPT, эффективных и практичных, которые стоит собрать

Вызовите deepseek в vscode для реализации программирования с помощью искусственного интеллекта.

Познакомьтесь с принципами сверточных нейронных сетей (CNN) в одной статье (суперподробно)

50,3 тыс. звезд! Immich: автономное решение для резервного копирования фотографий и видео, которое экономит деньги и избавляет от беспокойства.

Cloud Native|Практика: установка Dashbaord для K8s, графика неплохая

Краткий обзор статьи — использование синтетических данных при обучении больших моделей и оптимизации производительности

MiniPerplx: новая поисковая система искусственного интеллекта с открытым исходным кодом, спонсируемая xAI и Vercel.

Конструкция сервиса Synology Drive сочетает проникновение в интрасеть и синхронизацию папок заметок Obsidian в облаке.

Центр конфигурации————Накос

Начинаем с нуля при разработке в облаке Copilot: начать разработку с минимальным использованием кода стало проще

[Серия Docker] Docker создает мультиплатформенные образы: практика архитектуры Arm64

Обновление новых возможностей coze | Я использовал coze для создания апплета помощника по исправлению домашних заданий по математике

Советы по развертыванию Nginx: практическое создание статических веб-сайтов на облачных серверах

Feiniu fnos использует Docker для развертывания личного блокнота Notepad

Сверточная нейронная сеть VGG реализует классификацию изображений Cifar10 — практический опыт Pytorch

Начало работы с EdgeonePages — новым недорогим решением для хостинга веб-сайтов

[Зона легкого облачного игрового сервера] Управление игровыми архивами


