Основной метод тестирования пути основан на графе потока управления программой путем анализа сложности цикла структуры управления и получения базового набора исполняемых путей для разработки тестовых примеров. Разработанные тестовые примеры должны гарантировать бесперебойную работу программы во время теста. Покрытие операторов — 100%, покрытие условий — 100%.

На основе графа потока управления программой путем анализа сложности цикла структуры управления выводится базовый набор путей к исполняемым файлам для разработки тестовых примеров.

Включает следующие 4 шага и метод инструмента:

• Схема потока управления программой: графический метод описания потока управления программой.
• программа Цикломатическая сложность: мера сложности Маккейба. Количество независимых путей в базовом пути сбора можно получить из цикломатической сложности программы, которая является верхней границей количества тестовых вариантов использования, которые должны быть выполнены хотя бы один раз для каждого исполняемого оператора в программе.
• Вариант использования экспорта: ввод данных сценария использования теста и ожидаемые результаты на основе цикломатической сложности и структуры программы.
• Подготовьте варианты использования для тестирования: обеспечьте выполнение каждого пути в базовом наборе путей.

1. Схема управления программой: графический метод описания потока управления программой.

Круг называется узлом графа потока управления и представляет один или несколько операторов без ветвей или операторов исходной программы.

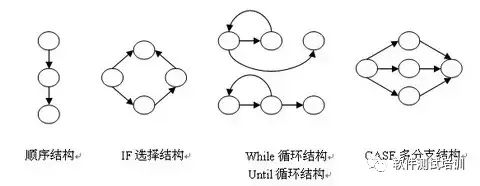
• Каждый круг в графе называется узлом потокового графа и представляет одно или несколько операторов.
• Стрелки в графе потока называются ребрами или соединениями и представляют поток управления.
• Любой проект процесса должен быть преобразован в граф потока управления.

Как нарисовать блок-схему управления на основе блок-схемы программы?

• В селективной или многоветвевой структуре должен быть узел конвергенции, в котором сходятся ветви.
• Диапазон, ограниченный ребрами и узлами, называется регионом. При подсчете регионов область за пределами графа также следует записывать как регион.

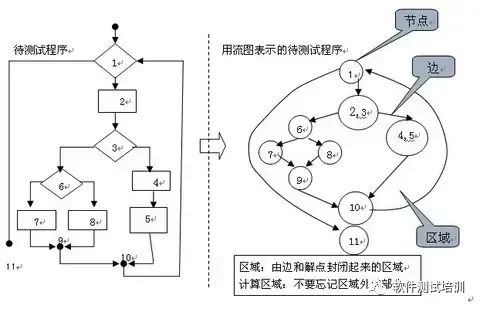
• Независимый путь: путь, который движется хотя бы по одному новому ребру.

2. Этапы базового метода тестирования пути

1. Нарисуйте схему потока управления

Блок-схему можно сопоставить с соответствующей блок-схемой (при условии, что ромбовидное поле решения блок-схемы не содержит сложных условий). В потоковом графе каждый круг, называемый узлом потокового графа, представляет одно или несколько операторов. Последовательность блоков обработки и окно принятия решений в форме ромба могут быть сопоставлены с узлом. Стрелки на графе потока, называемые ребрами или соединениями, представляют поток управления, аналогично стрелкам на графе потока. Ребро должно заканчиваться в узле, даже если узел не представляет никакого оператора (например: структура if-else-then). Диапазон, ограниченный ребрами и узлами, называется регионом. Диапазон за пределами графика следует учитывать при расчете площади.

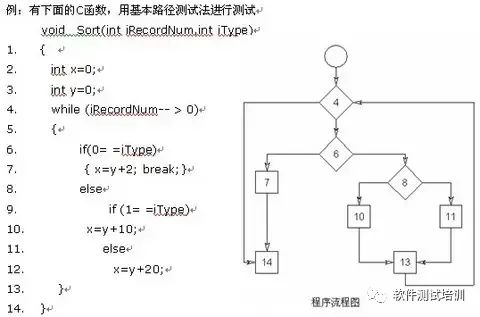
Нарисуйте блок-схему программы и соответствующую блок-схему управления следующим образом.

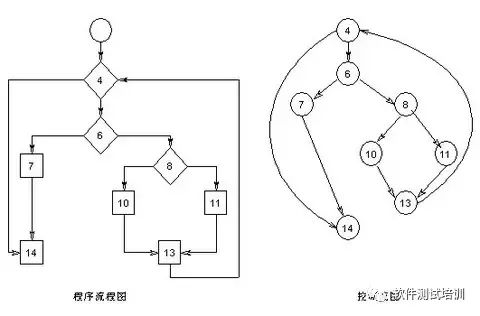
2. Вычислить цикломатическую сложность

Цикломатическая сложность — это программная метрика, которая обеспечивает количественную меру логической сложности программы. Эта метрика используется для расчета количества основных независимых путей программы и является верхней границей количества тестов, гарантирующих, что все операторы являются верными. выполнен хотя бы один раз. Независимый путь должен содержать ребро, которое не использовалось до определения.

Существует три способа расчета цикломатической сложности:

• Количество регионов в графе потока соответствует сложности типа кольца;
• Учитывая цикломатическую сложность V(G) графа потока G, она определяется как V(G)=E-N+2, E — количество ребер в графе потока, а N — количество узлов в потоке. график;
• Учитывая цикломатическую сложность V(G) потокового графа G, она определяется как V(G)=P+1, где P — количество узлов принятия решений в потоковом графе G.

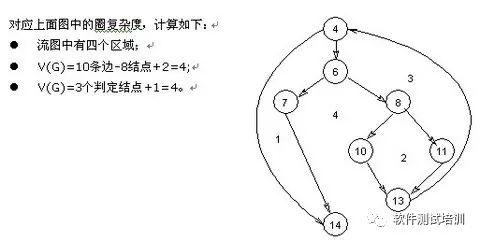
3. Экспорт тестовых примеров

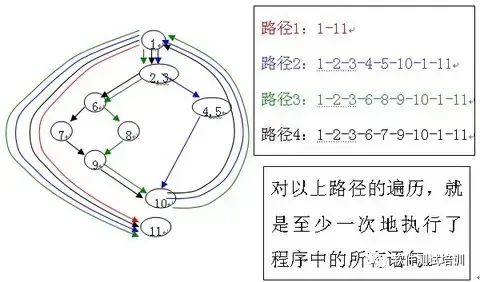
Согласно описанному выше методу расчета можно получить четыре независимых пути. (Независимый путь относится к пути программы, который вводит хотя бы один новый оператор обработки или новое решение по сравнению с другими независимыми путями. Значение V(G) точно равно количеству независимых путей в программе.)

Путь 1:4-14

Путь 2: 4-6-7-14

Путь 3: 4-6-8-10-13-4-14

Путь 4: 4-6-8-11-13-4-14

В соответствии с указанными выше независимыми путями спроектируйте входные данные так, чтобы программа выполняла указанные выше четыре пути соответственно.

4. Подготовьте тестовые примеры

Чтобы гарантировать выполнение каждого пути в наборе базовых путей, в соответствии с условиями, заданными узлом оценки, выберите соответствующие данные, чтобы гарантировать возможность тестирования определенного пути. Тестовые случаи, которые удовлетворяют базовому набору путей, указанному выше. пример:

3. Дело

В следующем примере блок-схемы программы описывается ввод до 50 значений (с –1 в качестве конечного флага ввода) и расчет количества, общего количества баллов и среднего значения действительных оценок учащихся.

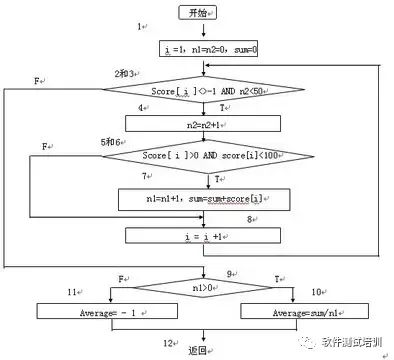
1. Блок-схема процесса экспорта

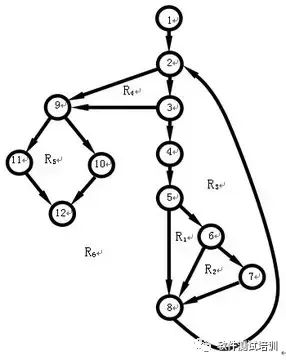
3. Определить циклическую метрику сложности V(G):

1)V(G)= 6 (площадей)

　　2)V(G)=E–N+2=16–12+2=6

Где E — количество ребер в графе потока, а N — количество узлов;

　　3)V(G)=P+1=5+1=6

Где P — количество узлов предиката. В потоковом графе узлы 2, 3, 5, 6 и 9 являются узлами-предикатами.

Шаг 3. Определите базовый набор путей (то есть набор независимых путей). Таким образом, можно определить 6 независимых путей:

Путь 1: 1-2-9-10-12

Путь 2: 1-2-9-11-12

Путь 3: 1-2-3-9-10-12

Путь 4: 1-2-3-4-5-8-2…

Путь 5: 1-2-3-4-5-6-8-2…

Путь 6: 1-2-3-4-5-6-7-8-2…

4. Разработайте набор тестовых примеров для каждого независимого пути, чтобы заставить программу выполниться хотя бы один раз на этом пути.

1) Тестовый пример для пути 1 (1-2-9-10-12):

　　счет[k]=действительное значение оценки, когда k < i ;

　　score[i]=–1, 2≤i≤50;

Ожидаемый результат: подсчитайте правильное количество баллов n1, общую сумму баллов и средний балл на основе введенных действительных баллов.

​2) Тестовый пример для пути 2 (1-2-9-11-12):

　　score[ 1 ]= – 1 ;

Желаемый результат: среднее значение = – 1, остальные величины остаются в исходных значениях.

3) Тестовые примеры для пути 3 (1-2-3-9-10-12):

Ввод более 50 действительных результатов означает попытку обработать 51 результат, причем первые 51 должны быть действительными;

Ожидаемые результаты: n1=50. Подсчитайте правильный общий балл и средний балл.

4) Тестовые примеры для пути 4 (1-2-3-4-5-8-2...):

счет[i]=действительный балл,когдаi<50;

　　score[k]<0, k< i ;

Ожидаемый результат: подсчитайте правильное количество баллов n1, общую сумму баллов и средний балл на основе введенных действительных баллов.