Технология Locality Sensitive Hash (LSH) является ключевым методом быстрого приближенного поиска ближайшего соседа (ANN) и широко используется для достижения эффективного и точного поиска по сходству. Эта технология является неотъемлемой частью многих крупнейших технологических компаний мира, включая Google, Netflix, Amazon, Spotify и Uber.

АмазонкаАнализируя общение пользователя с пользователемсходство,Рекомендуйте пользователям новые продукты на основе истории покупок.。Googleвыполнено пользователемпоискчас,на самом деле выполняет сходствопоиск,Оцениватьпоиск Слова иGoogleСходство индексированного интернет-контента。иSpotifyПричина, по которой мы можем рекомендовать музыку, которая соответствует вкусам пользователей,потому что он успешно сопоставляет пользователей с другими пользователями со схожими вкусами посредством сходствапоискалгоритм.

Преимущество технологии LSH заключается в том, что она может обеспечить высококачественные результаты поиска, сохраняя при этом скорость поиска. Это критически важно для обработки крупномасштабных наборов данных и обеспечения возможностей поиска в реальном времени. В этой статье мы углубимся в теоретическую основу алгоритма LSH и предоставим простой для понимания пример реализации Python, который поможет читателям лучше освоить эту технологию.

Сложность поиска

При работе с наборами данных, содержащими миллионы или даже миллиарды данных, эффективное выполнение межвыборочных сравнений становится огромной проблемой.

Попытка сравнить все пары образцов одну за другой непрактична даже на самом современном оборудовании. Временная сложность этого метода равна , что означает, что по мере увеличения объема данных требуемые время и ресурсы будут увеличиваться в квадрате. Сложность даже сравнения одного запроса с миллиардами выборок налагает огромную вычислительную нагрузку на большие наборы данных.

Более того, каждая выборка обычно хранится в виде многомерного вектора, что еще больше усложняет вычисления. Вычисление подобия в многомерном пространстве не только затратно, но и неэффективно.

Столкнувшись с этими проблемами, возникает естественный вопрос: существует ли метод, который может обеспечить поиск сублинейной сложности, то есть время поиска не увеличивается линейно с объемом данных? Ответ: да.

Ключом к решению этой проблемы является принятие приближенной стратегии поиска. Вместо того, чтобы выполнять исчерпывающее сравнение каждого вектора, вы можете сузить поиск путем аппроксимации только тех векторов, которые, скорее всего, будут релевантными.

Алгоритм локально-чувствительного хеширования (LSH) — один из таких методов, который может обеспечить сублинейное время поиска. Он быстро идентифицирует потенциальных ближайших соседей, сопоставляя похожие элементы с одним и тем же местоположением «корзины» или «хеш-таблицы». В этой статье будет подробно описан алгоритм LSH и подробно обсуждены лежащие в его основе принципы работы.

Хэширование с учетом местоположения

Столкнувшись с вычислительной сложностью поиска пар подобных векторов, требуемый объем вычислений может стать невыполнимым даже для небольших наборов данных.

Рассмотрим сценарий индексации векторов. Если вы хотите найти ближайшее совпадение для нового вектора, вам необходимо сравнить его со всеми другими векторами в базе данных. Временная сложность этого подхода линейна, что для больших наборов данных означает, что поиск не может быть завершен быстро.

В идеале мы хотим сравнивать только те векторы, которые могут совпадать, то есть потенциальные пары-кандидаты. Чтобы уменьшить количество необходимых сравнений, был создан алгоритм локально-чувствительного хеширования (LSH). LSH — это метод, который отображает похожие элементы в одну и ту же хэш-корзину. Он включает в себя множество различных методов, и в этой статье будет представлен традиционный метод, который включает в себя следующие шаги:

• Шардинг документа (шинлинг)：Разделить документ на сегменты。
• MinHashing：один для оценкисобиратьвероятность сходстваалгоритм。
• Функция Banded LSH (Banding)：финальныйLSHфункция,Используется для разделения и хеширования векторов.

Суть алгоритма LSH заключается в том, что, когда хотя бы одна операция хэширования приводит к сопоставлению двух векторов с одним и тем же значением, эти два вектора считаются парой-кандидатом, то есть возможным совпадением.

Этот процесс аналогичен процессу хеширования в словарях Python, где ключи обрабатываются с помощью хэш-функции и сопоставляются с определенным сегментом, а затем соответствующее значение связывается с этим блоком.

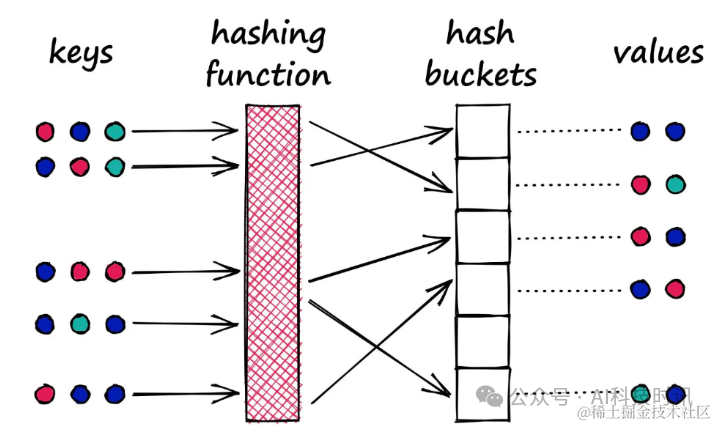
«Типичная хэш-функция：предназначен для преобразования различных значений（независимо от того, насколько похожи）разложить по разным ведрам

Однако существует важное различие между хэш-функциями, используемыми в LSH, и хеш-функциями в традиционных словарях:

В словаре цель состоит в том, чтобы свести к минимуму возникновение нескольких сопоставлений ключей с одним и тем же сегментом, чтобы уменьшить конфликты. Философия LSH прямо противоположна. Она надеется максимизировать конфликты, но в идеале этот конфликт возникает только при одинаковых входных данных.

«Хеш-функция LSH：Цель — поместить схожие значения в одно ведро.

Методы хеширования в LSH не уникальны. Хотя все они следуют основной логике помещения одинаковых выборок в одну и ту же корзину с помощью хэш-функции, они могут сильно различаться в своей конкретной реализации. Традиционный метод, представленный в этой статье, включает этапы шардинга документа (шинлинга), минхэшинга и бандинга (бэндинга).

Shingling, MinHashing, LSH

Метод локально-чувствительного хэширования (LSH) охватывает три ключевых шага для эффективной идентификации похожих элементов в крупномасштабных наборах данных.

• Сначала преобразуйте текст в разреженные векторы, используя k-shingling.
• Затем создайте «подпись» через MinHashing.
• Наконец, процесс LSH используется для отсеивания пар кандидатов.

В этой статье будет подробно описан этот процесс

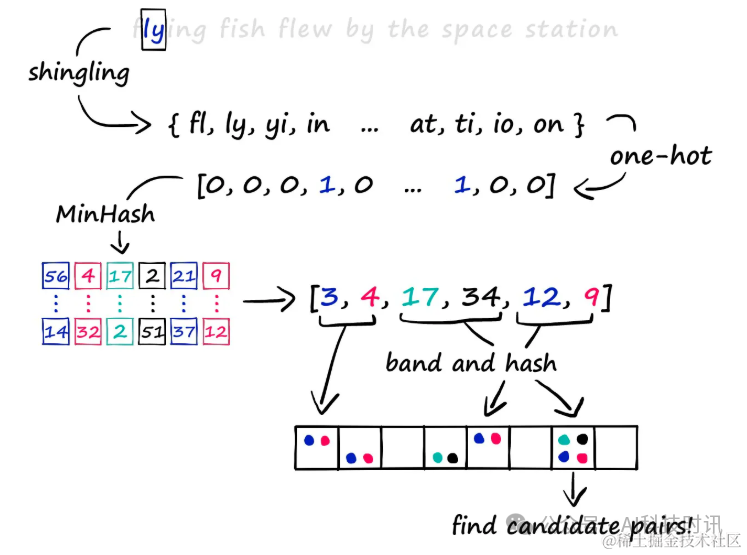
k-Shingling: преобразование текста в черепицу

k-Shingling Это метод преобразования текстовой строки в набор «черепиц» (сегментов). Этот процесс аналогичен наведению окна длиной k на текст и записи содержимого окна на каждом этапе. Таким способом можно получить коллекцию фрагментов текста.

В Python вы можете создать простую функцию k-шинлинга следующим образом:

a = "flying fish flew by the space station"
b = "we will not allow you to bring your pet armadillo along"
c = "he figured a few sticks of dynamite were easier than a fishing pole to catch fish"

def shingle(text: str, k: int=2):
    shingle_set = []
    for i in range(len(text) - k+1):
        shingle_set.append(text[i:i+k])
    return set(shingle_set)

a = shingle(a, k)
b = shingle(b, k)
c = shingle(c, k)
print(a)

# {'y ', 'pa', 'ng', 'yi', 'st', 'sp', 'ew', 'ce', 'th', 'sh', 'fe', 'e ', 'ta', 'fl', ' b', 'in', 'w ', ' s', ' t', 'he', ' f', 'ti', 'fi', 'is', 'on', 'ly', 'g ', 'at', 'by', 'h ', 'ac', 'io'}

Чтобы создать разреженные векторы после наличия черепицы, все наборы необходимо объединить в один большой словарь наборов (или словарь), который содержит все черепицы во всех наборах.

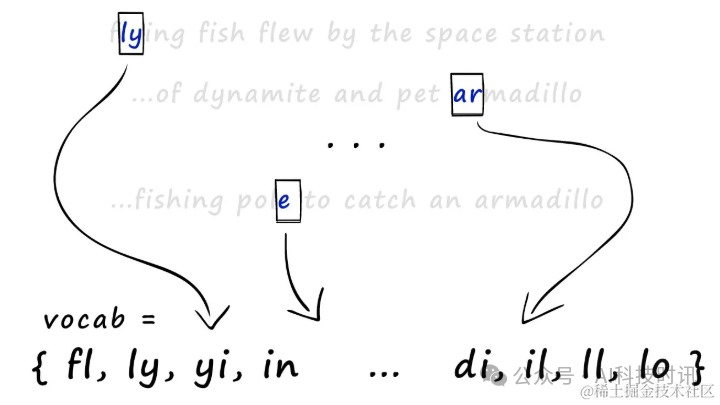
Все наборы черепицы объединяются для создания словаря (vocab).

Используя этот словарь, создайте разреженные векторы для каждого набора. В частности, создайте вектор из всех нулей по всей длине словаря, затем проверьте, какие черепицы появляются в наборе, и установите значение соответствующей позиции на 1.

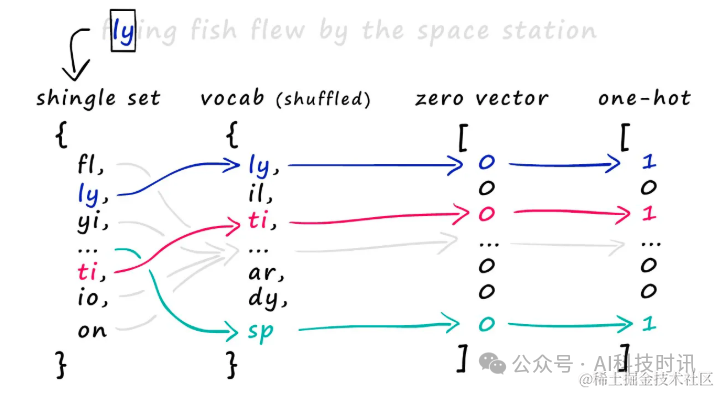
Чтобы создать горячее кодирование, один набор шинглов сопоставляется со словарем, чтобы определить, где следует поместить 1 в векторе нулей. Для каждого появления черепицы найдите его позицию в словаре и установите для соответствующей позиции нулевого вектора значение 1. Вот как работает горячее кодирование.

Minhashing

Подписи MinHashing создаются путем преобразования разреженных векторов в плотные числовые векторы. Этот процесс включает в себя следующие ключевые этапы:

1. Сгенерируйте случайно переставленные векторы счета：первый,Создайте вектор отсчетов от 1 до длины словаря.,и расположите их случайным образом. Этот упорядоченный вектор будет использоваться в последующих вычислениях MinHashing.
2. Выровнять 1 в разреженном векторе：затем,Для каждой единицы в разреженном векторе,Нужно найти наименьшее число перестановки, которое ему соответствует. Это число будет использоваться в качестве значения в подписи.

Проиллюстрируем этот процесс на конкретном примере:

• Предполагая, что словарь меньшего размера (6 значений), это помогает визуализировать процесс MinHashing.
• Случайным образом расположите векторы счета из словаря,Например：[5, 1, 3, 2, 4, 6]。
• Затем каждая позиция в разреженном векторе проверяется, существует ли соответствующая шингл. Если он существует, соответствующее значение разреженного вектора равно 1, если оно не существует, оно равно 0;

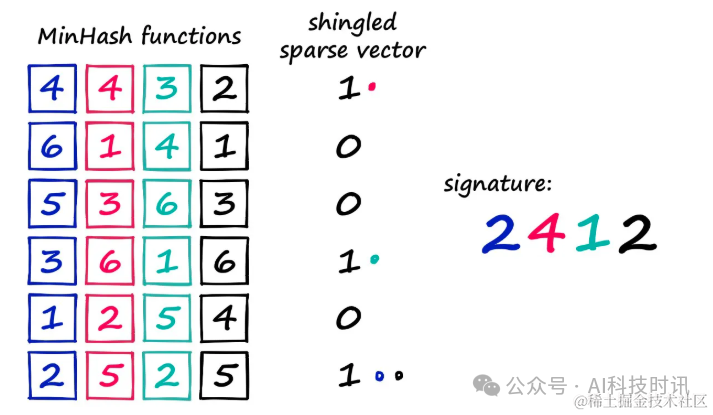
Здесь четыре минхеш-функции/вектора используются для создания четырехзначного вектора подписи. Если вы начнете считать с 1 в каждой минхеш-функции и найдете первое значение, которое совпадает с 1 в разреженном векторе, вы получите 2412. Таким образом, значение MinHash может быть сгенерировано для каждой единицы в разреженном векторе. Чтобы создать полную подпись MinHash, вам необходимо назначить разные функции MinHash для каждой позиции в подписи и повторить описанный выше процесс несколько раз. Реализуйте это ниже с помощью кода. Есть три шага:

1. Сгенерируйте рандомизированный вектор минхеша

vocab = a.union(b).union(c)
hash_ex = list(range(1, len(vocab)+1))

from random import shuffle

shuffle(hash_ex)

1. Выполните итерацию по этому случайному вектору MinHash (начиная с 1), сопоставляя индекс каждого значения с эквивалентным значением в разреженном векторе a_1hot. Если найдено 1, этот индекс является значением со знаком.

a_1hot = [1 if i in a else 0 for i in vocab]
b_1hot = [1 if i in b else 0 for i in vocab]
c_1hot = [1 if i in c else 0 for i in vocab]
print(f"7 -> {hash_ex.index(7)}")

for i in range(1, 5):
    print(f"{i} -> {hash_ex.index(i)}")
    
for i in range(1, len(vocab)+1):
    idx = hash_ex.index(i)
    signature_val = a_1hot[idx]
    print(f"{i} -> {idx} -> {signature_val}")
    if signature_val == 1:
        print('match!')
        break

1 -> 58 -> 0
2 -> 19 -> 0
3 -> 96 -> 0
4 -> 92 -> 0
5 -> 83 -> 0
6 -> 98 -> 1
match!

1. Создайте подпись за несколько итераций

def create_hash_func(size: int):
    # Создать хэш-вектор/функцию
    hash_ex = list(range(1, len(vocab)+1))
    shuffle(hash_ex)
    return hash_ex

def build_minhash_func(vocab_size: int, nbits: int):
    # Создайте несколько векторов минхеша
    hashes = []
    for _ in range(nbits):
        hashes.append(create_hash_func(vocab_size))
    return hashes

# Создайте 20 векторов минхеша.
minhash_func = build_minhash_func(len(vocab), 20)

def create_hash(vector: list):
    # Функции, используемые для создания подписей
    signature = []
    for func in minhash_func:
        for i in range(1, len(vocab)+1):
            idx = func.index(i)
            signature_val = vector[idx]
            if signature_val == 1:
                signature.append(idx)
                break
    return signature

# Создать подпись
b_1hot = [1 if i in b else 0 for i in vocab]
c_1hot = [1 if i in c else 0 for i in vocab]

a_sig = create_hash(a_1hot)
b_sig = create_hash(b_1hot)
c_sig = create_hash(c_1hot)

print(a_sig)
print(b_sig)
# [70, 19, 84, 88, 112, 46, 54, 75, 68, 15, 15, 85, 94, 93, 51, 29, 75, 68, 110, 108]
# [62, 14, 106, 80, 57, 114, 62, 12, 127, 39, 121, 104, 14, 23, 2, 127, 12, 33, 45, 45]

Принцип MinHashing не сложен. С помощью описанных выше шагов разреженный вектор был сжат в плотную подпись, содержащую 20 чисел.

Перенос информации из разреженных векторов в сигнатуры

Ключевой вопрос заключается в том, сохраняется ли достаточно информации для эффективного сравнения сходства при преобразовании исходного разреженного вектора в подпись MinHash. Чтобы убедиться в этом, мы можем вычислить сходство Жаккара между исходным вектором и вектором сигнатуры. Сходство Жаккара — это мера сходства между двумя множествами путем сравнения размера их пересечения и объединения. Сходство Жаккара можно сначала вычислить с использованием исходного набора шинглов, а затем тот же расчет выполнить для соответствующей подписи MinHash.

def jaccard(a: set, b: set):
    return len(a.intersection(b)) / len(a.union(b))

print(jaccard(a, b), jaccard(set(a_sig), set(b_sig)))
# 0.02531645569620253, 0.0

print(jaccard(a, c), jaccard(set(a_sig), set(c_sig)))
# 0.10309278350515463, 0.030303030303030304

print(jaccard(b, c), jaccard(set(b_sig), set(c_sig)))
# 0.043478260869565216, 0.03225806451612903

Сравнивая исходную сборку шингла и подпись MinHash, собираем Jaccardсходство.,Может Оцениватьинформациясуществовать Степень сохранения при конвертации。Если сходство набора подписей близко к сходству исходного набора, это указывает на то, что подпись MinHash эффективно сохраняет информацию о сходстве в исходном разреженном векторе.

Чередование и хеширование

На заключительном этапе локально-зависимого хеширования (LSH) для обработки вектора подписи используется метод чередования. Этот метод делит подпись на несколько фрагментов и хэширует каждый фрагмент для поиска коллизий хэшей.

Группирование решает проблемы, которые могут возникнуть при прямом хешировании всего вектора, путем разделения вектора на части, называемые «полосами». Этот подход позволяет идентифицировать совпадающие подвекторы между векторами, даже если все векторы не идентичны.

Непосредственное хеширование целых векторов может затруднить создание хеш-функции, которая точно идентифицирует их сходство. Весь вектор не обязательно должен быть равным, похожими должны быть только его части. Разделение полос обеспечивает гибкое условие: всякий раз, когда любые два подвектора сталкиваются, соответствующие полные векторы считаются парами-кандидатами.

Как работает зонирование

Метод полосы решает эту проблему, разбивая вектор на части, называемые полосами (b), а затем пропуская каждый подвектор через хэш-функцию.

Предположим, что 100-мерный вектор разделен на 20 полос, что дает 20 возможностей определить совпадающие подвекторы между векторами. Каждый субвектор обрабатывается с помощью хеш-функции и отображается в хэш-ведро.

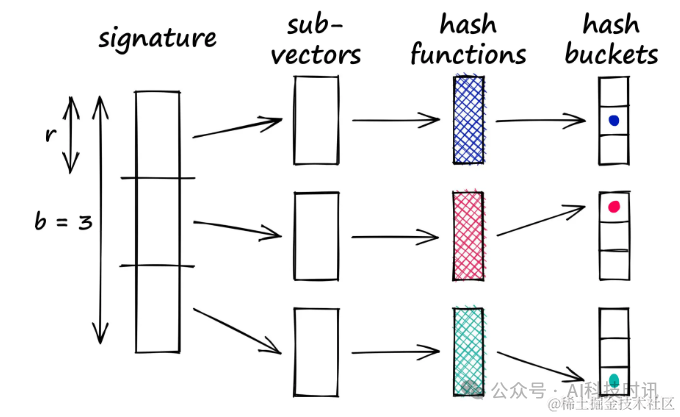
Подпись разбивается на b субвекторов, каждый субвектор обрабатывается с помощью хэш-функции и отображается в хэш-корзину, и всякий раз, когда любые два субвектора сталкиваются, соответствующий полный вектор рассматривается как пара-кандидат.

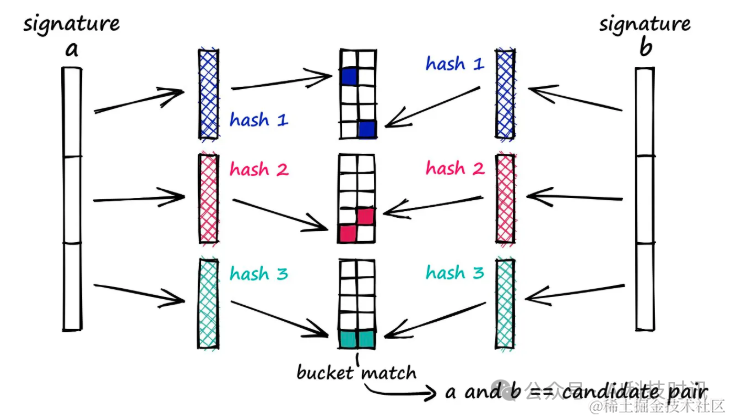
Эквивалентные субвекторы во всех сигнатурах должны обрабатываться одной и той же хеш-функцией, и для всех субвекторов может использоваться одна хэш-функция.

Простая версия может быть реализована на Python. Во-первых, начните с разделения векторов сигнатур a, b и c:

def split_vector(signature, b):
    assert len(signature) % b == 0
    r = int(len(signature) / b)
    # code splitting signature in b parts
    subvecs = []
    for i in range(0, len(signature), r):
        subvecs.append(signature[i : i+r])
    return subvecs

band_a = split_vector(a_sig, 10)
band_b = split_vector(b_sig, 10)
band_c = split_vector(c_sig, 10)
print(band_c)

[[30, 60],
 [84, 125],
 [135, 90],
 [130, 107],
 [76, 16],
 [44, 119],
 [109, 135],
 [30, 76],
 [95, 33],
 [41, 32]]

Затем он просматривает список, чтобы определить совпадения между подвекторами. Если совпадение найдено, эти векторы используются в качестве пар-кандидатов.

for b_rows, c_rows in zip(band_b, band_c):
    if b_rows == c_rows:
        print(f"Candidate pair: {b_rows} == {c_rows}")
        break
        
for a_rows, b_rows in zip(band_a, band_b):
    if a_rows == b_rows:
        print(f"Candidate pair: {a_rows} == {b_rows}")
        break
        
for a_rows, c_rows in zip(band_a, band_c):
    if a_rows == c_rows:
        print(f"Candidate pair: {b_rows} == {c_rows}")
        break

Тест ЛШ

Реализация в ее нынешнем виде очень неэффективна. Если вы хотите реализовать LSH, вам следует использовать библиотеку, предназначенную для поиска по сходству, например Faiss.

Тем не менее, как работает LSH, становится понятнее, если посмотреть на то, как написан код. Далее мы повторим процесс с дополнительными данными и перепишем код, используя NumPy.

Получить данные

первый,нуждаться Получить данные。

import requests
import pandas as pd
import io

url = "https://raw.githubusercontent.com/brmson/dataset-sts/master/data/sts/sick2014/SICK_train.txt"

text = requests.get(url).text

data = pd.read_csv(io.StringIO(text), sep='\t')
data.head()

def build_shingles(sentence: str, k: int):
   shingles = []
   for i in range(len(sentence) - k):
       shingles.append(sentence[i:i+k])
   return set(shingles)

def build_vocab(shingle_sets: list):
   # convert list of shingle sets into single set
   full_set = {item for set_ in shingle_sets for item in set_}
   vocab = {}
   for i, shingle in enumerate(list(full_set)):
       vocab[shingle] = i
   return vocab

def one_hot(shingles: set, vocab: dict):
   vec = np.zeros(len(vocab))
   for shingle in shingles:
       idx = vocab[shingle]
       vec[idx] = 1
   return vec

k = 8  # shingle size

# build shingles
shingles = []
for sentence in sentences:
   shingles.append(build_shingles(sentence, k))

# build vocab
vocab = build_vocab(shingles)

# one-hot encode our shingles
shingles_1hot = []
for shingle_set in shingles:
   shingles_1hot.append(one_hot(shingle_set, vocab))
# stack into single numpy array
shingles_1hot = np.stack(shingles_1hot)
shingles_1hot.shape
# (4500, 36466)

Преобразование в горячее кодирование, shingles_1hot Массив содержит 500 разреженных векторов, длина каждого вектора равна размеру словаря.

MinHashing

Затем используйте минхеширование, чтобы сжать разреженный вектор в плотную векторную «подпись».

def minhash_arr(vocab: dict, resolution: int):
    length = len(vocab.keys())
    arr = np.zeros((resolution, length))
    for i in range(resolution):
        permutation = np.random.permutation(len(vocab)) + 1
        arr[i, :] = permutation.copy()
    return arr.astype(int)

def get_signature(minhash, vector):
    # get index locations of every 1 value in vector
    idx = np.nonzero(vector)[0].tolist()
    # use index locations to pull only +ve positions in minhash
    shingles = minhash[:, idx]
    # find minimum value in each hash vector
    signature = np.min(shingles, axis=1)
    return signature

arr = minhash_arr(vocab, 100)

signatures = []

for vector in shingles_1hot:
    signatures.append(get_signature(arr, vector))

# merge signatures into single array
signatures = np.stack(signatures)
signatures.shape
# (4500, 100)

Сократите разреженный вектор с длины до сигнатуры длиной 100. Хотя это сжатие существенно, оно хорошо сохраняет информацию о сходстве.

LSH

Здесь используется словарь Python для хэширования и хранения пар кандидатов:

from itertools import combinations

class LSH:
    buckets = []
    counter = 0
    def __init__(self, b):
        self.b = b
        for i in range(b):
            self.buckets.append({})

    def make_subvecs(self, signature):
        l = len(signature)
        assert l % self.b == 0
        r = int(l / self.b)
        # break signature into subvectors
        subvecs = []
        for i in range(0, l, r):
            subvecs.append(signature[i:i+r])
        return np.stack(subvecs)
    
    def add_hash(self, signature):
        subvecs = self.make_subvecs(signature).astype(str)
        for i, subvec in enumerate(subvecs):
            subvec = ','.join(subvec)
            if subvec not in self.buckets[i].keys():
                self.buckets[i][subvec] = []
            self.buckets[i][subvec].append(self.counter)
        self.counter += 1

    def check_candidates(self):
        candidates = []
        for bucket_band in self.buckets:
            keys = bucket_band.keys()
            for bucket in keys:
                hits = bucket_band[bucket]
                if len(hits) > 1:
                    candidates.extend(combinations(hits, 2))
        return set(candidates)
    
b = 20

lsh = LSH(b)

for signature in signatures:
    lsh.add_hash(signature)

lsh.buckets Содержит отдельный словарь для каждого бэнда, бакеты не смешиваются между разными бэндами. Храните векторы в ведрах ID (номер строки), поэтому при извлечении пар кандидатов просто перебирайте все сегменты и извлекайте пары.

candidate_pairs = lsh.check_candidates()
len(candidate_pairs)
# 7327

list(candidate_pairs)[:5]
# [(1063, 1582), (112, 1503), (114, 2393), (2685, 2686), (3197, 3198)]

После того как пары-кандидаты идентифицированы, расчеты сходства выполняются только для этих пар, и обнаруживается, что некоторые пары попадают в пределы порога сходства, а другие — нет.

Цель состоит в том, чтобы сузить область поиска и снизить сложность, сохраняя при этом высокую точность. Производительность можно визуализировать, измеряя классификацию пар кандидатов (1 или 0) по сравнению с фактическим сходством косинуса (или Жаккара).

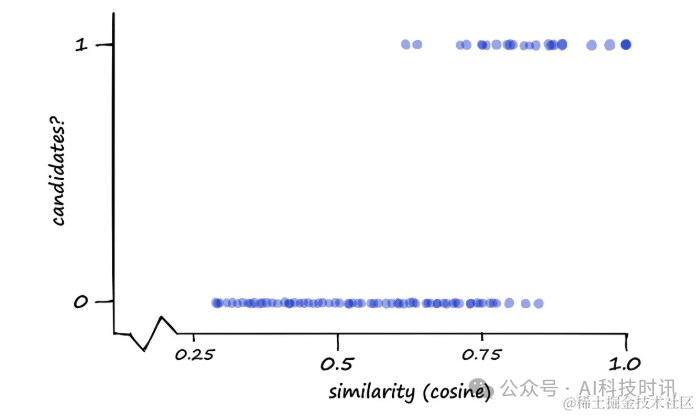
“Диаграмма, показывающая пары кандидатов（1）и пары некандидатов（0）Косинус относительно парной сигнатурысходствораспределение

Оптимизация значений полосы

В локально-чувствительном хешировании (LSH),стоимость полосыbявляется ключевым параметром,Определяет порог сходства,Прямо сейчасLSHфункция Границы, которые преобразуют точки данных из пар, не являющихся кандидатами, в пары-кандидаты.。корректируяb,Вы можете изменить чувствительность функции LSH.,Тем самым влияя на качество и скорость отзыва результатов поиска.

Связь между вероятностью и сходством можно формализовать следующим образом:

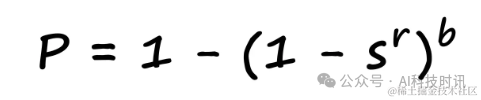
в,sвыражатьсходство Счет,bУказывает количество полос,rПредставляет количество строк в каждой полосе.。Эта формула помогает нам понять, что в данномbиrзаниженная стоимость,Вероятность того, что пара точек данных будет идентифицирована как пара-кандидат.

Визуализируя взаимосвязь вероятности и сходства, можно наблюдать четкую закономерность:

“

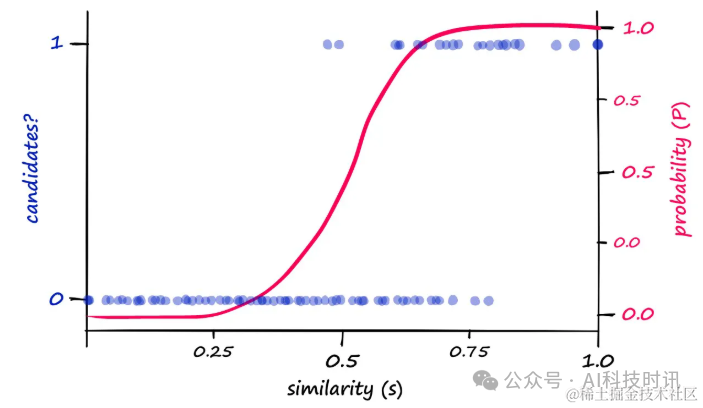
• Классификация кандидатов（левая сторонаyось）иРассчитанная вероятность P（правая сторонаyось）относительносходство（рассчитанный или нормированный косинуссходство）。
• существоватьbиrЦенности20и5случай,Вы можете увидеть Рассчитанную вероятность Значения P и сходства указывают на общее распределение пар кандидат/некандидат.

Хотя существует корреляция между теоретически рассчитанными вероятностями и реальными результатами пары кандидатов.,Но выравнивание не идеальное。путем измененияbценить,Вероятность возврата пары кандидатов с разными показателями сходства можно сдвинуть влево или вправо.

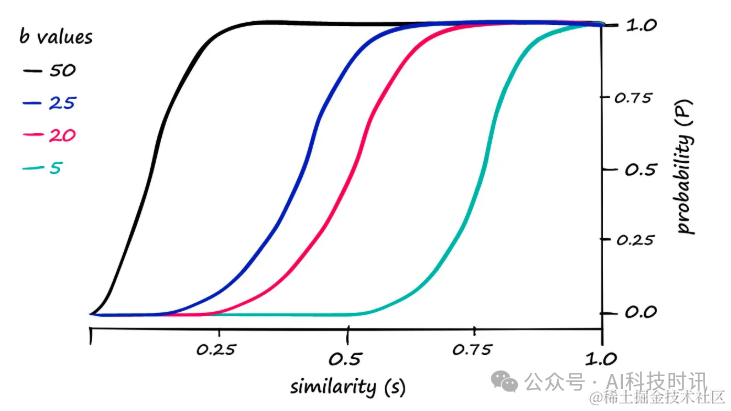
“Рассчитанная вероятность P против сходства для разных значений b. r - это лен (подпись) / б (в данном случае len(подпись) == 100）。

Например,Если найденb == 20час,Для того чтобы пара была рассчитана как пара-кандидат, требуется более высокое сходство.,Вы можете попробовать увеличитьbценитьуменьшитьсходствопорогценить。когдаbценить Отрегулируйте25час,Можно наблюдать следующие изменения:

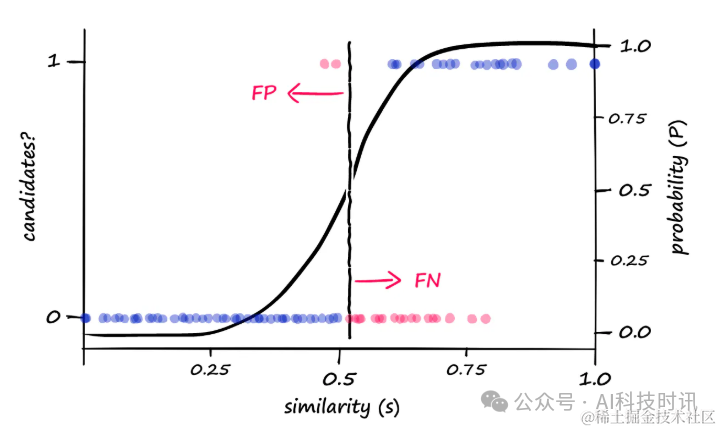
“когдаb == 25час,Реальные и смоделированные результаты показаны синим и пурпурным цветом соответственно. По сравнению с предыдущими результатами LSH,Увеличиватьbценитьв результате появляется больше пар кандидатов

Это приводит к большему количеству ложных срабатываний на разнородных векторах, поскольку возвращается больше пар кандидатов. Это можно визуализировать как:

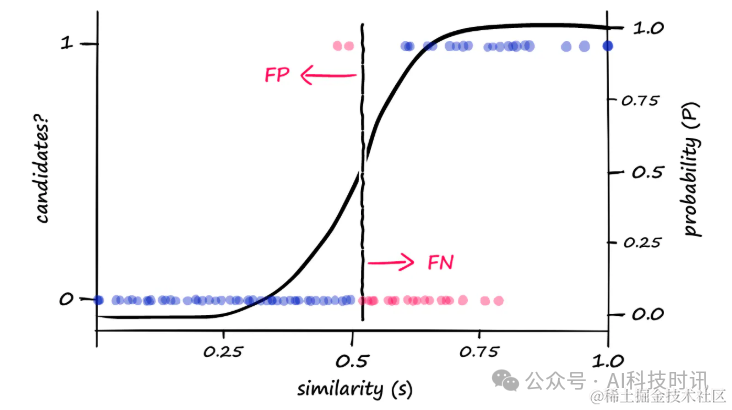
“Увеличиватьbценитьестественно приведет к тому, что будет возвращено больше пар кандидатов,Это может увеличить количество ложных срабатываний (FP).,при этом уменьшая количество ложноотрицательных результатов (FN)

Построив процесс LSH с нуля и отрегулировав порог сходства, можно оптимизировать качество и запоминаемость результатов поиска. В этой статье не только представлены основные принципы LSH, но также рассматриваются концепции шинлинга и функций MinHash. В практических приложениях мы можем реализовать LSH с использованием библиотеки, специально разработанной для поиска по сходству, чтобы повысить эффективность и точность.

Подвести итог

В этой статье представлена ​​технология локально-чувствительного хэширования (LSH).,Это ключевой метод достижения быстрого и точного поиска в сходствопоиске. LSH широко используется крупными технологическими компаниями, такими как Google и Netflix. В статье подробно рассматривается работа ЛШпринцип.,Включая шинлинг, MinHashing и Чередование и хеширование и другие шаги. с помощью этих технологий,LSH способен поддерживать скорость поиска, пока,Обеспечивает качественные результаты поиска. наконец,Демонстрация процесса реализации LSH на примерах Python,И обсудили, как оптимизировать порог сходства функции LSH, регулируя значение полосы.

ссылка

• https://youtu.be/e_SBq3s20M8
• locality-sensitive-hashing
• jupyter notebook
• Mining of Massive Datasets