Прогнозирование многомерных временных рядов всегда было постоянной проблемой, с которой сталкивались различные дисциплины. Данные временных рядов часто демонстрируют разнообразные внутри- и межрядные корреляции, которые приводят к сложным и переплетенным зависимостям и были в центре внимания многочисленных исследований.

Однако в понимании межрядных корреляций изменений в нескольких временных рядах в разных временных масштабах остаются значительные исследовательские пробелы, и этой области в литературе уделяется ограниченное внимание.

В этой статье представлен документ по многомерному прогнозированию временных рядов, совместно опубликованный Сычуаньским университетом, Гонконгским университетом науки и технологий и Пекинским технологическим институтом. В этой работе предлагается MSGNet, целью которого является фиксация изменения корреляций между последовательностями в нескольких временных масштабах с использованием анализа частотной области и адаптивной свертки графов, заполняя пробелы в вышеуказанной области.

Название статьи:MSGNet: Learning Multi-Scale Inter-Series Correlations for Multivariate Time Series Forecasting

Бумажный адрес:https://arxiv.org/abs/2401.00423

Исходный код бумаги:https://github.com/YoZhibo/MSGNet

Обзор бумаги

MSGNet — это усовершенствованная модель глубокого обучения, предназначенная для отслеживания изменения корреляций между последовательностями в нескольких временных масштабах с использованием анализа частотной области и адаптивной свертки графов. Используя анализ частотной области, MSGNet может эффективно извлекать важные периодические закономерности и разлагать временные ряды на различные временные масштабы.

Модель сочетает в себе механизм самообслуживания для фиксации внутрипоследовательных зависимостей, а также представляет адаптивный гибридный слой свертки с пропуском графа для автономного изучения различных корреляций между последовательностями в каждом временном масштабе. Кроме того, MSGNet также имеет возможность автоматически изучать интерпретируемые многомасштабные корреляции между последовательностями, демонстрируя сильные возможности обобщения даже при применении к выборкам вне распределения.

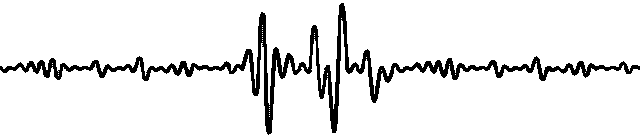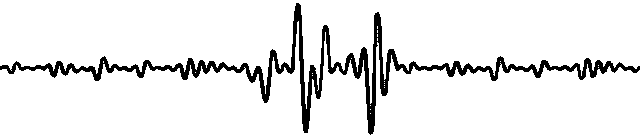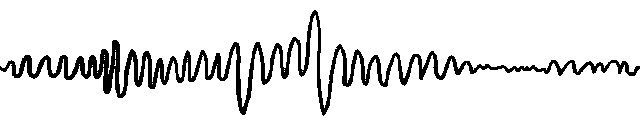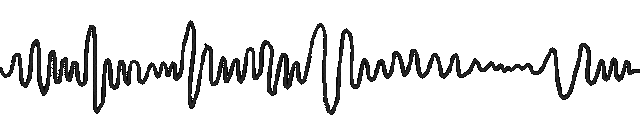
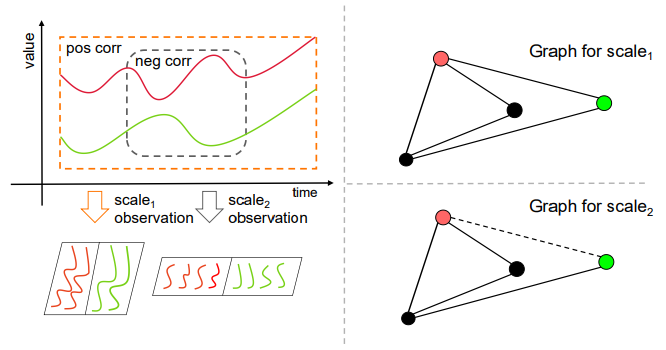
Подводить итоги,Долженбумага Основная отправная точка заключается в том, что：Отношения между несколькими переменными являются многомасштабными.。В качестве примера исследователь берет следующий рисунок.,где на шкале времени 1,Мы можем наблюдать положительную корреляцию между двумя временными рядами.,И в более коротком масштабе времени 2,Мы можем заметить отрицательную корреляцию между ними. С помощью методов, основанных на графах, получаются две разные структуры графов. поэтому,Внедрение MSGNet и его применение для анализа временных рядов,Особенно при выявлении корреляций между меняющимися рядами в разных временных масштабах.,Оно открывает новые пути решения важных проблем в этой области.

модельная основа

Общая архитектура модели MSGNet показана на рисунке ниже. MSGNet состоит из нескольких модулей ScaleGraph, и его суть заключается в способности плавно интегрировать различные компоненты.

Каждый модуль ScaleGraph состоит из четырех шагов:

1. Определить масштаб входного временного ряда;

2. Используйте модуль адаптивной свертки графов для выявления масштабно-зависимых межпоследовательных корреляций;

3. Уловить внутрипоследовательную корреляцию посредством внимания нескольких голов;

4. Используйте функцию SoftMax для адаптивного агрегирования представлений разных масштабов.

Такое сочетание многомасштабного обучения и свертки графиков MSGNet позволяет модели более полно понимать данные временных рядов и точно прогнозировать будущие тенденции. Кроме того, введение многоголового внимания еще больше повышает способность модели улавливать сложные закономерности внутри последовательностей.

01

Input Embedding and Residual Connection

Эта часть в основном относится к таким работам, как Informer. Входные данные представляют собой в основном одномерную свертку исходной входной последовательности, а также внедрение позиции и времени.

Здесь ScaleGraphBlock представляет операции и вычисления, которые формируют основные функции уровня MSGNet.

02

Scale Identification

Исследователи стремятся повысить точность прогнозов, используя межрядные корреляции в разных временных масштабах. Выбор масштаба является ключом к этому модельному методу, поэтому исследователь использует периодичность в качестве источника масштаба.

Вдохновленные TimesNet, исследователи используют быстрое преобразование Фурье (БПФ) для обнаружения заметной периодичности как шкалы времени, чтобы более точно фиксировать периодические закономерности в данных временных рядов. Сопоставьте временной ряд с частотной областью и найдите основную частоту topK как масштаб.

03

Multi-scale Adaptive Graph Convolution

Мы предлагаем новый метод свертки многомасштабных графов для выявления конкретных и всеобъемлющих зависимостей между последовательностями. Для этого тензор, соответствующий i-му масштабу, сначала перепроецируется на тензор с N переменными посредством линейного преобразования, где N представляет собой количество временных рядов. Эта проекция осуществляется посредством линейного преобразования, определяемого следующим образом:

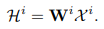
в,

,

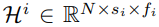
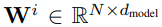
— это обучаемая весовая матрица, настроенная для тензора i-го масштаба. Можно опасаться, что корреляция между последовательностями может измениться после применения линейного картирования и последующего линейного картирования. Однако комплексные эксперименты исследователей показывают, что с помощью метода свертки графов предлагаемый метод может умело сохранять корреляции между последовательностями.

04

Multi-head Attention and Scale Aggregation

В каждом временном масштабе исследователи используют Multi-Head Attention (MHA) для выявления внутрипоследовательных корреляций. Используя преобразование масштаба для преобразования длительных временных интервалов в периодические, решается вопрос эффективности MHA в улавливании долгосрочных временных корреляций во временных рядах.

05

Output Layer

Чтобы делать прогнозы, модель использует линейные проекции как во времени, так и в переменных измерениях. Таким образом, модель способна улавливать сложные закономерности в данных временных рядов и сопоставлять эти закономерности с будущими моментами времени посредством линейной проекции. Это позволяет MSGNet эффективно выполнять долгосрочные и краткосрочные прогнозы и подходит для различных задач прогнозирования временных рядов, таких как прогноз погоды, прогноз цен на акции и т. д.

Результаты эксперимента

В этой работе были проведены эксперименты с 8 наборами данных, а именно: «Полет», «Погода», «ETT» (h1, h2, m1, m2), «Курс валют» и «Электричество».

В частности, с точки зрения среднеквадратической ошибки (MSE) для разных длин прогноза MSGNet достигла наилучшей производительности на 5 наборах данных и второй лучшей производительности на 2 наборах данных. В наборе данных Flight MSGNet превосходит лучшую на данный момент модель TimesNet, при этом средние MSE и MAE снизились на 21,5% (с 0,265 до 0,208) и 13,7% (с 0,372 до 0,321) соответственно.

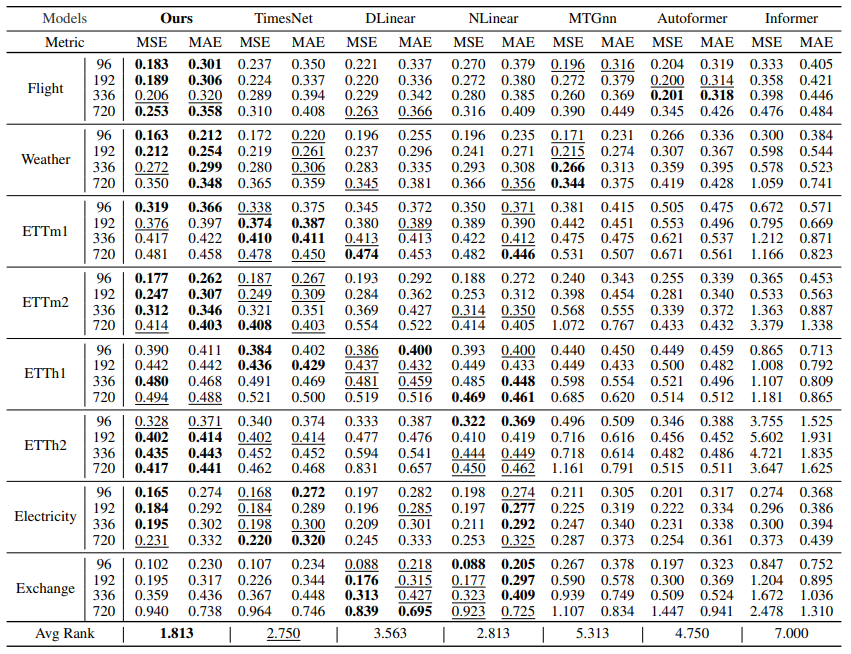
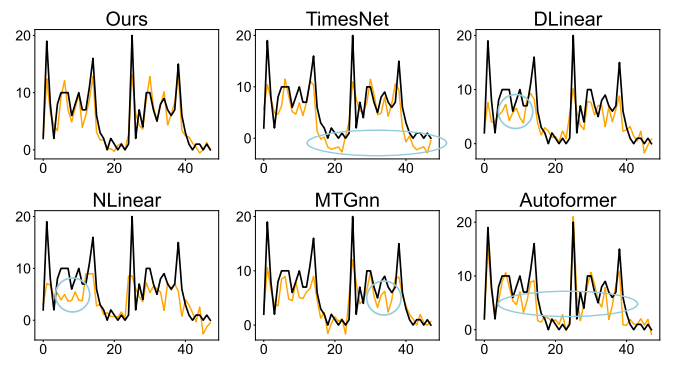
На рисунке ниже представлена ​​визуализация результатов прогнозирования полета. MSGNet точно отражает реальную ситуацию, в то время как другие модели демонстрируют очевидное снижение производительности в определенные периоды времени. Пики и спады на графике соответствуют ключевым событиям, тенденциям или циклической динамике полетных данных. Другие модели не могут точно отслеживать эти изменения, возможно, из-за архитектурных ограничений, которые ограничивают их способность улавливать многомасштабные закономерности, внезапные изменения или сложные меж- и внутрипоследовательные корреляции.