Оглавление

упрощение формулы

Упрощение логической функции для указанного устройства

Минимальный срок

определение

природа

Редактировать

Максимальный срок

определение

природа

отношения между двумя

“Минимальный форма "сумма срока"

“Максимальный форма продукта "срок"

каноту

определение

Пример

Редактировать Функции

каноту представление логической функции

базовыйприрода

Матч 2 к 1

Матч 4 и 2

Матч 8 к 3

вывод

Основные шаги для упрощения

Общие правила

Пример

Ограничения

определение

любой предмет

определение

нерелевантные предметы

определение

приложение

Метод Q——M

упрощение формулы

        Давайте введем упрощение Формула, в основном включает в себя 5 методов, давайте познакомим их один за другим!

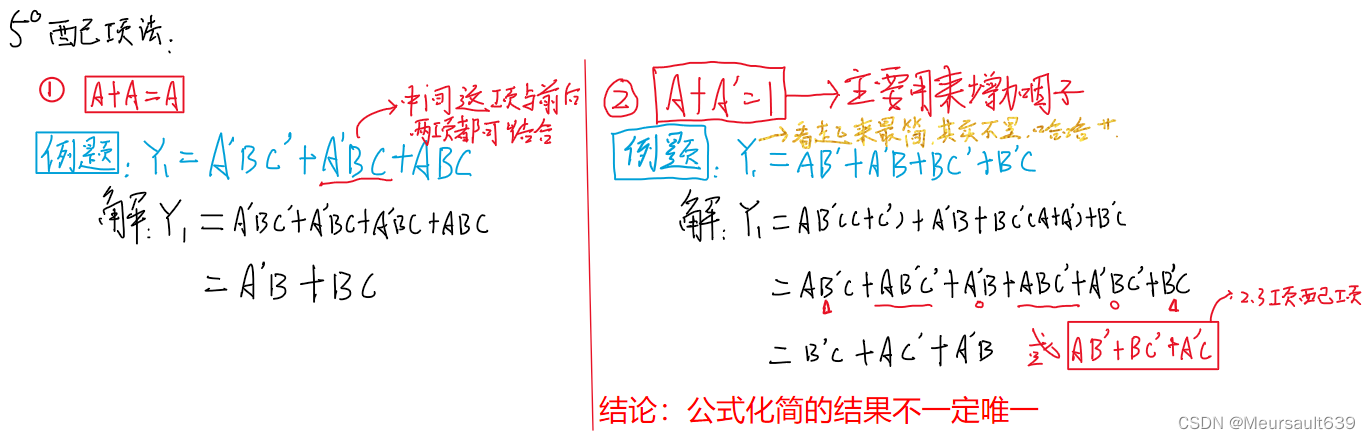
​ ​ ​ Далее давайте подведем итог этим пяти методам! 

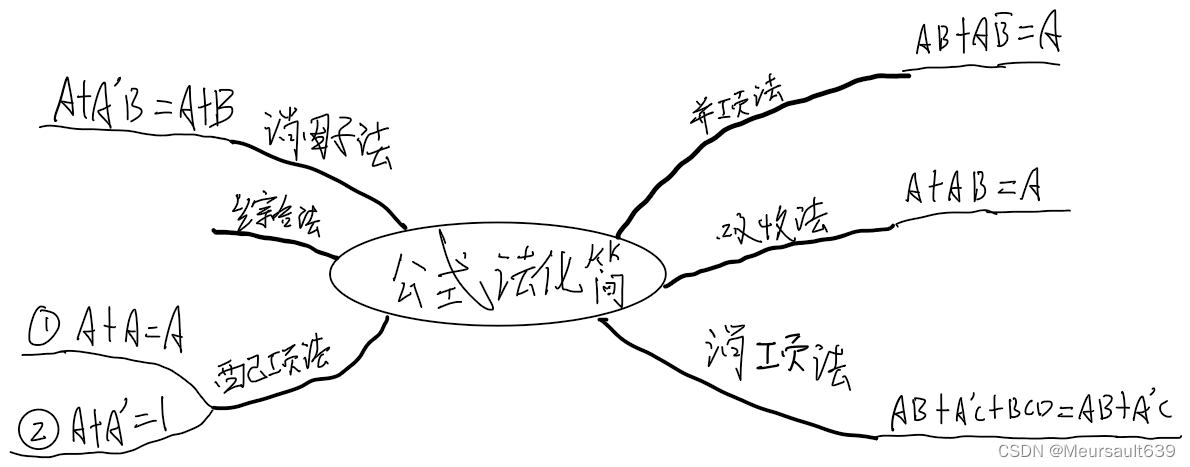
Наконец, давайте представим комплексный метод, который объединяет пять вышеуказанных методов и основную теорему!

Упрощение логической функции для указанного устройства

Минимальный срок

определение

природа

Максимальный срок

определение

природа

отношения между двумя

На самом деле это взаимоисключающие отношения, и то же самое происходит и в дискретной математике.

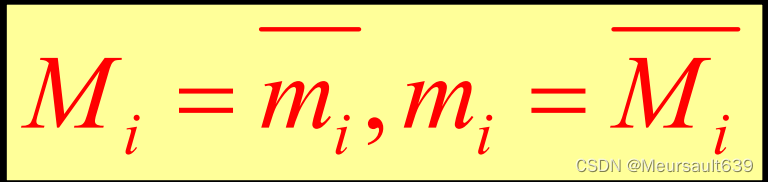
“Минимальный форма "сумма срока"

        логическая функция“Минимальный срок Нова”форма,также называется стандартным “И-ИЛИ”выражение。         Используйте основные формулы A+ A' = 1,Любую логическую функцию можно преобразовать в Минимальную. Стандартная форма суммы срока. Эта стандартная форма получила широкое распространение при упрощении логических функций, а также в компьютерном анализе и проектировании.

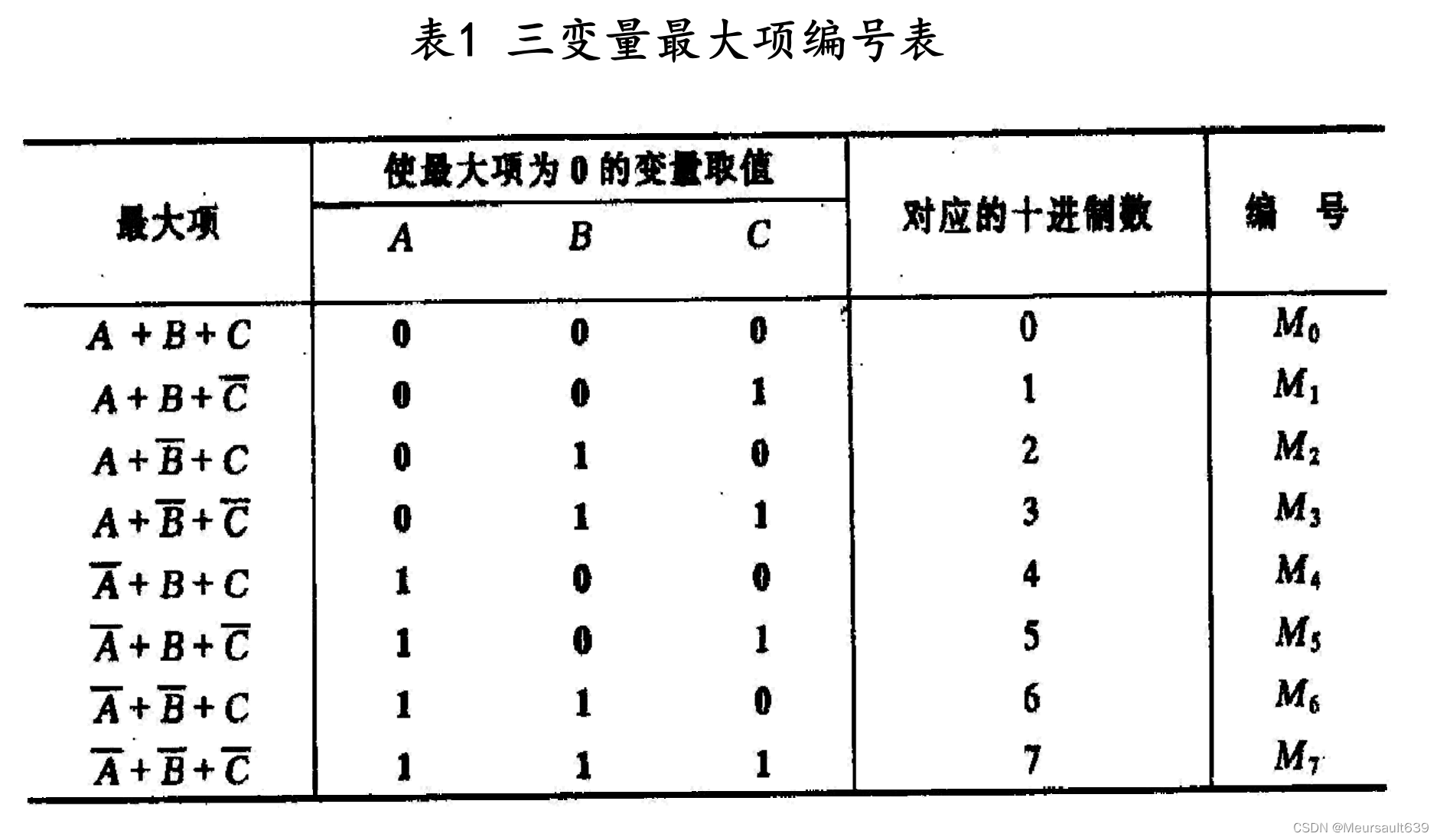
“Максимальный форма продукта "срок"

        логическая функция“Максимальный срокпродукт”форма,также называется стандартным“или-с”выражение。

        И мы рассчитываем Максимальный При расчете произведения срока обычно сначала рассчитывается Минимальный. Сумма срока конвертируется в Максимальный. Произведение срока выглядит следующим образом:

каноту

определение

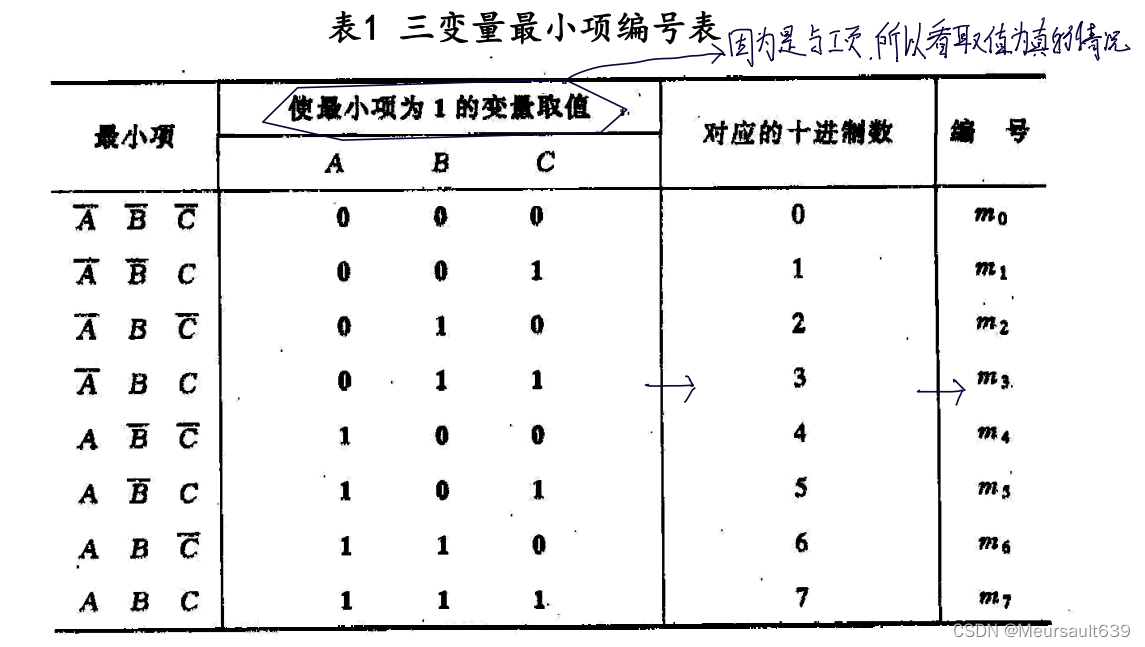
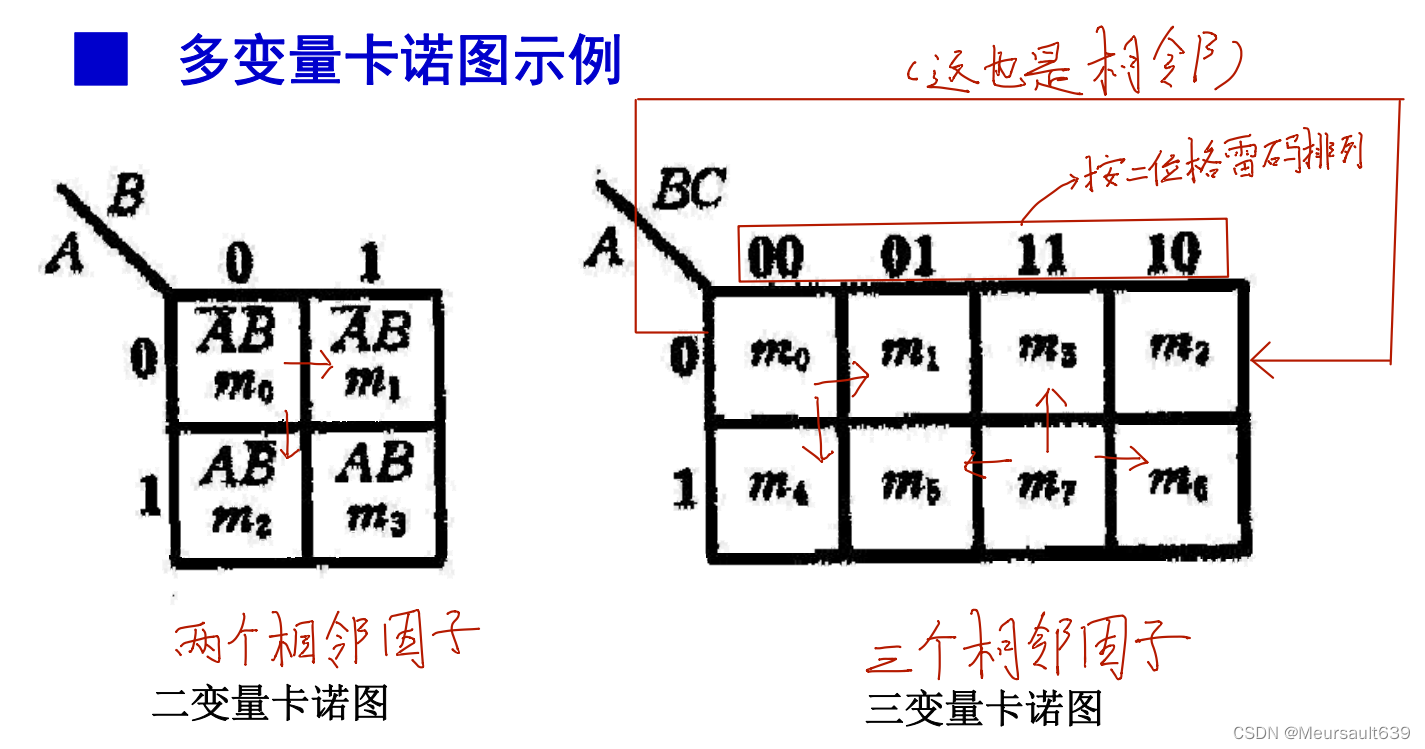
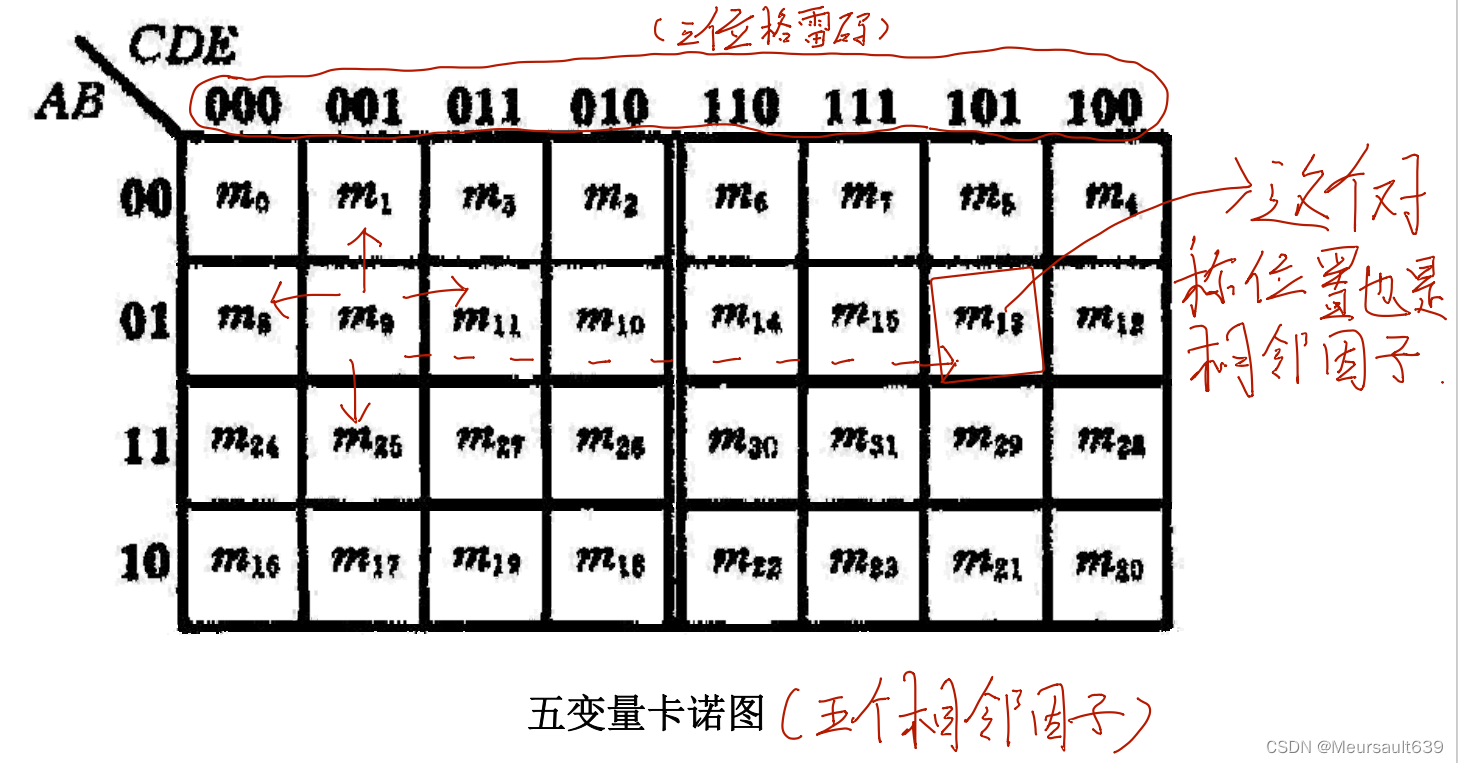
        каноту（Karnaugh Map) —— Это Юми Китайский инженер Карно впервые предложил метод описания логики. Специальная сетка функций.         ★ На этой сетке каждый маленький квадрат представляет собой один Минимальный логических функций срок；         ★ А геометрически соседние квадратики соседствуют логически. Природа, то есть Минимальный, представленный двумя соседними квадратиками. Есть только один Переменные имеют разные значения.

Пример

Функции

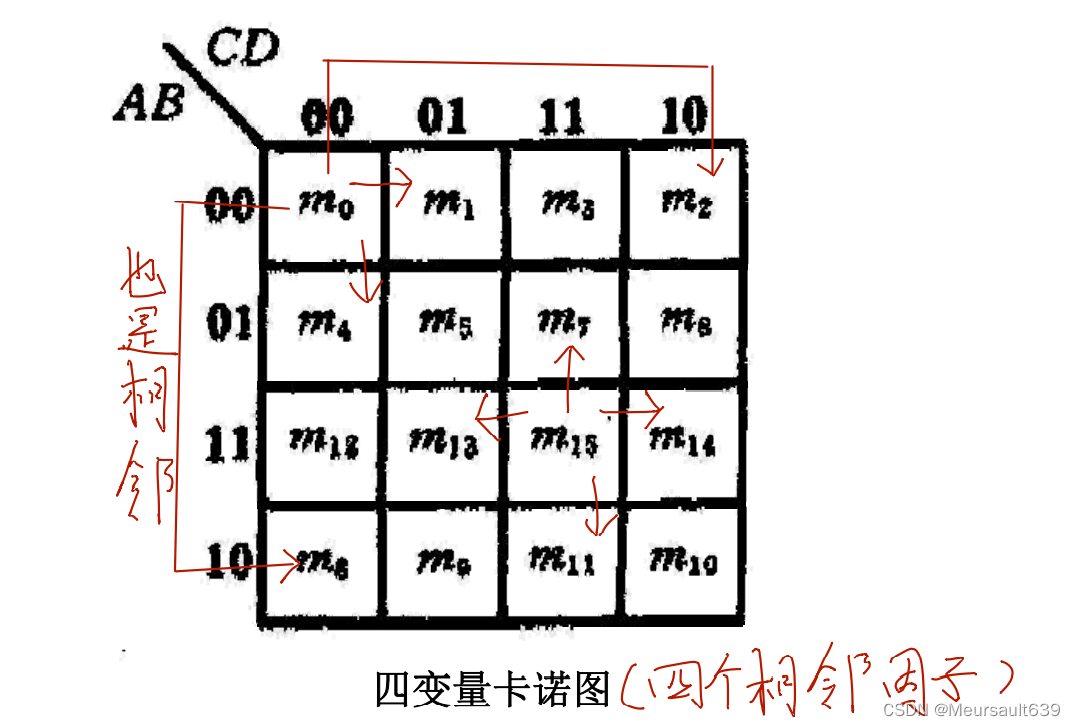
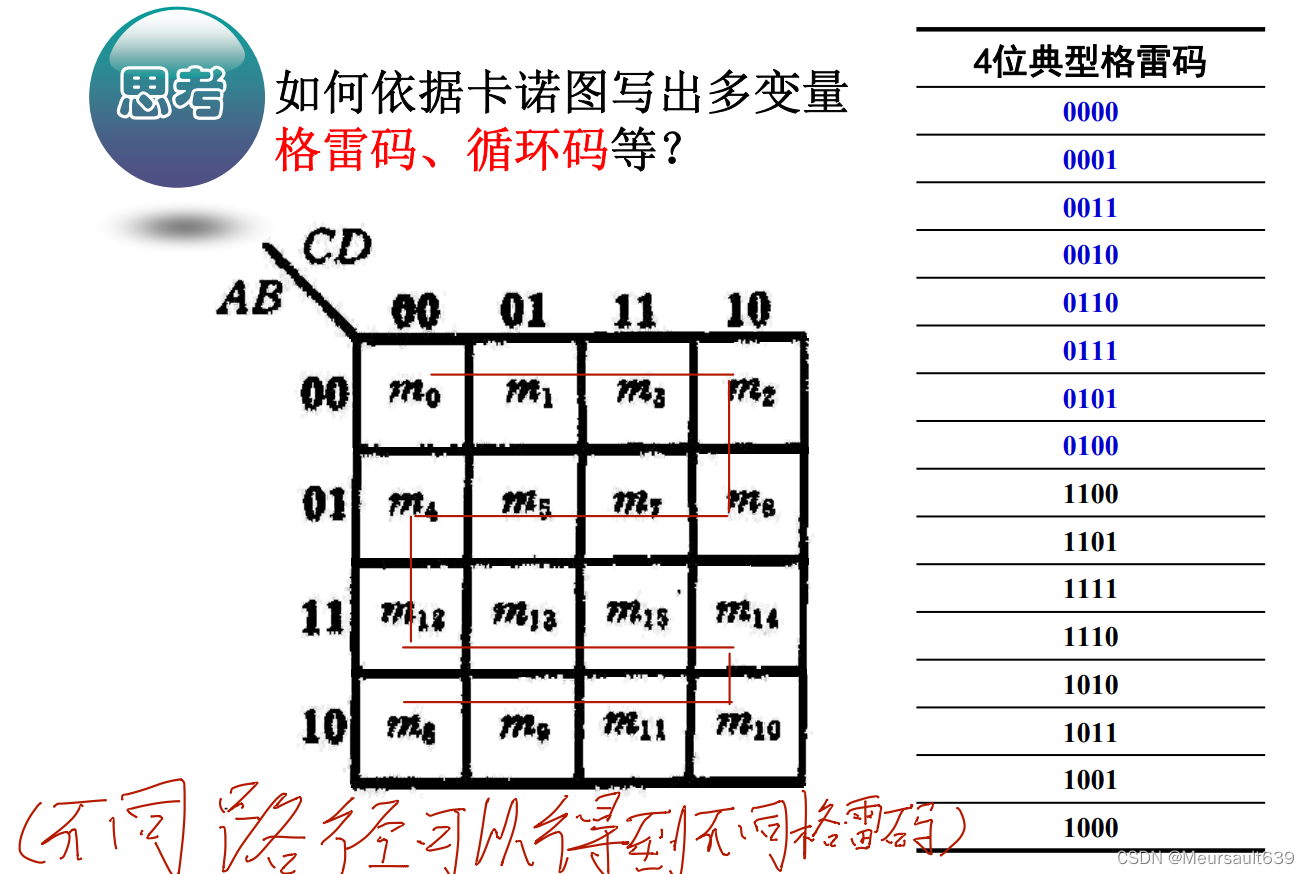
        Количество маленьких квадратов в ◆каноту равно Минимальному. Общее количество сроков, если количество переменных логической функции равно n, то количество маленьких квадратов равно 2^n индивидуальный.         ◆каноту Цифры 0 и 1, отмеченные с обеих сторон строки и столбца, означают, что Минимальный в соответствующем квадрате Значение переменной срок равно 1. В то же время размер этих двоичных чисел, составленных из 0 и 1, соответствует Минимальному. Число сроков. Кроме того, в каноту геометрически примыкает Минимальный срок имеет логическую смежность,поэтому,Значения переменных нельзя расположить в порядке двоичных чисел.,Необходимо нажатьциклический коддоговоренность。         ◆каноту — это замкнутая фигура из единицы вверх и вниз, влево и вправо, то есть соседствуют не только квадраты, находящиеся рядом друг с другом, но и соответствующие квадраты вверх и вниз, влево и вправо. 

каноту представление логической функции

Шаги по рисованию логической функции каноту

1. Известная функциональная формула
2. в суммарную форму Минимального срока
3. канотусредняя переписка Минимальный срок Заполните поле“1”
4. получить каноту

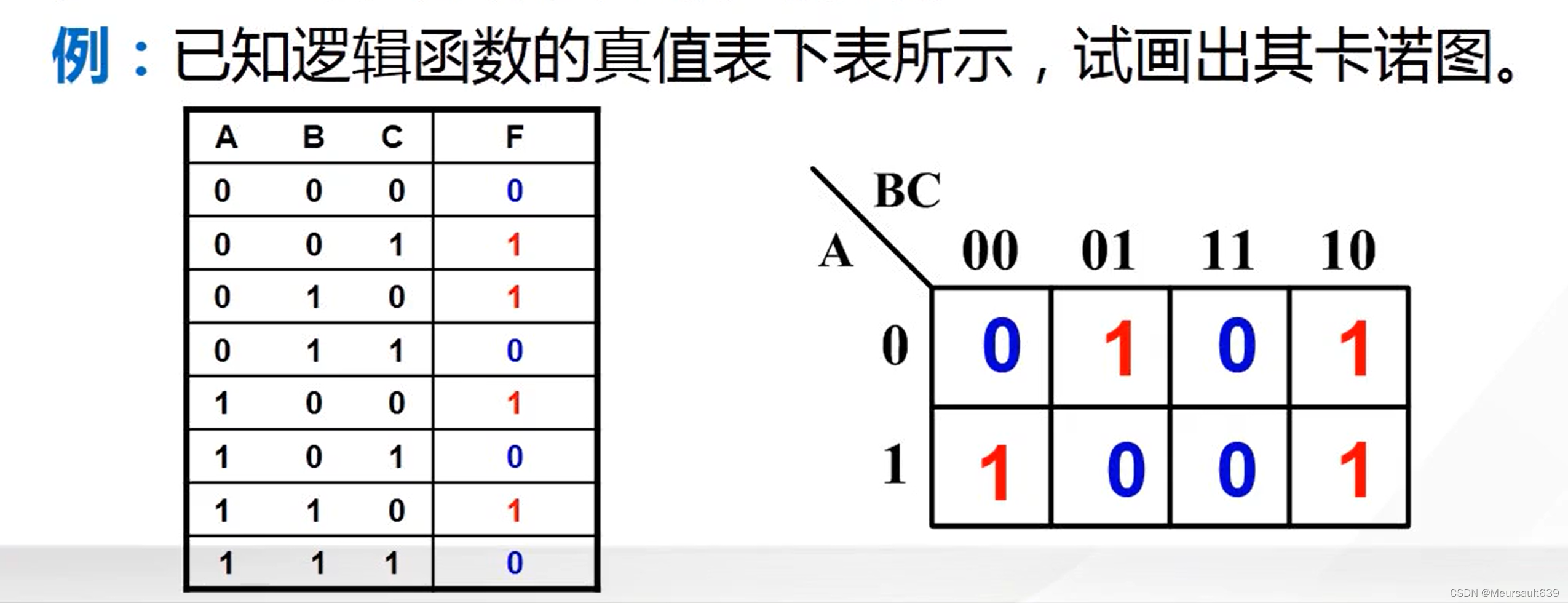
известная таблица истинностирисованиеканоту

1. известная таблица истинности
2. Значение функции, соответствующее каждому набору переменных (т. е. Минимальный срок).
3. Заполните соответствующие поля в каноту

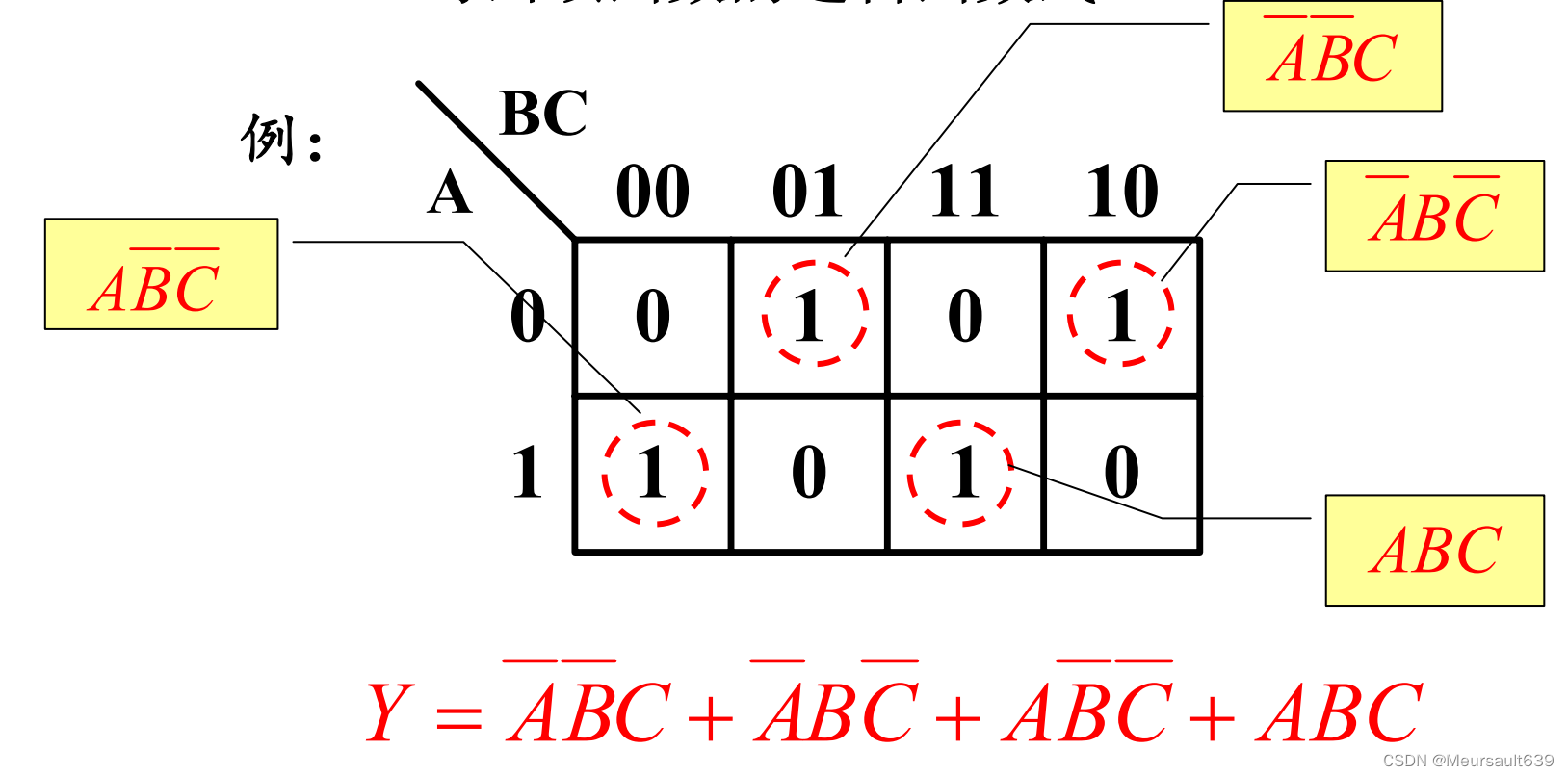
Напишите выражение каноту, учитывая логическую функцию

1. Таблица истинности функции (необязательно)
2. Напишите логическое выражение функции

базовыйприрода

Матч 2 к 1

         природа1：канотусерединаДве соседние ячейки «1»из Минимальный срок можно объединить Чэнодин и Сян,и устранитьодинпеременная。

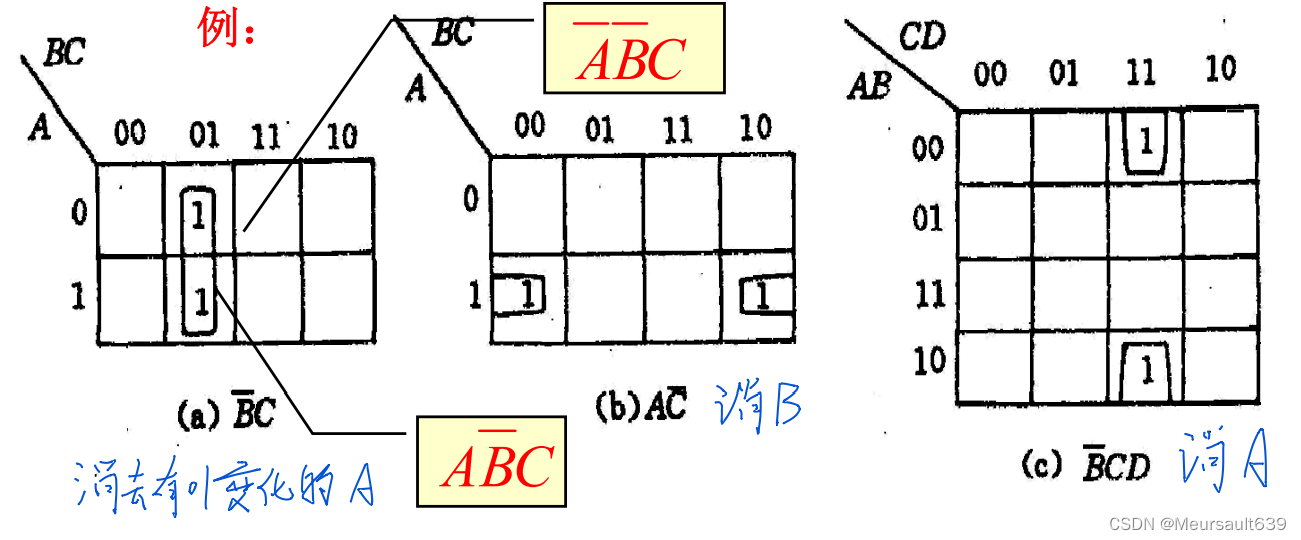
Матч 4 и 2

        природа2：канотусерединаЧетыре соседние ячейки «1»из Минимальный срок можно объединитьстановиться одини предметы,и устранитьдвапеременная。

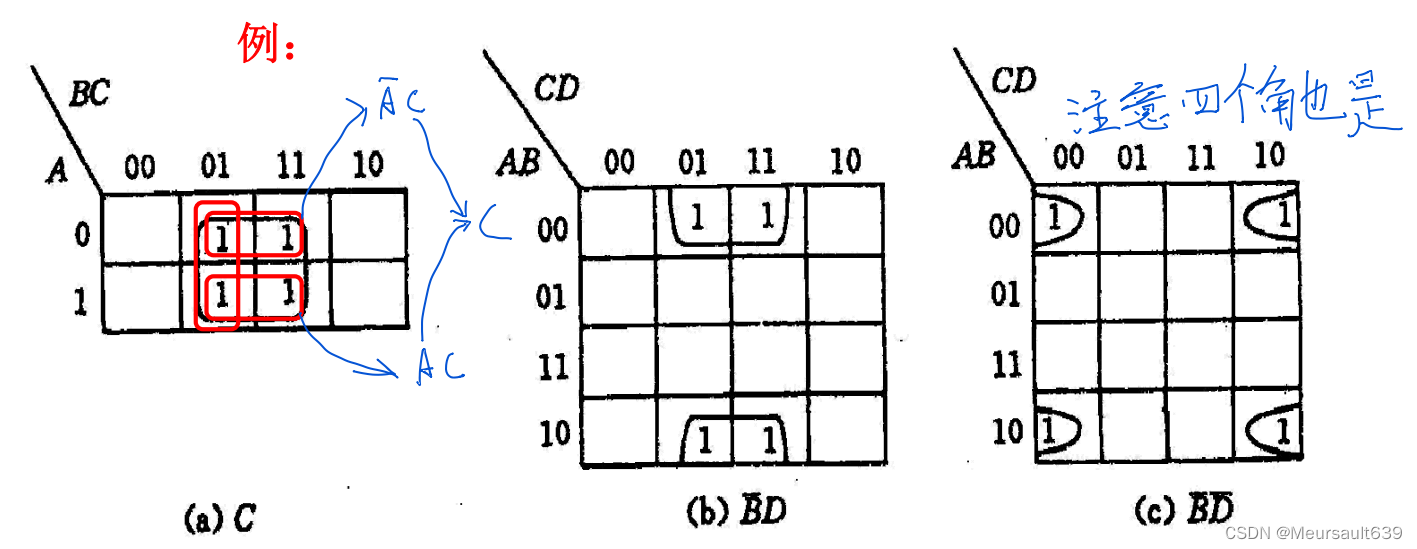
Матч 8 к 3

        природа3：канотусерединаВосемь соседних ячеек «1»из Минимальный срок можно объединить Чэнодин и Сян,и устранитьтрипеременная。

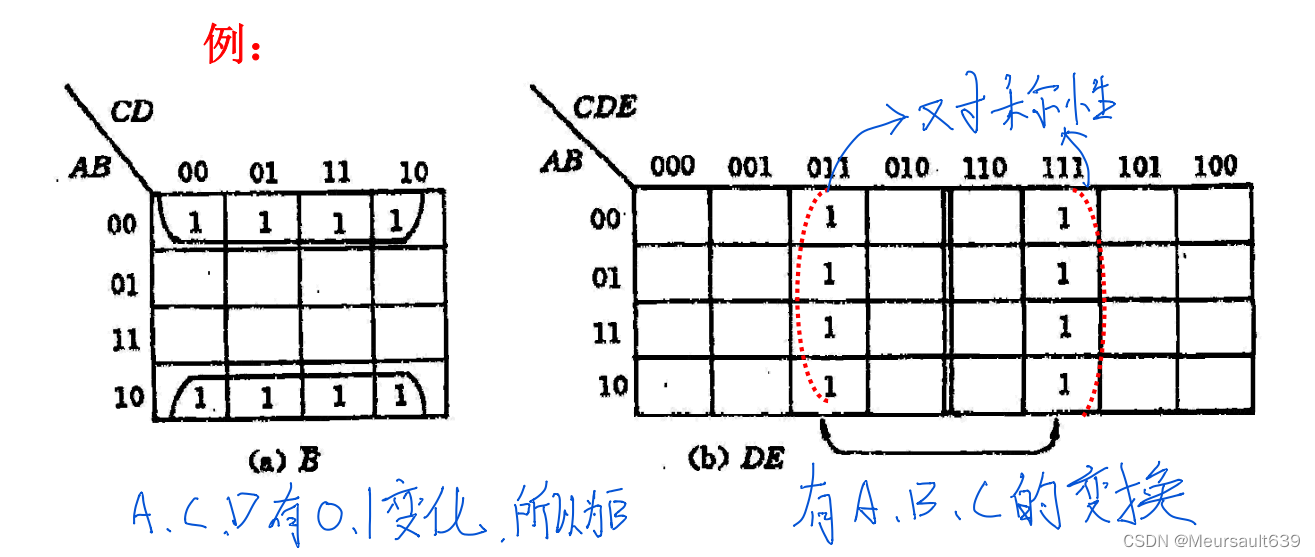
вывод

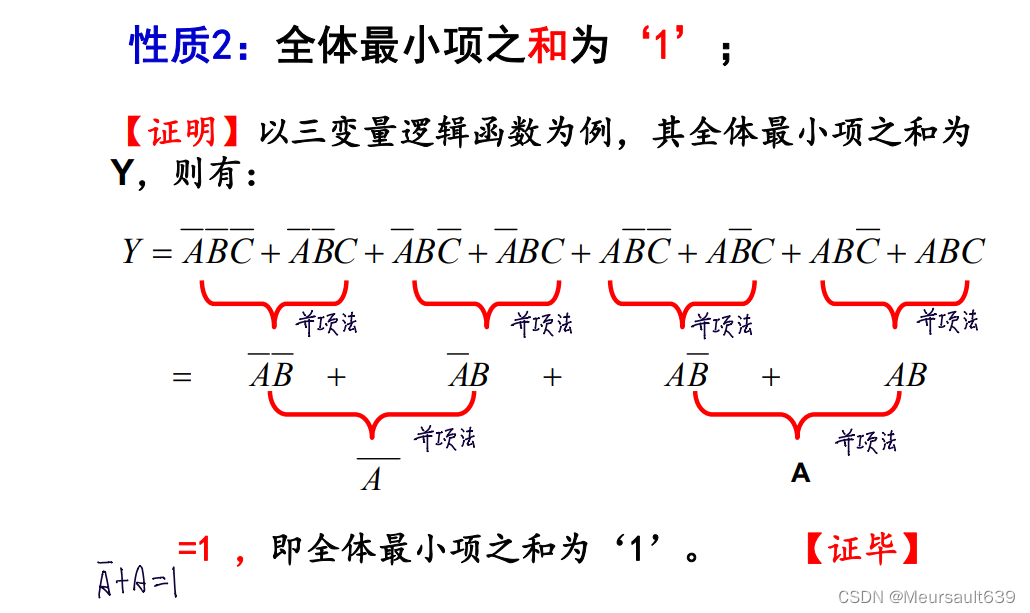
        В каноту из n переменных, если имеется 2^k "1" ячеек, смежных друг с другом (k=0, 1, 2, 3,..., n), их можно обвести и объединить, а k можно быть исключены при слиянии. Различные переменные упрощаются до единиц и членов с (n-k) переменными.         Если k=n, все переменные можно исключить при слиянии, и результат будет равен 1. Потому что Минимальный Сумма срока равна 1. 

Основные шаги для упрощения

1. Получите таблицу истинности функции или преобразуйте функцию в минимальную. сумма срока стандартная форма;
2. Нарисуйте каноту функции;
3. слить Минимальный срок (т.е. «нарисовать круг»);

Правила «Круга»:

• «1» квадрат один тоже нельзя пропустить,В противном случае выражение не равно функции;
• Квадрат «1» можно окружить кружками выше единицы, потому что A+A=A;
• Число кругов должно быть как можно меньшим, поскольку один круг соответствует одному и сроку, то есть с наименьшим сроком;

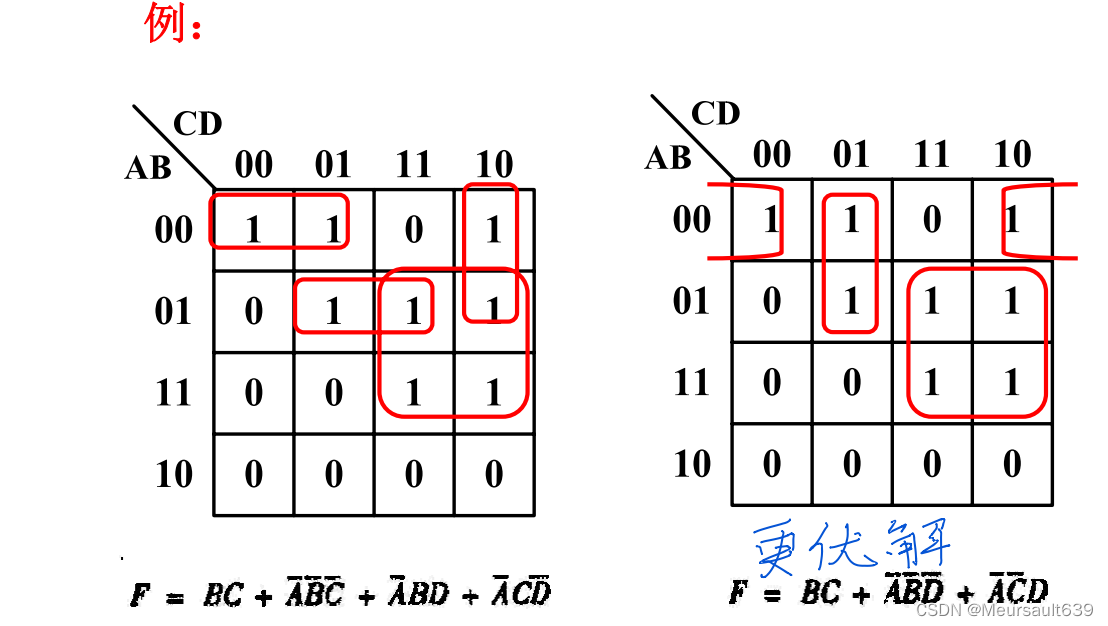
• Чем больше площадь круга, тем лучше, но она должна быть 2к квадратов. Это связано с тем, что чем больше круг, тем больше переменных исключено и тем меньше переменных содержится в термине И.

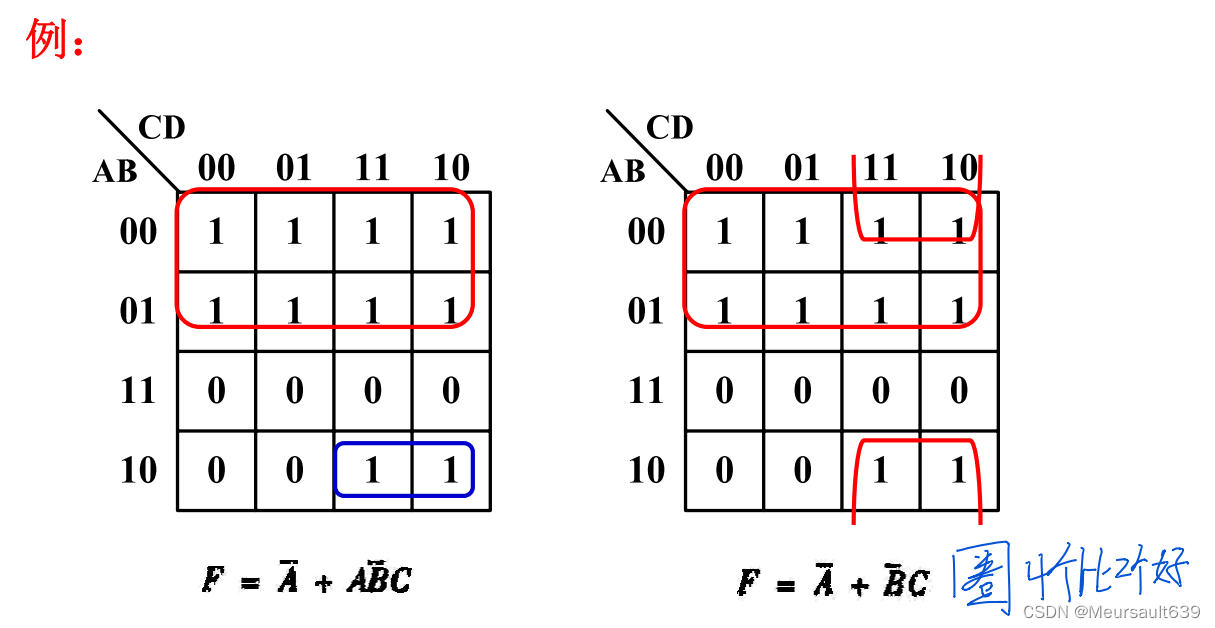
• Каждый круг должен содержать как минимум новую ячейку «1».,В противном случае этот круг лишний,То есть добавляются лишние элементы;

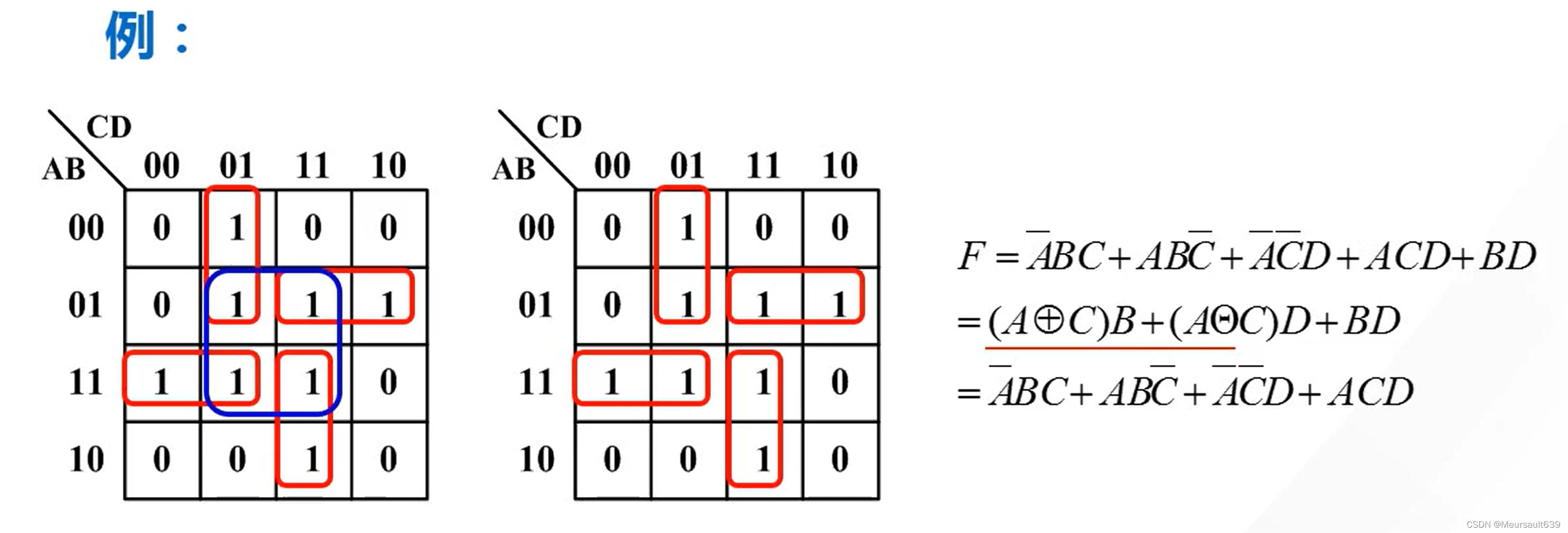
BD этого вопроса, то есть средний кружок избыточен. 

Общие правила

«Его можно перерисовать, но нельзя пропустить. Количество кругов должно быть небольшим, площадь круга должна быть большой, и каждый круг должен иметь новую цифру «1».

Пример

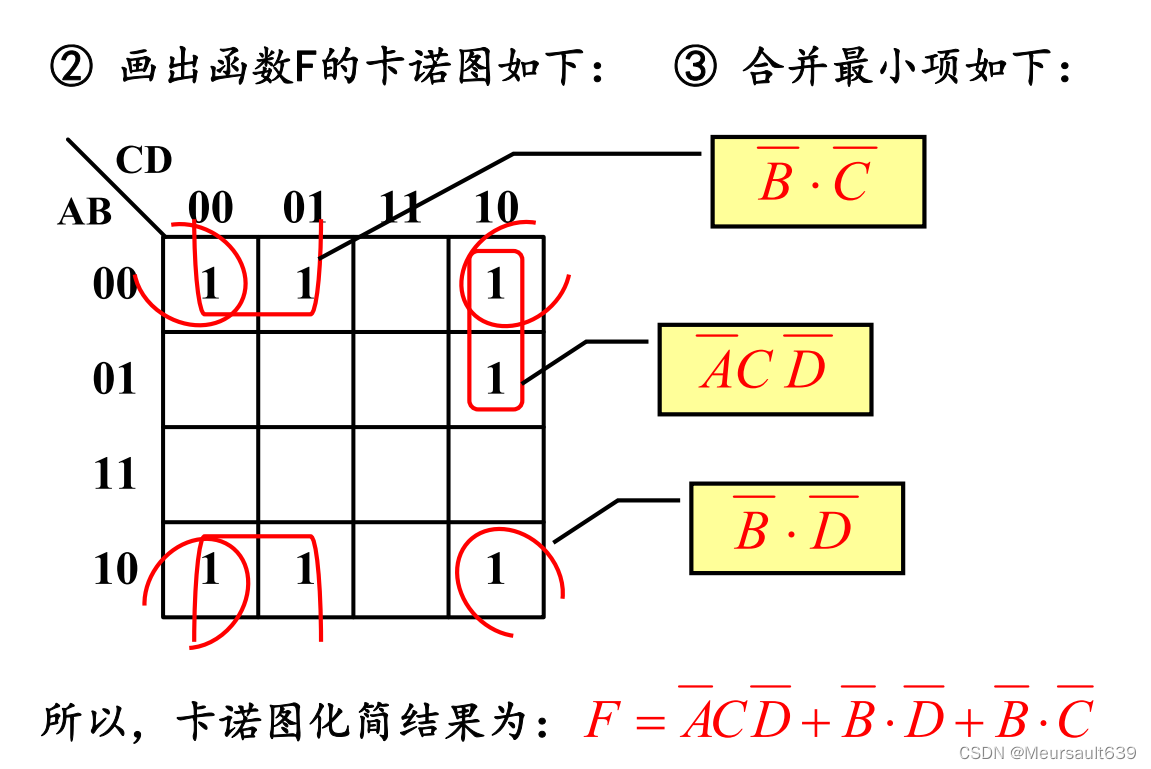
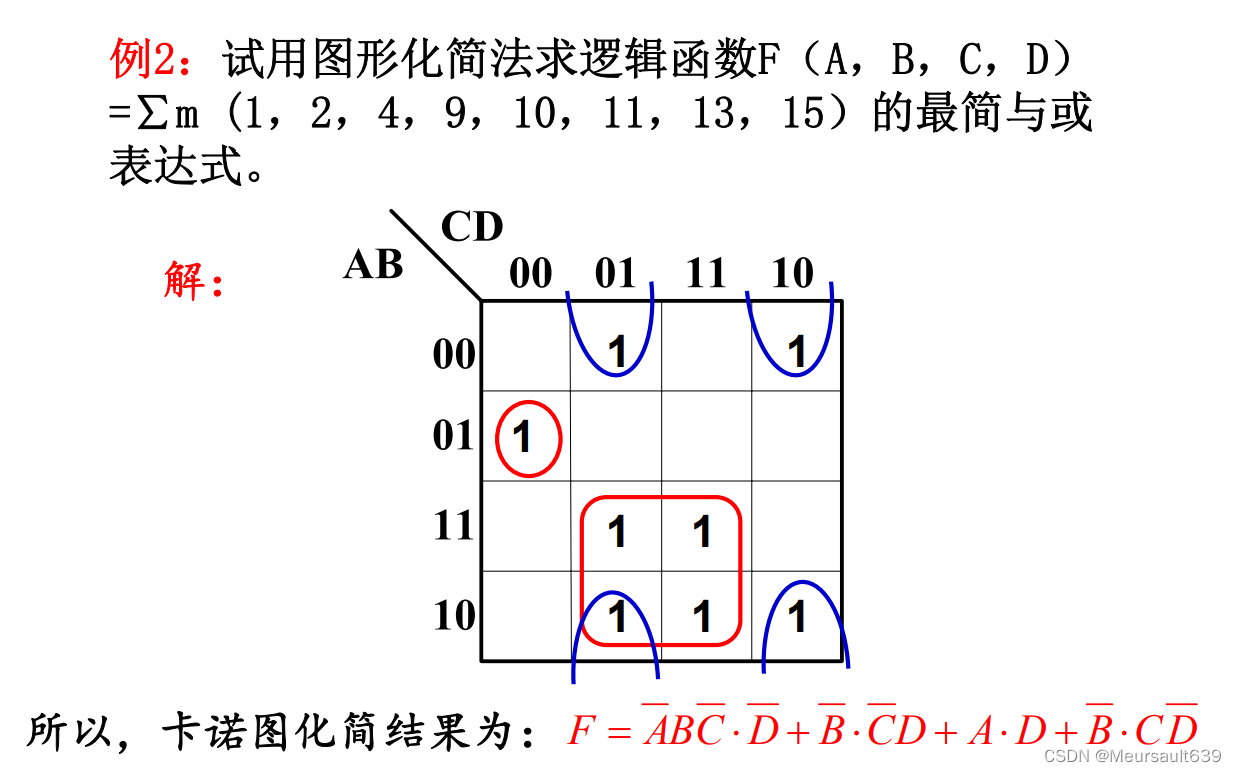
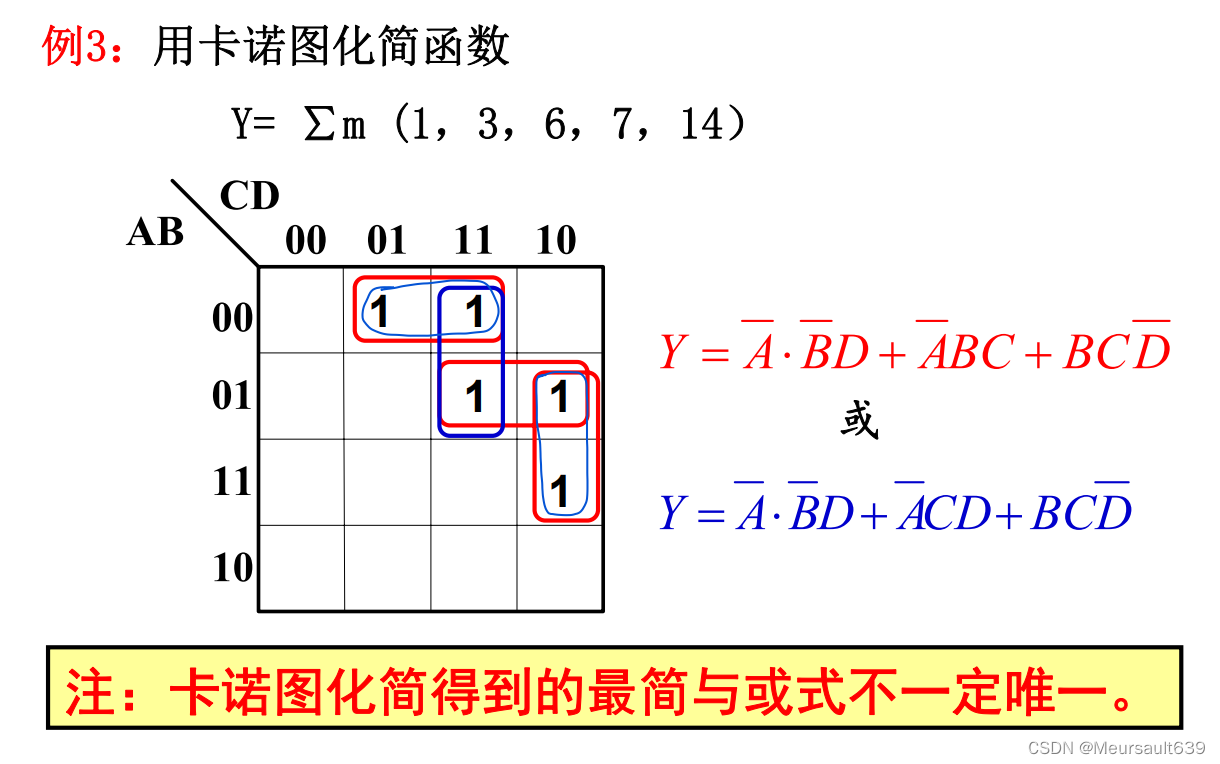
Ограничения

определение

 Ограничения——в некоторых случаях,входитьпеременнаяиз Значение не является произвольным из. Их можно использовать при ограничении появления значений определенных входных переменных. переписыватьсяиз Минимальный срок всегда равен 0. Эти Минимальные равны 0 срокпозвонить по поводу Объединить предметы.

любой предмет

определение

 любой предмет——有时входитьпеременнаяиз Некоторые значения1все еще 0 допустимо и не влияет на работу схемы. Принимайте значения в этих переменных Ниже представлены те Минимальные, значение которых равно 1. срокназываетсялюбой предмет。

нерелевантные предметы

определение

        нерелевантные предметы——Ограниченияилюбой предмет, известный под общим названием «нерелевантные» в логических функциях предметы. «Нерелевантно» относится к тому, являются ли эти Минимальные срок Написание логических функциональных выражений не имеет значения,в канотуиспользовать“×”выражатьнерелевантные предметы。При упрощении логической функции ее можно считать равной 1 или 0.

приложение

        Упрощайте с помощью нерелевантных При использовании логических функций предметов, если вы можете разумно ими воспользоваться нерелевантные предметов, как правило, можно получить более простые результаты упрощения.         слить Минимальный Когда срок, знак «×» в каноту следует считать 1 или 0? Получившийся соседний Минимальный срок Прямоугольная комбинация является наибольшей, а количество прямоугольных комбинаций равно Минимум – это принцип.

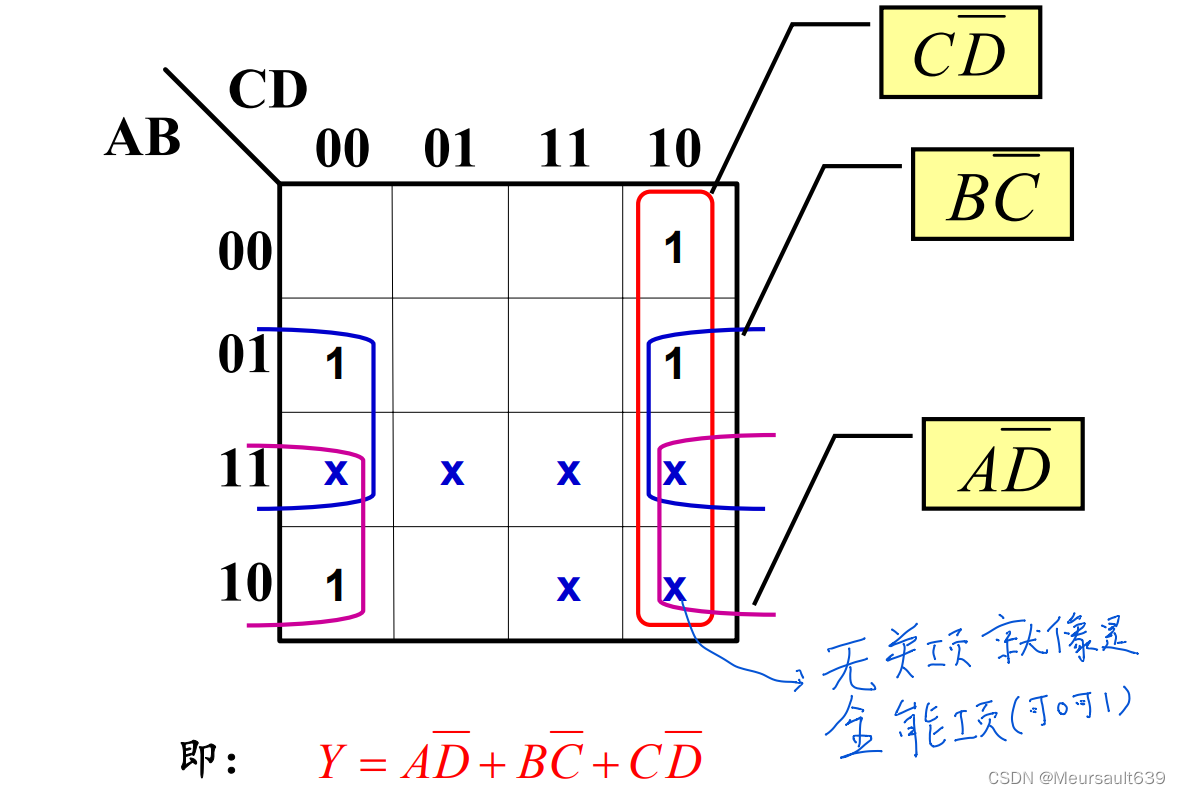
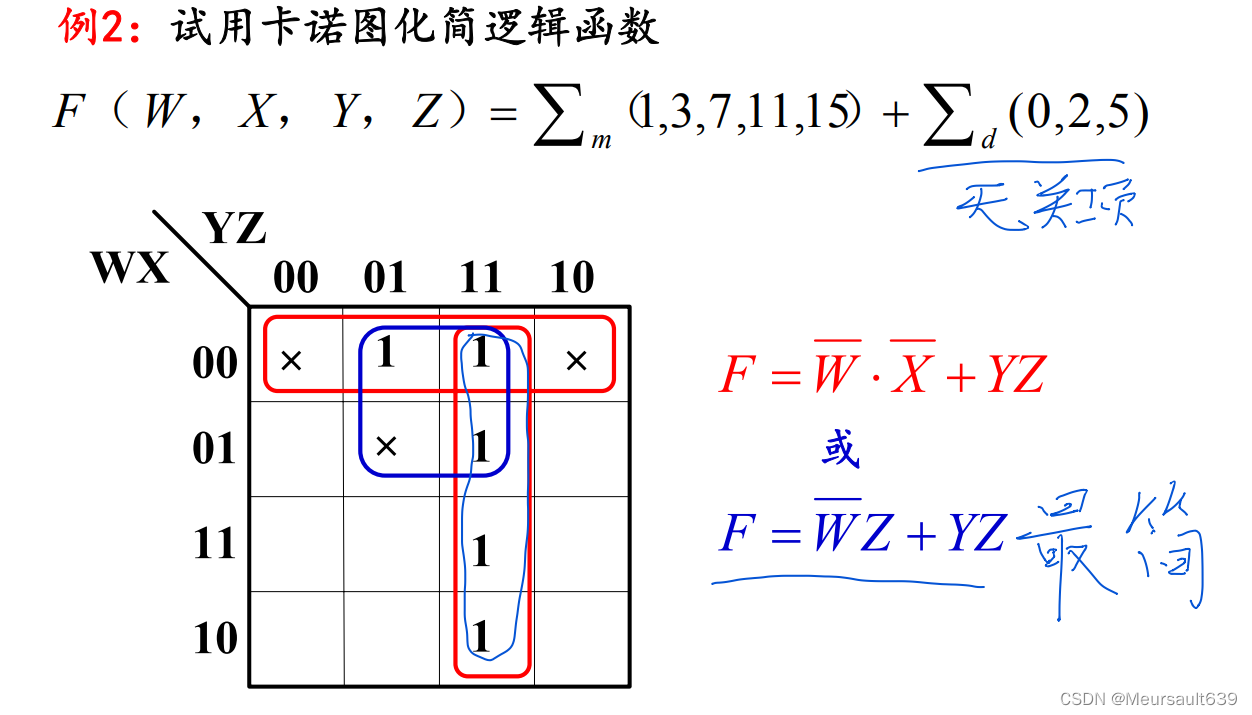
        В принципе, есть два решения этого примера. Все решения верны, но по «простейшему» принципу только одно. Это решение является самым простым и желательным. Поэтому при рассмотрении каноту Упрощая неединственность, следует также учитывать принцип «минимума».

Метод Q——M

Его еще называют упрощенным методом Куинна-Микласки, потому что в средней школе по дискретной математике выпускной экзамен тоже является экзаменом! Я не буду вдаваться в подробности. Заинтересованные студенты могут убедиться в этом сами!